2014-09-14
ロトカ=ヴォルテラの向きの分離

my.Moving.Frame.2 <- function(X,k=length(X[1,])){
	n <- length(X[,1]) # No. points
	d <- length(X[1,]) # Dimension
	# inter-point distance
	L <- rep(0,n-1)
	for(i in 1:(n-1)){
		L[i] <- sqrt(sum((X[i,]-X[i+1,])^2))
	}
	diff.X <- list()
	#diff.X[[1]] <- X
	diff.X[[1]] <- apply(X,2,diff)
	diff.L <- list()
	diff.L[[1]] <- L
	for(i in 2:k){
		diff.X[[i]] <- apply(diff.X[[i-1]],2,diff)
		tmp.n.pt <- length(diff.X[[i]][,1])
		tmp.L <- rep(0,tmp.n.pt-1)
		for(j in 1:(tmp.n.pt-1)){
			tmp.L[j] <- sqrt(sum((diff.X[[i]][j,]-diff.X[[i]][j+1,])^2))
		}
		diff.L[[i]] <- tmp.L
	}
	mf <- list() # Moving Frame
	mf[[2]] <- diff.X[[2]]/sqrt(apply(diff.X[[2]]^2,1,sum))
	if(k>2){
		for(i in 3:k){
			n.pt <- length(diff.X[[i]][,1])
			ip <- apply(diff.X[[i]] * mf[[i-1]][1:n.pt,],1,sum)
			mf[[i]] <- diff.X[[i]] - ip * mf[[i-1]][1:n.pt,]
			mf[[i]] <- mf[[i]]/sqrt(apply(mf[[i]]^2,1,sum))
		}
	}
	n.pt <- length(diff.X[[k]][,1])
	mf[[1]] <- matrix(0,n.pt,d)
	for(i in 1:n.pt){
		tmp.mat <- matrix(0,d-1,d-1)
		tmp.vec <- rep(0,d-1)
		for(j in 2:d){
			tmp <- mf[[j]][i,]
			tmp.mat[j-1,] <- tmp[1:(d-1)]
			tmp.vec[j-1] <- tmp[d]
		}
		mf[[1]][i,] <- c(-solve(tmp.mat) %*% tmp.vec,1)
	}
	mf[[1]] <- mf[[1]]/sqrt(apply(mf[[1]]^2,1,sum))
	
	Cs <- matrix(0,d-1,length(diff.L[[1]]))
	for(i in 1:(d-1)){
		n.pt <- length(diff.L[[i+1]])
		Cs[i,1:n.pt] <- diff.L[[i+1]][1:n.pt]/L[1:n.pt]
	}
	mf.array <- diff.array <- array(0,c(n,k,k))
	for(i in 1:k){
		tmp.n <- length(mf[[i]][,1])
		delta.n <- n-tmp.n
		init.n <- ceiling(delta.n/2)
		if(init.n==0)init.n <- 1
		r.id <- init.n:(init.n+tmp.n-1)
		mf.array[r.id,i,] <- mf[[i]]
		
		tmp.n <- length(diff.X[[i]][,1])
		delta.n <- n-tmp.n
		init.n <- ceiling(delta.n/2)
		if(init.n==0)init.n <- 1
		r.id <- init.n:(init.n+tmp.n-1)
		diff.array[r.id,i,] <- diff.X[[i]]
	}
	
	return(list(L=L,mf=mf,mf.array=mf.array,diff.X=diff.X,diff.array=diff.array,diff.L=diff.L,Cs=Cs))
}
library(deSolve)
# 微分方程式
# この関数my.ODEに 引数 t は使われていないが
# runge-kuttaの本体関数 rk() との関係で、この引数は必要(らしい)
# 時刻を表す引数
# xは対象となっている変数の値のベクトル
# parmsは微分方程式の係数
# 差分を計算して返す
# この連立微分方程式はロトカ=ヴォルテラ
# parms[1],parms[4]は負、parms[2],parms[3]は正
my.ODE <- function(t, x, parms)  {

	dX <- (parms[1] + parms[2]*x[2])*x[1]
	dY <- (parms[3] + parms[4]*x[1])*x[2]

	res <- c(dX, dY)
	list(res)

}


## The parameters 
# 連立微分方程式の４係数を決める
# ２タイプあって、回転方向が逆
library(MCMCpack)
n <- 2
A1 <- rdirichlet(1,rep(1,4))*5
A1[c(1,4)] <- -A1[c(1,4)]
#A2 <- rdirichlet(1,rep(1,4))*5
#A2[c(1,4)] <- -A2[c(1,4)]
A2 <- -A1 + rnorm(4)*0.01
## vector of timesteps
# 計算する時刻
times <- seq(0, 10, length = 1001)

## 初期値
# 固定点の周囲から始まるとうまく周期性を出すので
# 固定点に若干のずれを入れる

N <- 100
X <- list()
dets <- matrix(0,length(times),N)
types <- c()
for(i in 1:N){


## Euler method
# hini 計算するための時間差分
if(runif(1)<0.5){
	xstart <- c(-A1[3]/A1[4], -A1[1]/A1[2]) + rnorm(2)*0.1

out1  <- rk(xstart, times, my.ODE, A1, hini = 0.1, method = "rk4")
types <- c(types,1)
}else{
	xstart <- c(-A2[3]/A2[4], -A2[1]/A2[2]) + rnorm(2)*0.1

out1  <- rk(xstart, times, my.ODE, A2, hini = 0.1, method = "rk4")
types <- c(types,2)
}
X[[i]] <- out1[,2:(n+1)]
mf1 <- my.Moving.Frame.2(X[[i]])
dets1 <- c()
for(ii in 1:length(mf1$diff.array[,1,1])){
	dets1 <- c(dets1,det(mf1$diff.array[ii,,]))
}

dets[,i] <- dets1
}
a <- which(types==1)[1]
b <- which(types==2)[1]
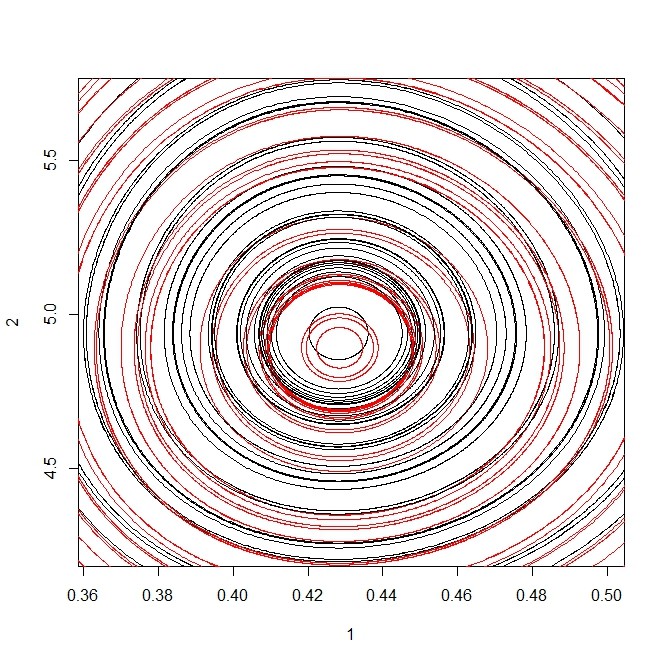
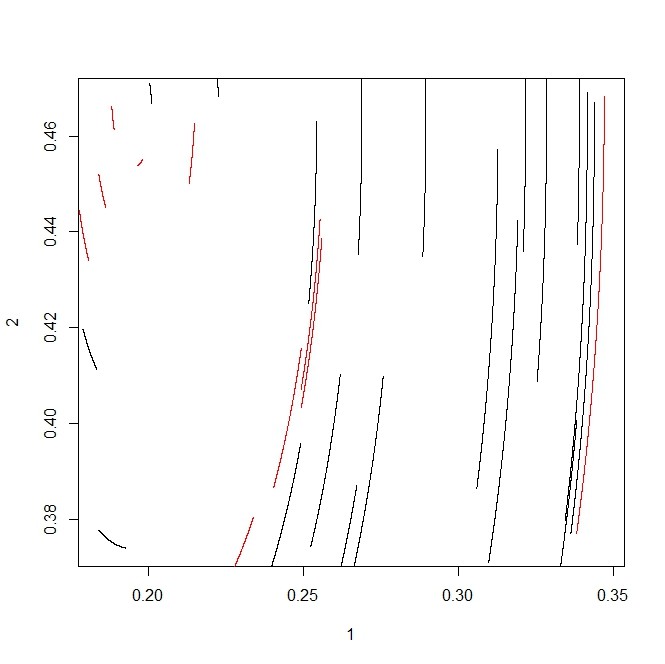
plot(X[[1]],type="l",xlim=range(c(X[[a]][,1],X[[b]][,1])),ylim=range(c(X[[a]][,2],X[[b]][,2])),col=types[1])
for(i in 2:N){
	lines(X[[i]],col=types[i])
}
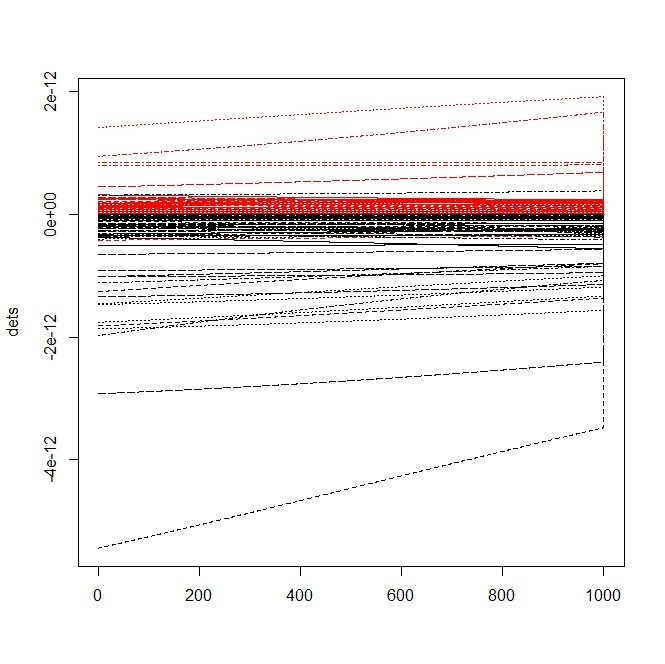
matplot(dets,type="l",col=types)