エッセンス：量子確率論 - ryamadaの遺伝学・遺伝統計学メモ

こちらで「量子確率論とその応用」をぱらぱらめくった
文書を抜き書きしただけで、特に数式についてはあえて端折った
この記事では、数式関連の抜き書きをする
直交多項式は以下のような漸化式で表される
- $P_0(x) = 1$
- $P_1(x) = x - \alpha_1$
- $P_{n+1}(x) = (x-\alpha_{n+1})P_n(x) + w_n P_{n-1}(x)$
ここで、 $\{\alpha_n\}_{n=1}^{\infty}, \{w_n\}_{n=1}^{\infty}\}, \alpha_n \in R, w_n \ge 0$ がヤコビ系数列
ヒルベルト空間の正規直交基底があって、それらは、３つの作用素によって以下のような関係にある
- $B^+ \Phi_n = \sqrt{w_{n+1}} \Phi_{n+1}$
- $B^- \Phi_0 = 0, \; B^- \Phi_n = \sqrt{w_n} \Phi_{n-1}$
- $B^o \Phi_0 = \alpha_{n+1} \Phi_n$
また、次のような関係がある
- $U : \Phi_n \to \frac{1}{\sqrt{\prod_{i=1}^n w_i}} P_n$
で、モーメントは
- $E(X^m) = \int_{-\infty}^{\infty} x^m \mu (dx)= < P_0, Q^m P_0 > = < \Phi_0, (B^+ + B^o + B^-)^m \Phi_0 >$
Rのorthopolynomパッケージを使うと、直交多項式が作れる

library(orthopolynom)
p.0 <- polynomial( c( 1 ) )
n <- 10
# ckpk+1 (x) = (dk + ekx) pk (x) − fkpk−1 (x)
# rec should specify ck,dk,ek and fk
# p_(n+1) = (x-alhap_n) p_n + w_(n-1) p_(n-1) が作りたい
rec <- data.frame(c=rep(1,n),d=-rnorm(n),e=rep(1,n),f=runif(n))
p.list <- orthonormal.polynomials( rec, p.0 )
p.list
x <- seq(from= -1,to=1,length=101)
ys <- polynomial.values(p.list,x)
ys.mat <- matrix(unlist(ys),ncol=length(p.list))
matplot(x,ys.mat,type="l")

f:id:ryamada22:20200502120320p:plain

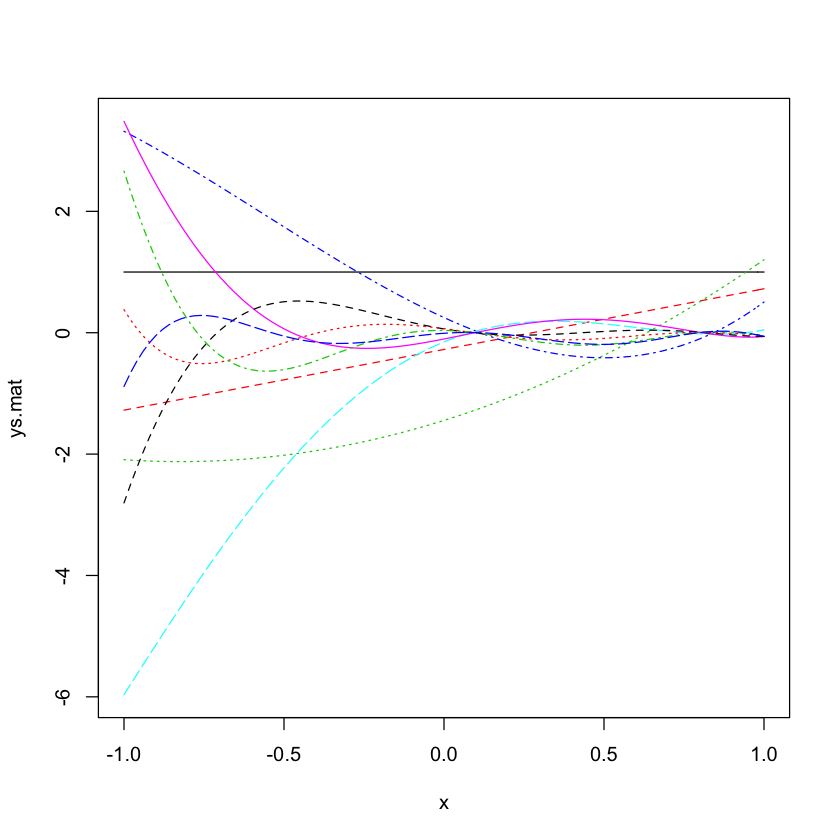
こんな問題設定
- ある関数V1とV2とがある
- 何かの拍子で、それらと正規直交基底のそれぞれとの内積がわかったとする
  - この２つの関数の正規直交基底との内積が、それぞれの「モーメント」から算出できるとき、それぞれのモーメント列がわかれば、その確率関数ペアの内積は求まりそうだ・・・
- その時、V1とV2との内積は $V1^T V2 = (V1^T R) (V2^T R)^T = V1^T R R^T V2 = V1^T I V2$ なので
- ちょっと有限次元でやっておく

d <- 3
R <- GPArotation::Random.Start(d)
V1 <- rnorm(d)
V2 <- rnorm(d)
sum(V1*V2)
IP1 <- matrix(V1,nrow=1) %*% R
IP2 <- matrix(V2,nrow=1) %*% R
sum(IP1 * IP2)

> sum(V1*V2)
[1] -1.460819
> IP1 <- matrix(V1,nrow=1) %*% R
> IP2 <- matrix(V2,nrow=1) %*% R
> sum(IP1 * IP2)
[1] -1.460819

より具体的には、区間を決めて、その範囲で定義した多項式を使う（ことが多い）。Legendre polynomialsはその一例