フェノタイプの整理メモ１８ 確率的に考える１４

• ネットワークに介入する(遺伝影響)
• 遺伝子多型などの影響は、因子(分子)の機能に多少の多寡が生じたり、ネットワークを通じて発現促進・抑制をする効率が変化したりする。これは、推移行列の値(微分方程式の係数)に違いをもたらす
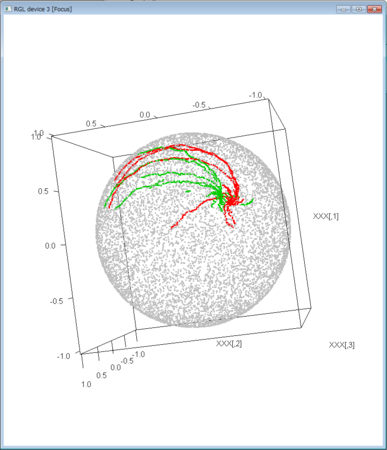
• 以下のソースでは、推移行列をわずかな角度で回転させ、推移行列に少しの違いを生じさせた上で、どのような状態変化が起きるかを示した
• 比較的安定しているときの複数因子の量の分布に違いがあるし、大きく揺らいだあとの、複数因子の収束の道筋が異なることもわかる

# 次元
n<-3
# 正規直交基底行列を作る
M<-Random.Start(n)
#M<-diag(n)
#M<-M[sample(1:n),]
# 繰返し数
Nrep<-4
# 繰返しごとのプロット数
Niter<-1000
plotstart<-1
commondrift<-0.005
raredrift<-0.1
rarefreq<-0.005

# プロットの角速度幅
dt<-0.01
dt2<-0.2
# x1=x2平面での回転行列
S<-diag(n)
S1<-matrix(c(cos(dt),sin(dt),-sin(dt),cos(dt)),2,2)
S[1:2,1:2]<-S1

# 遺伝子多型の保有具合の違いに応じて２つの推移行列を作る
SX1<-diag(n)
SR1<-matrix(c(cos(dt2),sin(dt2),-sin(dt2),cos(dt2)),2,2)
SX1[1:2,1:2]<-SR1

SR2<-matrix(c(cos(-dt2),sin(-dt2),-sin(-dt2),cos(-dt2)),2,2)
SX2<-diag(n)
SX2[1:2,1:2]<-SR2

M2<-M%*%SX2
M<-M%*%SX1


# 一つ目の推移行列でのシミュレーション
Xsum<-NULL
tmpcol<-c()
currentM<-diag(n)
for(ir in 1:Nrep){
	#currentM<-currentM%*%M

	# 座標
	X<-matrix(0,Niter,n)

	# 初期座標
	X[1,]<-runif(n)
	X[1,]<-X[1,]/sqrt(sum(X[1,]^2))
	# シミュレーション
	for(i in 2:Niter){
		P<-X[i-1,]
		Q<-M%*%P
		PQ<-Q-P
		# PとQを通る平面をx1=x2平面に移す行列
		R<-XYRotation(P,PQ)
		tmpP<-R%*%P
		tmpQ<-S%*%tmpP
		newQ<-solve(R)%*%tmpQ
		
		currentdrift<-commondrift
		if(runif(1)<rarefreq)currentdrift<-raredrift
		X[i,]<-newQ+rnorm(n)*currentdrift
		X[i,]<-X[i,]/sqrt(sum(X[i,]^2))
	}
	Xsum<-rbind(Xsum,X[plotstart:length(X[,1]),])
	tmpcol<-c(tmpcol,rep(ir,(Niter-plotstart+1)))
}

normX<-sqrt(sum(Xsum[1,]^2))

NrandPt<-10000
XX<-matrix(rnorm(NrandPt*n),NrandPt,n)
XX<-XX/sqrt(apply(XX^2,1,sum))*normX

XXX<-rbind(XX,Xsum)
col<-c(rep("gray",length(XX[,1])),tmpcol)
plot3d(XXX,col=col)
#open3d()
lims<-range(Xsum)
plot3d(Xsum,col=tmpcol,xlim=lims,ylim=lims,zlim=lims)

# １つ目のシミュレーションの結果を保管
XsumOri<-Xsum
tmpcolOri<-tmpcol
Mori<-M

# ２つ目のシミュレーションを実施
M<-M2
Xsum<-NULL
tmpcol<-c()
currentM<-diag(n)
for(ir in 1:Nrep){
	#currentM<-currentM%*%M

	# 座標
	X<-matrix(0,Niter,n)

	# 初期座標
	X[1,]<-runif(n)
	X[1,]<-X[1,]/sqrt(sum(X[1,]^2))
	# シミュレーション
	for(i in 2:Niter){
		P<-X[i-1,]
		Q<-M%*%P
		PQ<-Q-P
		# PとQを通る平面をx1=x2平面に移す行列
		R<-XYRotation(P,PQ)
		tmpP<-R%*%P
		tmpQ<-S%*%tmpP
		newQ<-solve(R)%*%tmpQ
		
		currentdrift<-commondrift
		if(runif(1)<rarefreq)currentdrift<-raredrift
		X[i,]<-newQ+rnorm(n)*currentdrift
		X[i,]<-X[i,]/sqrt(sum(X[i,]^2))
	}
	Xsum<-rbind(Xsum,X[plotstart:length(X[,1]),])
	tmpcol<-c(tmpcol,rep(ir,(Niter-plotstart+1)))
}

normX<-sqrt(sum(Xsum[1,]^2))

NrandPt<-10000
XX<-matrix(rnorm(NrandPt*n),NrandPt,n)
XX<-XX/sqrt(apply(XX^2,1,sum))*normX

XXX<-rbind(XX,Xsum)
col<-c(rep("gray",length(XX[,1])),tmpcol)
plot3d(XXX,col=col)
#open3d()
lims<-range(Xsum)
plot3d(Xsum,col=tmpcol,xlim=lims,ylim=lims,zlim=lims)

# 第１、第２のシミュレーションの結果を併せて表示
X1sumX2sum<-rbind(XsumOri,Xsum)

XXX<-rbind(XX,X1sumX2sum)
col<-c(rep("gray",length(XX[,1])),rep(2,length(tmpcolOri)),rep(3,length(tmpcol)))
plot3d(XXX,col=col)

plot3d(X1sumX2sum,col=c(rep(2,length(tmpcolOri)),rep(3,length(tmpcol))),xlim=lims,ylim=lims,zlim=lims)

####繰り返して使用する関数
library(GPArotation)

# n次元空間で
# 原点を中心として、点Pが
# ベクトルVを接ベクトルとするような回転を表す行列

# デカルト座標を各座標に直す関数を使う
# デカルト座標から角座標へ
Cartesian2AngularX<-function(x){
	n<-length(x)
	if(n==1){
		return(list(r=abs(x),t=acos(sign(x))))
	}else if(n==2){
		tmpt<-0
		if(x[1]!=0){
			tmpt<-acos(x[1]/sqrt(sum(x^2)))*sign(x[2])
			if(sign(x[2])==0){
				if(x[1]>0){
					tmpt<-0
				}else if(x[1]<0){
					tmpt<-pi
				}
			}
			#tmpt<-atan(x[2]/x[1])
		}else{
			if(x[2]>0){
				tmpt<-pi/2
			}else if(x[2]<0){
				tmpt<--pi/2
			}
		}
		return(list(r=sqrt(sum(x^2)),t=tmpt))
	}
	r<-sqrt(sum(x^2))
	xst<-x/r
	#n<-length(xst)
	t<-rep(0,n-1)
	S<-C<-t
	S[n-1]<-xst[n]
	if(S[n-1]>1)S[n-1]<-1
	if(S[n-1]<(-1))S[n-1]<-(-1)
	t[n-1]<-asin(S[n-1])
	C[n-1]<-cos(t[n-1])
	cumC<-C[n-1]
	for(i in (n-2):1){
		if(cumC!=0){
			S[i]<-xst[i+1]/cumC
			if(S[i]>1)S[i]<-1
			if(S[i]<(-1))S[i]<-(-1)
			t[i]<-asin(S[i])
			C[i]<-cos(t[i])
			cumC<-cumC*C[i]
		}else{
			S[i]<-0
			t[i]<-asin(S[i])
			C[i]<-cos(t[i])
		}
		
	}
	list(r=r,t=t)
}

# (1,0,...,0)ベクトルを与えたベクトルに移す回転行列(もしくはその逆行列)を返す

VectorRotation<-function(P,inv=FALSE){ # inv=TRUEは逆行列
	n<-length(P)
	#print(n)
	if(n==1){
		return(matrix(c(1),1,1))
	}
	Q<-Cartesian2AngularX(P)

	M<-diag(n)
	M2<-M

	for(i in 1:length(Q[[2]])){
		tmp<-M
		tmp[i,i]<--sin(Q[[2]][i])
		tmp[i,i+1]<-cos(Q[[2]][i])
		tmp[i+1,i]<-cos(Q[[2]][i])
		tmp[i+1,i+1]<-sin(Q[[2]][i])
		M2<-tmp%*%M2
	}
	M2<-t(M2)[,n:1]
	
	S<-sign(M2[,1]*P)
	M2<-M2*S
	if(inv){
		M2<-solve(M2)
	}
	M2
}

# ２つのベクトルを取って
# その第１ベクトルを(1,0,...,0)に写し
# 第２ベクトルを(1,0,...,0)と(0,1,0,...,0)とが張る面に移す
# P,Vを第１・２軸平面に移す行列はinv=TRUE
# その逆はinv=FALSE
XYRotation<-function(P,V,inv=TRUE){
	# Pを(1,0,...,0)軸に回転する行列
	R1<-VectorRotation(P,inv=TRUE)
	# VそR1で回転して
	V2<-R1%*%V
	# その第１軸以外の成分を取り出して、この部分の回転を求める
	tmpV<-V2[2:length(V)]
	tmpR2<-VectorRotation(tmpV,inv=TRUE)
	R2<-diag(length(V))
	R2[2:n,2:n]<-tmpR2
	ret<-R2%*%R1
	if(!inv)ret<-solve(ret)
	ret
}