2012-03-28

複数観測点のデータを使う

lmer R

線形混合効果モデル(こちら)
パッケージの説明PDF
- メタアナリシスのときに、複数のスタディに等しいリスクを想定するのがFixed effectモデルで、異なるリスクを想定するのがrandom effectモデルですが、線形回帰のときに、ベースラインや、回帰直線の傾きについて、群ごとに同じで考えれば、Fixed、群ごとに違う値を考えればRandom。線形混合効果モデルでも、"Fixed effect","Random effect"がそういう文脈で使われています。
前置き：lmer()が挙動不審とのコメントあり。要注意(こちら)
ランダム・エフェクトを切片にのみでよければ、glmmML() in library(glmmML)でも
さて、４時刻にわたって、測定されたデータがあるものとする
- 横軸は時刻0,1,6,60が等間隔
- 縦軸は観測値
- 全体の傾向としては、明らかに右肩上がり
- ３色は、後述する３ジェノタイプで塗り分け
- 初期値が高めだけれど、傾きが小さいか、初期値が低めだけれど、傾きが大きいか、で３ジェノタイプには明らかな違いがある

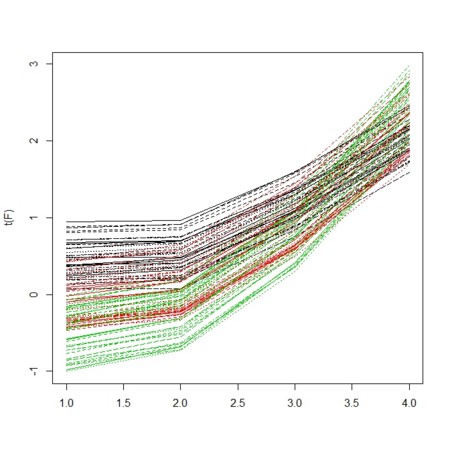
その４時刻には、１次線形なトレンドがあることが間違いないものとする
ここで、この１次線形なトレンドが、標本の属性(たとえば、2値型遺伝子多型のディプロタイプ)に関して(相加モデルで)影響されているかどうかを調べたいとする
標本の属性は、観測値のベースラインに影響する(経時的測定だが、その時刻によらず、常に同じ影響を与えている)かもしれない
標本の属性は、観測値のベースラインに影響を与えるとともに、経時的変化の傾きにも影響を与えているかもしれない
こんなことを調べたい
次のようにする
- ジェノタイプ・性別・年齢・サンプルIDを作る

library(lme4)
# サンプル数　Ns
Ns<-100
# 観測時刻数　Nt
nT<-4
# 観測時刻
T<-c(0,1,6,60)
# サンプルの属性情報
# サンプルID
I<-1:Ns
I<-paste("",I)
# ジェノタイプ
G<-sample(0:2,Ns,replace=TRUE)
# 年齢
A<-sample(30:80,Ns,replace=TRUE)
# 性別
B<-sample(0:1,Ns,replace=TRUE)

# サンプル属性を束ねる
S<-cbind(I,G,A,B)

- 観測データを作る

# 観測項目のデータ
# ジェノタイプと関連があるように作為的に作ってみる
# ジェノタイプの影響を受けるのは、初期値と、増加(傾き)の両方
F<-matrix(0,Ns,Nt)
F[,1]<-runif(Ns)-0.5*G
#F[,2]<-F[,1]+0.1*G*runif(Ns)
#F[,3]<-F[,2]+0.2*(G+3)*runif(Ns)
#F[,4]<-F[,3]+0.4*(G+2)*runif(Ns)
F[,2]<-F[,1]+0.1*G+runif(Ns)*0.1
F[,3]<-F[,2]+0.2*(G+3)+runif(Ns)*0.1
F[,4]<-F[,3]+0.4*(G+2)+runif(Ns)*0.1

matplot(t(F),type="l",col=(G+1))

# Fを長さNs*Ntのベクトルにする
Fv<-c(F)

- サンプル属性データの行数を観測項目のそれにそろえる
- 時刻も加える

# Fに合わせて、サンプル属性も行数Ns*Ntにする
Sv<-as.data.frame(S)
for(i in 2:Nt){
	Sv<-rbind(Sv,S)
}
# 観測時刻のベクトルを作る
T<-c(matrix(rep(t,Ns),byrow=TRUE,ncol=Nt))
Sv<-cbind(Sv,T)

- ３つのモデルを考える

# ３つのモデルを考える
# モデル１ 時間によって観察項目Fの値が1次線形に大きくなる。年齢、性別によるベースラインの影響はあるかもしれないが、年齢、性別による、増加率への影響はないものとするジェノタイプの影響はないものとする。個々のサンプルの個人差をベースラインに仮定する
# モデル２ ジェノタイプの影響で観察項目Fの値は時刻によらず、影響を受けるが、Fの増加率にはジェノタイプの影響が及ばないものとする。年齢、性別の影響はベースラインには考慮するが、増加率には考慮しないものとする。個々のサンプルの個人差をベースラインに仮定する
# モデル３　ジェノタイプの影響でFのベースラインが影響を受けるとともに、増加率も影響を受けるものとする。年齢、性別の影響はベースラインには考慮するが、増加率には考慮しないものとする。個々のサンプルの個人差をベースラインに仮定する

# モデル１
# (1|Sv$I)の項は、個人ひとりずつ、ベースラインの大きさに影響する項
m1out<-lmer(Fv~Sv$T+Sv$A+Sv$B+(1|Sv$I))
# モデル２
# (1|Sv$G)はジェノタイプが加算的にベースラインの大きさに影響する項
m2out<-lmer(Fv~Sv$T+Sv$A+Sv$B+(1|Sv$G)+(1|Sv$I))
# (Sv$T|Sv$G)はジェノタイプが加算的にベースラインと時間に関する傾きに影響を与える項
m3out<-lmer(Fv~Sv$T+Sv$A+Sv$B+(Sv$T|Sv$G)+(1|Sv$I))

- 回帰の結果を示す

m2out
fixef(m2out)
ranef(m2out)

- 回帰された値とオリジナルの値を比較する

# @y は入力値、@eta は回帰した値(らしい)
plot(m2out@y,m2out@eta)

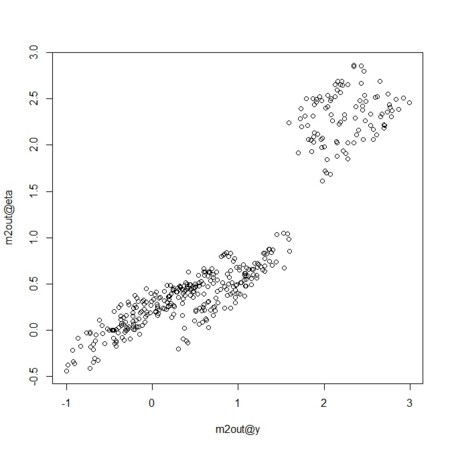
- 結果をanovaで検定する
  - 変数を増やしたモデルを増やす前のモデルに対して比較している

anova(m1out,m2out)
anova(m2out,m3out)

> anova(m1out,m2out)
Data: 
Models:
m1out: Fv ~ Sv$T + Sv$A + Sv$B + (1 | Sv$I)
m2out: Fv ~ Sv$T + Sv$A + Sv$B + (1 | Sv$G) + (1 | Sv$I)
      Df    AIC    BIC  logLik  Chisq Chi Df Pr(>Chisq)    
m1out 51 584.31 787.88 -241.16                             
m2out 52 569.42 776.98 -232.71 16.887      1  3.968e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
> anova(m2out,m3out)
Data: 
Models:
m2out: Fv ~ Sv$T + Sv$A + Sv$B + (1 | Sv$G) + (1 | Sv$I)
m3out: Fv ~ Sv$T + Sv$A + Sv$B + (Sv$T | Sv$G) + (1 | Sv$I)
      Df    AIC    BIC  logLik Chisq Chi Df Pr(>Chisq)    
m2out 52 569.42 776.98 -232.71                            
m3out 54 462.63 678.17 -177.31 110.8      2  < 2.2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

- 個人ごとの寄与を完全に個人をばらばらにしたが、GWAS-PCAの情報などを使って、主要軸を取りこんでもよい

# サンプルにeigenstratなどのPCAの軸情報が与えられた場合
# 軸数
Na<-3
# 適当に作る
P<-matrix(rnorm(Na*Ns),ncol=Na)
# 観測時点の数だけ増やした行列にする
Pv<-P
for(i in 2:Nt){
	Pv<-rbind(Pv,P)
}
# 上のやり方で取り込んだ個人差を、PCAの情報に置き換えてみる

m1out.P<-lmer(Fv~Sv$T+Sv$A+Sv$B+(1|Pv[,1])+(1|Pv[,2])+(1|Pv[,3]))
m2out.P<-lmer(Fv~Sv$T+Sv$A+Sv$B+(1|Sv$G)+(1|Pv[,1])+(1|Pv[,2])+(1|Pv[,3]))
m3out.P<-lmer(Fv~Sv$T+Sv$A+Sv$B+(Sv$T|Sv$G)+(1|Pv[,1])+(1|Pv[,2])+(1|Pv[,3]))
anova(m1out.P,m2out.P)
anova(m2out.P,m3out.P)

- すべてのサンプルに全時刻の情報がなくてもよい
  - サンプルごとに、時系列の切片と傾きを引く処理だから、観測時刻がばらばらでもよい

# 必ずしも、時刻データがそろっていなくてもよい
selected.time<-sample(1:length(Fv),length(Fv)/2)
Fv.s<-Fv[selected.time]
Sv.s<-Sv[selected.time,]
# 時刻はずれてもよい
Sv.s$T<-Sv.s$T*rnorm(length(selected.time),1,0.2)
plot(Sv$T[selected.time],Sv.s$T)

m1out.s<-lmer(Fv.s~Sv.s$T+Sv.s$A+Sv.s$B+(1|Sv.s$I))
m2out.s<-lmer(Fv.s~Sv.s$T+Sv.s$A+Sv.s$B+(1|Sv.s$G)+(1|Sv.s$I))
m3out.s<-lmer(Fv.s~Sv.s$T+Sv.s$A+Sv.s$B+(Sv.s$T|Sv.s$G)+(1|Sv.s$I))

anova(m1out.s,m2out.s)
anova(m2out.s,m3out.s)

# generalized mixed modelもありそうだが…そしてfamily引数を使うようだが…

glmer(Fv~Sv$T+Sv$A+Sv$B+(1|Sv$G)+(1|Pv[,1])+(1|Pv[,2])+(1|Pv[,3]),family=gaussian)