2013-05-16

なんちゃって正規直交基底

こちらで多次元オブジェクトの減次元視覚という話をしている
何かしらのルールで情報量の多さを定め、その多い順に軸を定めつつ、正規直交基底を取り出したい、ということ
PCAと同じ話
ただしPCAでは、情報量の多さとは、軸に関する分散の大きさであって、線形代数的に解けることになっている
今、情報量の多さについての定義を自由にしてしまったので(この先、正規直交基底の『直交』も必要条件でなくしていく予定(かもしれない)だったり、線形独立基底でもなく、適切な本数の軸、というくらい自由にするかもしれないのだけれど、ひとまず、正規直交基底は扱いやすいのでそうしておくとする)、線形代数で解くのはよろしくない
それよりは、視覚を発達させつつある乳幼児的に『矯めつ眇めつ』する方法を計算機にやらせたい
乳幼児は、情報量の多い軸をどうやって選んでいるのだろう？
大きく２つ考えられる
- １つ目の方法は、視点ごとに情報量の多寡を算出して、「最大値」を与える点を選びとる、という方法
- ２つ目の方法は、あれやこれや試しつつ、情報量が最大化する点に「山登り法」で到達する、と言う方法
どっちだろう？
- 前者は、たくさんの値から最大値を見つける作業があり、「たくさんの値」をストックする、という作業と、その中の最大値を見つけるという作業との２つがあって、簡単そうだけれど、「超原始的な計算機(である脳)しか持たない」ときには難しそう
- 後者は、探索する、網羅的に探索する、という作業が難しそうだが、そこに悉皆性を求めなければ２点の比較をするだけなので、情報のストックという意味でも、値の取り扱いという意味でも簡単そうだ
とはいえ、前者でやってみよう

install.packages("geometry")
library(geometry)

view.point.random <- function(d,n=10000){
	X <- matrix(rnorm(n*d),ncol=d)
	X/sqrt(apply(X^2,1,sum))
}
# あるベクトルを１つの軸とする正規直交基底
base.v <- function(v){
	d <- length(v)
	v <- v/sqrt(sum(v^2))
	ret <- matrix(0,d,d)
	for(i in 2:(d)){
		ret[1:(i-1),i] <- v[1:(i-1)]
		ret[i,i] <- -sum(v[1:(i-1)]^2)/v[i]
	}
	ret[,1] <- v
	q <- sqrt(apply(ret^2,2,sum))
	t(t(ret)/q)
}
var.v.p <- function(X,v.p){
	tmp <- X %*% v.p
	sum((tmp-mean(tmp))^2)
}

d <- 6

g <- 10
g.mean <- matrix(0,g,d)
library(MCMCpack)
g.mean[1:5,1:3] <- rdirichlet(1,rep(0.5,15)) * 100
g.mean[6:10,4:6] <- rdirichlet(1,rep(0.5,15)) * 100

g.n <- sample(50:100,g)

X <- matrix(0,nrow=0,ncol=d)
for(i in 1:g){
	tmp.X <- matrix(0,g.n[i],d)
	for(j in 1:d){
		tmp.X[,j] <- rnorm(g.n[i],g.mean[i,j])
	}
	X <- rbind(X,tmp.X)
}

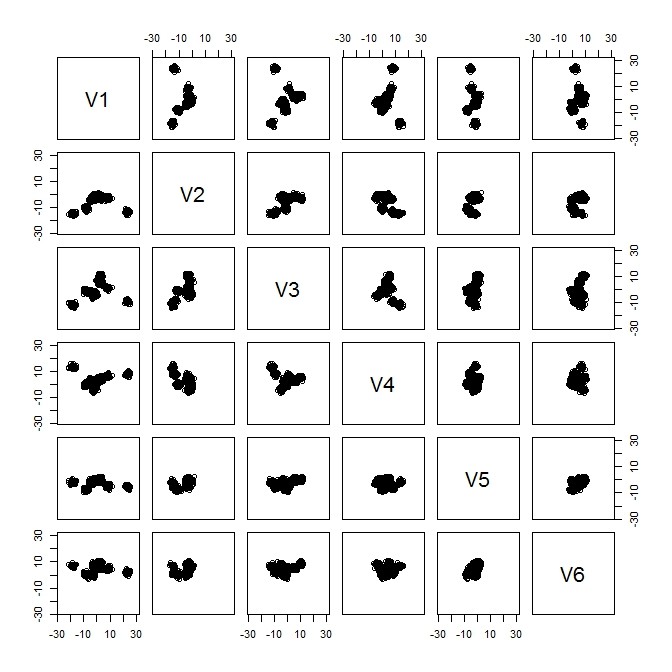
plot(as.data.frame(X))
my.v <- runif(d)
my.b <- base.v(my.v)
X.ori <- X
X <- t(my.b %*% t(X))
plot(as.data.frame(X),xlim=range(X),ylim=range(X))
m <- matrix(0,d,d)
b.list <- list()
for(i in 1:(d-1)){
	v.pts <- view.point.random(d+1-i)
	if(i == 1){
		tmp.val <- rep(0,length(v.pts[,1]))
		for(j in 1:length(tmp.val)){
			#tmp.val[j] <- area.v.p(X,v.pts[j,])
			tmp.val[j] <- var.v.p(X,v.pts[j,])
		}
		selected.v <- v.pts[which(tmp.val == max(tmp.val))[1],]
		b.list[[i]] <- base.v(selected.v)
	}else{
		tmp.m <- matrix(0,length(v.pts[,1]),i-1)
		v.pts.2 <- cbind(tmp.m,v.pts)
		v.pts.3 <- t(b.list[[i-1]] %*% t(v.pts.2))
		tmp.val <- rep(0,length(v.pts[,1]))
		for(j in 1:length(tmp.val)){
			#tmp.val[j] <- area.v.p(X,v.pts.3[j,])
			tmp.val[j] <- var.v.p(X,v.pts.3[j,])
		}
		selected.v.id <- which(tmp.val == max(tmp.val))[1]
		tmp.b <- base.v(v.pts[selected.v.id,])
		tmp.m <- matrix(0,length(tmp.b[,1]),i-1)
		tmp.b2 <- cbind(tmp.m,tmp.b)
		b.list[[i]] <- cbind(b.list[[i-1]][,1:(i-1)],(b.list[[i-1]]) %*% t(tmp.b2))
	}
}
X.2 <- t(t(b.list[[d-1]])%*% t(X))
#X.3 <- t((b.list[[d-1]])%*% t(X))

xlim <- ylim <- range(c(X,X.2,X.ori))
plot(as.data.frame(X),xlim=xlim,ylim=ylim)
dev.new()
plot(as.data.frame(X.2),xlim=xlim,ylim=ylim)
dev.new()
plot(as.data.frame(X.ori),xlim=xlim,ylim=ylim)

maxs <- rep(max(X),d)
mins <- rep(min(X),d)
X.add <- rbind(X,rbind(maxs,mins))

X.add.2 <- t(t(b.list[[d-1]])%*% t(X.add))
plot3d(X.add.2[,1:3])