 .Additive regression model
.Additive regression model- 1年間365日の気温観測値。スプライン、周期性を考慮してのフーリエ変換など、方法は複数あるが、結果は似たり寄ったり
- フィットの良さと平滑の良さとはどちらも2次形式。両者の塩梅をするとそれは線形最適化
- MMRのスパイクデータでは、orthogonal discrete wavelet transformがスムージングに成功している。閾値を使ってノイズのがたぼこをゼロにしている
- それに比べていわゆるカーネル推定やスプライン平滑化は、成功しない
- 大雑把に言うと、カーネル推定・スプライン平滑化では、「均す」ために考慮する幅をどこでも同じにするのに対して、wavelet transformationでは場所ごとによいと思われる幅にする点が違い、それが、de-noiseの仕方に影響を与えている
- wavelet transformationで少数のピークに集約されることが「分布・データの特長である!」とまとめようとしている…らしい
- 結晶と準結晶とがフーリエ変換で、櫛関数同士の関係だ、というのが、wavelet変換が観察の背後にあると考えているのは、次のようなことだ、ということに通じるようだ:"be concentrated in a relatively small number of wavelet coefficients, while the noise is scattered about globally and at an apprently constant standard deviation within and across levels"という表現
- 具体的な課題
- wavelet transfromationでの閾値はどのように(データ・ドリブンで)決めることができるか
- 線形な手法(カーネル推定・スプライン平滑化など)より有効なのはどういう場合なのか
- 数少ないぱらぱらしたスペクトルにまとめたいわけだが、「ぱらぱらして」いることはどういう役割を持つのか、どのように「ぱらぱらさ加減」を定量すればよいのか
- 「最適」な状態を表現できるのか
- 一般化するとして、どんな方向にどのように一般化できるのか
- Wiener filter
 で
で とは、
とは、 を分散とする正規分布に従う
を分散とする正規分布に従う があって、それに分散
があって、それに分散 の正規分布誤差を伴って観察するとき、観察値
の正規分布誤差を伴って観察するとき、観察値 から、その真値
から、その真値 を推定値
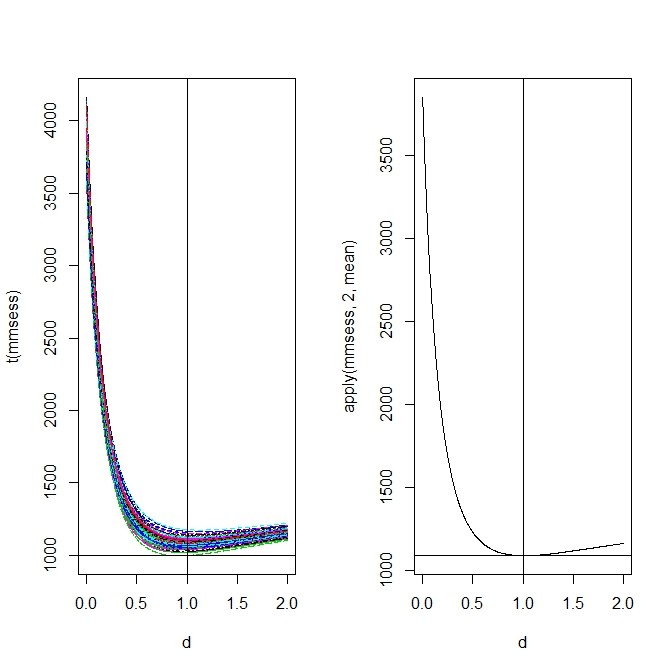
を推定値 で得ると、MMSE(minimum mean square error)が最小になるよ、という話
で得ると、MMSE(minimum mean square error)が最小になるよ、という話- Rでやってみる
n.iter <- 100
d <- seq(from=0,to=2,length=1000)
theta <- 0
tau <- runif(1)+1
theta. <- rnorm(n,theta,tau)
epsilon <- runif(1)+1
n <- 1000
mmsess <- matrix(0,n.iter,length(d))
for(ii in 1:n.iter){
y.obs <- theta.+ epsilon*rnorm(n)
rho <- (tau^2)/(epsilon^2)
theta.est <- rho/(rho+1)*y.obs
theta.est. <- matrix(0,length(d),n)
for(i in 1:length(theta.est)){
theta.est.[i,] <- rho/(rho+d[i])*y.obs
}
mmse <- sum((theta.est-theta.)^2)
mmses <- rep(0,length(d))
for(i in 1:length(d)){
mmses[i] <- sum((theta.est.[i,]-theta.)^2)
mmsess[ii,i] <- sum((theta.est.[i,]-theta.)^2)
}
plot(d,mmses,type="l")
abline(v=1)
abline(h=mmse)
}
par(mfcol=c(1,2))
matplot(d,t(mmsess),type="l")
abline(v=1)
abline(h=min(mmsess))
plot(d,apply(mmsess,2,mean),type="l")
abline(v=1)
abline(h=min(apply(mmsess,2,mean)))
par(mfcol=c(1,1))
 ノルムでSparcityを評価。軸の取り方の違いで、軸に集中して値づけがなされているかの評価ができる
ノルムでSparcityを評価。軸の取り方の違いで、軸に集中して値づけがなされているかの評価ができる
- うまく適合するように閾値を入れるという方法で小さいpでの
 ノルムが小さくなるようにする、という作戦は、放っておけば、いくらでもフィットの良いものができる
ノルムが小さくなるようにする、という作戦は、放っておけば、いくらでもフィットの良いものができる
- そこでそれを制約するために、「最適なフィット」を探す側と、その裏をかく側との対決とし、相互の「よさ」の関数の妥協点を探す、という問題にしてみよう、というのがminimax戦略
- このminimax戦略は
 のどちらを基準にするかで、見え方が違う
のどちらを基準にするかで、見え方が違う
- 通常の方法
 の方では、minimax estimatorが線形、裏をかく側を評価するのは正規分布、minimaxMSEは1/2
の方では、minimax estimatorが線形、裏をかく側を評価するのは正規分布、minimaxMSEは1/2
- Spariciyを用いる方法では、minimax estimatorは閾値決定、裏をかく側を評価するのは、Sparcity、minimaxMSEは

- 離散的時刻観察
- 等時刻間隔での観察をn回するということは、真値として長さnのベクトル(ただし、これは離散時刻を引数にしたある関数の値とみなす)が、観察値として長さnのベクトルが、誤差項に対応する長さnのベクトルが、それぞれ得られる
- 正規直交基底で誤差項が小さくなるようにして、スムージングも達成するようにする、という処理がスプライン平滑化であって、誤差と平滑の2変数の折り合いをつける最適化、という問題で解いてもよいし、最適な直交基底探しをしてsparcityの最小化を探索してもよい。どちらも同じだ、ということは、どちらも探索空間とその上での最適解との置かれ方(探索の容易さ)はある意味で同じであることも示せる
- Continuous Gaussian white noise model
- 時刻に関して連続観察してしまうのがこのモデル。真の時刻変化が関数で与えられているのは、上記の離散時刻モデルと同じ。誤差項が連続時間の積分になる
- 誤差の連続時間積文は連続時間のブラウン運動・ウィーナー過程
.Additive regression model
ノルムでSparcityを評価。軸の取り方の違いで、軸に集中して値づけがなされているかの評価ができる
ノルムが小さくなるようにする、という作戦は、放っておけば、いくらでもフィットの良いものができる
のどちらを基準にするかで、見え方が違う
