- 場所によってたくさん読まれるところと少なく読まれるところがある
- 興味は大きく分けて二つ
- 読まれた部位に違い(多型とか)があるかもしれないときに、多型があるか、あるならアレルは何か、その割合の推定値はいくつか(ホモとヘテロだけであれば、ホモか、ヘテロ化、プールサンプルなら、アレルの比率。アレル特異的トランスクリプトの比率もこれと同様)
- 読まれた部位を相互に比較して、その相対量を数値化
- いずれにしても、部位によってリード数が多くなりやすさが違うこと、同じ部位の異なる配列のリード数は観測量であって、本当に知りたいのはサンプルの量(比)だから、推定する必要がある。Deep sequencing/Massive pararell sequencingでは、この部位によるばらつき、配列の違いによる読まれやすさの多寡を制御できないので、出たデータからその制御できていないことを織り込んで答えを(幅付きで)推定する作業が発生する
- この章はそういう話
- 平均して1塩基対(ヒトのゲノムは30億塩基対)あたり何回読まれたか
- 各塩基対は何回読まれるか
- ポアッソン分布とみなす
- ポアッソン分布は、すべての位置が実験的に平等であるとの前提のモデルであって、実際はそうではないので、あくまでも、「単純化したモデル」。
- ゲノムのどこが読まれるかはランダムに決まるとして、平均して
 回、読まれているとすると、
回、読まれているとすると、 回読まれる箇所の比率はどうなっているか、と言う分布
回読まれる箇所の比率はどうなっているか、と言う分布
- ある部分(長さLのエクソン上)に、長さKのリードが何本乗るかという計算だと
 を平均としたポアソン分布とみなせる
を平均としたポアソン分布とみなせる
 は1塩基対当たりの平均リード数
は1塩基対当たりの平均リード数- そのリードの始点と領域の始点との位置関係は
 のときに領域とリードはかぶっているから
のときに領域とリードはかぶっているから 倍してある
倍してある
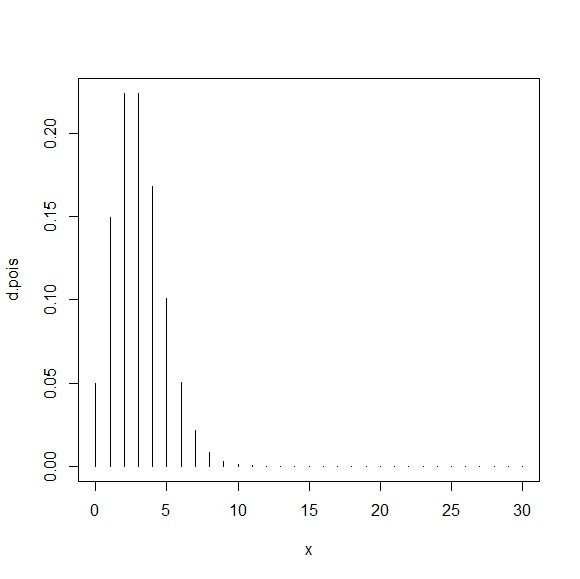
beta <- 3
x <- 0:30
d.pois <- dpois(x,beta)
plot(x,d.pois,type="h")
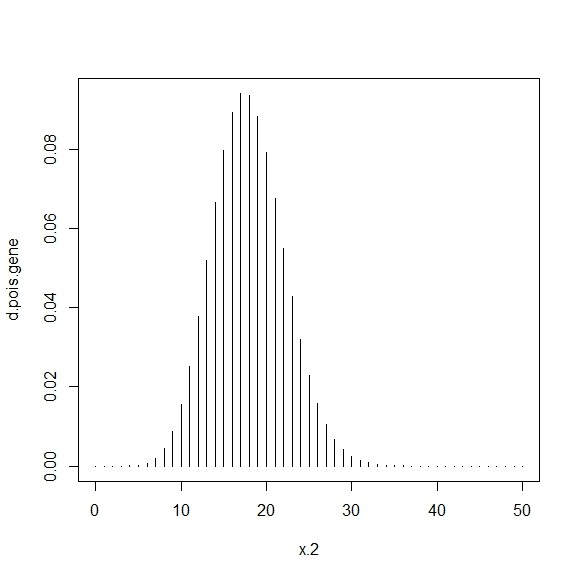
L <- 200
K <- 40
x.2 <- 0:50
d.pois.gene <- dpois(x.2,beta/K*(L+K-1))
plot(x.2,d.pois.gene,type="h")
 をゲノムの位置の関数にするモデル
をゲノムの位置の関数にするモデル
- ゲノム全体で
 を一様としたのが上のモデル
を一様としたのが上のモデル
 をGC比率の関数にすることもできる
をGC比率の関数にすることもできる
- (たとえば)位置xのGC比率が
 とすれば
とすれば
 のようにおくことができる。
のようにおくことができる。 が観察データとうまく合うように推定(最尤推定)することもできる
が観察データとうまく合うように推定(最尤推定)することもできる- また、
 という帰無仮説(ゲノム全体で同じ
という帰無仮説(ゲノム全体で同じ )と
)と という対立仮説のどちらを採用するのがよいか、後者を採用するなら、いくつの値を採用するのがよいか、ということも、通常の統計処理の範囲になる
という対立仮説のどちらを採用するのがよいか、後者を採用するなら、いくつの値を採用するのがよいか、ということも、通常の統計処理の範囲になる
- 逆に言うとある位置を読んだリード数から、その位置由来のテンプレート(たとえばトランスクリプトの量)を推定するときには、この
 の設定をどうするかによって、多いのか少ないのかの結果は変わってくる、ということ
の設定をどうするかによって、多いのか少ないのかの結果は変わってくる、ということ
- 分散に現れる、部位別の
 のばらつき
のばらつき
- ゲノム全体に同じ
 を使う、GC比率を考慮した
を使う、GC比率を考慮した 、その他の要素も加味した
、その他の要素も加味した 、と色々作れる
、と色々作れる
- とてもうまい
 の関数が作れれば、観測データがきれいにポアッソン分布に乗ってくるが、実際には、乗らない。(ポアッソン分布であるという仮定が正しいとしても)考慮していない因子があるからである。
の関数が作れれば、観測データがきれいにポアッソン分布に乗ってくるが、実際には、乗らない。(ポアッソン分布であるという仮定が正しいとしても)考慮していない因子があるからである。
- ポアッソン分布は
 を与えると平均と分散の両方が決まるが、今、平均がうまく合うように
を与えると平均と分散の両方が決まるが、今、平均がうまく合うように を調整しているので、うまく合わない部分は観測データの分散とポアッソン分布からの理論的分散との違いとして生じる。それを用いて、どれくらい、モデルがあっていないかの評価をすることはできる
を調整しているので、うまく合わない部分は観測データの分散とポアッソン分布からの理論的分散との違いとして生じる。それを用いて、どれくらい、モデルがあっていないかの評価をすることはできる
- 実験の増幅過程によるバイアス
- サンプルにPCRをかける過程が入ると、たまたま増幅されることになるか、たまたまもれるか、の影響が増幅する。その影響も大きい
- Overdispersion
- この偶然の要素を伴ってばらつくのは"overdispersion"と呼ばれる
- 本来こうあるべきところがわからないけれど、それより多くなったり少なくなったりする、という枠組みで観察データが得られているときに、元のあるべきところの値を分布として推定するのは、「事前分布→観察→事後分布」という推定技術の仕事
- では、この部位ごとの
 を変えつつ、分散がポアソン分布よりも大き目になっている、という状況をどう扱おうか、確率分布で扱えることがよい、なぜなら、パラメタで表された分布の問題に落とせば、パラメタ推定するだけで済むから
を変えつつ、分散がポアソン分布よりも大き目になっている、という状況をどう扱おうか、確率分布で扱えることがよい、なぜなら、パラメタで表された分布の問題に落とせば、パラメタ推定するだけで済むから
- 2つの段階
- 部位xでの
 をxに観測される値
をxに観測される値 の関数
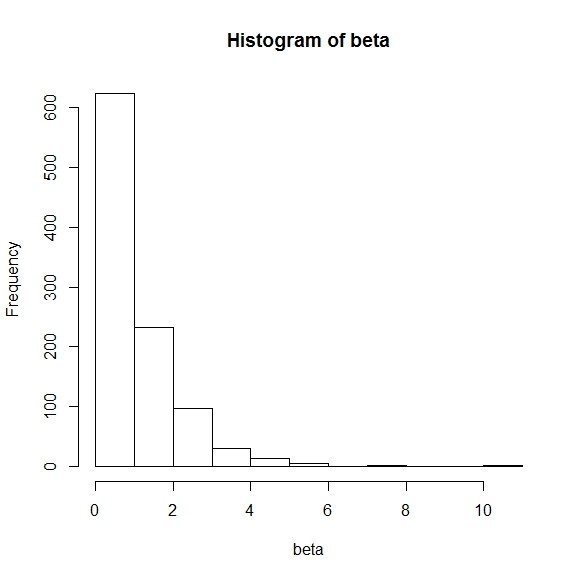
の関数 とすることにする。ガンマ分布がまずまずのようだ。なぜなら、0以上の値を取って、結構小さい値にたまっている形を作れるから
とすることにする。ガンマ分布がまずまずのようだ。なぜなら、0以上の値を取って、結構小さい値にたまっている形を作れるから
n <- 1000
sp <- 1
beta <- rgamma(n,sp)
hist(beta)
- 負の二項分布に近似する
- 次に、ポアソン分布らしさがあるが、それよりも分散が大き目overdispersionする分布をとる
- 負の二項分布がその条件を満足する
- ポアソン分布は「単位時間・単位範囲内の平均発生回数がm回であるときに、
 回となる場合の相対頻度」を表す
回となる場合の相対頻度」を表す
- 負の二項分布は、「ある回数の失敗が起きるまでに
 回成功するかの確率」を表す。ポアソン分布と違うのは、「打ち止め」があること。逆に言うと、無限回の失敗を許したうえで、これを行い、一定時間内・一定単位範囲内で起きる成功回数の平均値がある値になるように、時間幅・範囲幅を設定すれば、これはポアソン分布そのものとなる
回成功するかの確率」を表す。ポアソン分布と違うのは、「打ち止め」があること。逆に言うと、無限回の失敗を許したうえで、これを行い、一定時間内・一定単位範囲内で起きる成功回数の平均値がある値になるように、時間幅・範囲幅を設定すれば、これはポアソン分布そのものとなる
- このような負の二項分布は、生起確率p、許容する失敗回数rのときに成功回数がkである確率として
 で表される
で表される
- これの平均は
 、分散は
、分散は となり、確かに
となり、確かに のとき、平均も分散も
のとき、平均も分散も になって、ポアソン分布で平均と分散とが同じであることに符合する
になって、ポアソン分布で平均と分散とが同じであることに符合する
- Rでいじっておく
my.dnegbinom <- function(x,k,r){
choose(k+r-1,k)*(1-x)^r*x^k
}
my.rnegbinom <- function(n,p,r,s=20){
m <- p*r/(1-p)
sd <- sqrt(p*r)/(1-p)
k <- seq(from=0,to=m+s*sd,by=1)
tmp <- my.dnegbinom(p,k,r)
tmp.s <- sample(k,n,replace=TRUE,prob=tmp/sum(tmp))
}
p <- 0.3
r <- 4
n <- 10000
s <- 100
out <- my.rnegbinom(n,p,r,s)
mean(out)
p*r/(1-p)
var(out)
p*r/((1-p)^2)
m <- p*r/(1-p)
m+m^2/r
plot(0:max(out),tabulate(out+1),type="h")
- ポアソン分布・負の二項分布に照らして、データを読み取る
- どんな問題に使うか
- 多型箇所のジェノタイプコール・アレル頻度推定
- CNV検出
- 検出量にサンプル間で違いがあるかどうかの検定
- どう、使うか
- 各座位でどの塩基が何本分か、という情報が得られている
- そこの真実のアレルの具合(1人のサンプルなら、アレルMとアレルmとが0.5:0.5、プールサンプルなら、KホントL本、トランスクリプトならu:v)のときに全部で何リード観測したときに、どのアレルが何リード分になるか、が分布で出る
- この観察データに基づいて、元のサンプルの状態の最尤推定を行うことは(ポアソン分布モデル・負の二項分布モデルに照らして)可能
- 実際
- 異なる2タイプの比の推定
- ある座位がワイルドタイプがu本とミュータントタイプがv本だとする
- 「その座位」で「ワイルドタイプだったら」、平均
 とかの「リード数を推定するための変数」が得られる。ポアソン分布ならこれだけでよいし、負の二項分布なら、もう一つ変数がいる
とかの「リード数を推定するための変数」が得られる。ポアソン分布ならこれだけでよいし、負の二項分布なら、もう一つ変数がいる
- どうように「その座位」で「ミュータントタイプだったら」…という変数が得られる
- その上で、「ワイルドタイプ」のリード数が何本になるかの確率分布が計算できる。ミュータントタイプのそれも計算できる
- その値は仮定したu,vの値の取り方で変わる
- 今、ワイルドタイプとミュータントタイプの観測本数はわかっているので、u,vの値がどんな値のときに、そのような観測結果が得られやすいかが計算できる
- u,vの比率の推定なら、そうすればよい
- ジェノタイプコールなら、ホモ・ヘテロ・逆ホモのそれぞれの尤度が出て、明らかにどれかのジェノタイプとみなすのが良ければ、そうコールすればよいし、判断しにくければ、その判断しにくさを数値として示せばよい
- 帰無仮説検定
- 帰無仮説検定をするなら、上の流れの中でu=vという帰無仮説と、
 という対立仮説とで尤度比検定してもよい
という対立仮説とで尤度比検定してもよい
- レアバリアントか、ただのゴミかを見たいなら、非ワイルドタイプアレルが実験エラーとして観察される確率を定めると、「帰無仮説〜ワイルドタイプである」の下では、非ワイルドタイプのリードが読まれるのはこのエラー率そのものだから、このエラー率と、エラー率より多めに読まれるぶれを正規分布に照らして範囲をとり、それより多い非ワイルドタイプリード数なら、「ワイルドタイプである」という帰無仮説が棄却され、1か2本の非ワイルドタイプがあるという対立仮説を採用したい、ということになる。正規分布に照らした範囲の取り方でカットオフが決まってくる
- コピー数が普通じゃないことの検出
 なり、期待されるリード数と比較して、アカラサマに多すぎる・少なすぎる本数というものが観察されたら、それは、そもそも、「2コピー」からのリードだと仮定したのが間違いだったのでは…という形でコピーナンバーバリアントであるとみなすこともできる
なり、期待されるリード数と比較して、アカラサマに多すぎる・少なすぎる本数というものが観察されたら、それは、そもそも、「2コピー」からのリードだと仮定したのが間違いだったのでは…という形でコピーナンバーバリアントであるとみなすこともできる- 塩基単位での
 でやらずに、セグメント単位での
でやらずに、セグメント単位での でやれば、セグメントでの評価になる。こちらの方が、一連のコピーナンバー情報を総括しているので、原則的に有力になる
でやれば、セグメントでの評価になる。こちらの方が、一連のコピーナンバー情報を総括しているので、原則的に有力になる
- どこからどこまでがCNVか決まっていない状況でこれをやろうと思えば、ウィンドウを振らないといけなくて、それはCNV箇所推定問題と同様の課題を孕む
をゲノムの位置の関数にするモデル
の設定をどうするかによって、多いのか少ないのかの結果は変わってくる、ということ
のばらつき
を使う、GC比率を考慮した
、その他の要素も加味した
、と色々作れる
の関数が作れれば、観測データがきれいにポアッソン分布に乗ってくるが、実際には、乗らない。(ポアッソン分布であるという仮定が正しいとしても)考慮していない因子があるからである。
を与えると平均と分散の両方が決まるが、今、平均がうまく合うように
を調整しているので、うまく合わない部分は観測データの分散とポアッソン分布からの理論的分散との違いとして生じる。それを用いて、どれくらい、モデルがあっていないかの評価をすることはできる
を変えつつ、分散がポアソン分布よりも大き目になっている、という状況をどう扱おうか、確率分布で扱えることがよい、なぜなら、パラメタで表された分布の問題に落とせば、パラメタ推定するだけで済むから
をxに観測される値
の関数
とすることにする。ガンマ分布がまずまずのようだ。なぜなら、0以上の値を取って、結構小さい値にたまっている形を作れるから
回となる場合の相対頻度」を表す
回成功するかの確率」を表す。ポアソン分布と違うのは、「打ち止め」があること。逆に言うと、無限回の失敗を許したうえで、これを行い、一定時間内・一定単位範囲内で起きる成功回数の平均値がある値になるように、時間幅・範囲幅を設定すれば、これはポアソン分布そのものとなる
で表される
、分散は
となり、確かに
のとき、平均も分散も
になって、ポアソン分布で平均と分散とが同じであることに符合する
とかの「リード数を推定するための変数」が得られる。ポアソン分布ならこれだけでよいし、負の二項分布なら、もう一つ変数がいる
という対立仮説とで尤度比検定してもよい


