カーネル分布推定をBUGSで - ryamadaの遺伝学・遺伝統計学メモ

昨日は混合比の推定も含めた、混合分布推定をBUGSでやった(こちら)
ある一次元データが得られたとき、その個々の観測を中心としたカーネル関数の混合分布として背景の分布を推定することがある
カーネル関数として正規分布を取ることも多く、そのときに問題となるのは、正規分布の分散をいくつにしたらよいかを調整する必要があるということ
これをBUGSでやってみよう
まずはモデル
- 観測値がyというベクトルで観測数がN
- そのyのそれぞれの値を中心とし、共通のtauによって定められる正規分布(N個の正規分布)から、値を採取する(この中心の値にはmmという変数を使って書いてある。yと同じベクトル)
- N個の分布のどれにするかは、等確率で取る(dcat(piで指定。ただし、このpiに、等確率ベクトルを与える)。それによって決まったg[i]に対応するmmの値を中心とした正規分布からyを採取する
- tauには無情報を仮定して、分散の大きなガンマ分布からの値を取る

model6 <- function()
{
    for (i in 1:N) {
        y[i] ~ dnorm(m[i], tau)
        m[i] <- mm[g[i]]
        g[i] ~ dcat(pi[])
    }

    tau ~ dgamma(0.0001,0.0001)
}
file.name <- "model6.txt"
write.model(model6,file.name)

データを作って

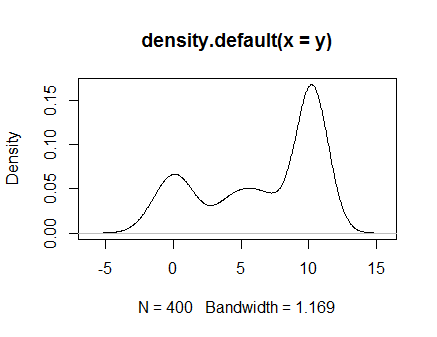
y <- c(rnorm(100),runif(100,3,8),rexp(200,4)+10)
y <- sort(y)
plot(density(y))

さて、BUGS実行

# 要素数
N <- length(y)
# mmとしてyと同じベクトルを与える
# 混合分布だが、N個の混合分布。g=1:NとしてN個のグループを与える。どのみちどのグループからとられるかは等確率でサンプリングするので、決め打ちにしてかまわない
# pi によってN個のうちのどの分布から採取するかを等確率で決める
data1 <- list(y=y,mm=y,N=N,g=1:N,pi=rep(1/N,N)) 
in1 <- list(tau=1) 
inits <- list(in1) 
param <- c("tau") 
file.name <- "model6.txt"
model1 <- file.name
# 実行
bugs6 <- bugs(data1, inits, param, model.file=model1, 
n.chains=1, n.iter=1100, n.burnin=100, n.thin=1, debug=TRUE, program="OpenBUGS", bugs.directory="C:/Program Files(x86)/OpenBUGS/OpenBUGS323")
print(bugs6)

結果

> print(bugs6)
Inference for Bugs model at "model6.txt", fit using OpenBUGS,
 1 chains, each with 1100 iterations (first 100 discarded)
 n.sims = 1000 iterations saved
              mean       sd      2.5%       25%       50%       75%
tau      2000861.2 139442.3 1737639.4 1902228.9 2000254.2 2094249.0
deviance    -274.3     28.0    -325.8    -293.6    -275.2    -255.1
             97.5%
tau      2270276.1
deviance    -218.9

DIC info (using the rule, pD = Dbar-Dhat)
pD = 1.0 and DIC = -273.4
DIC is an estimate of expected predictive error (lower deviance is better).

いわゆるdensity()の出力と比較してみる

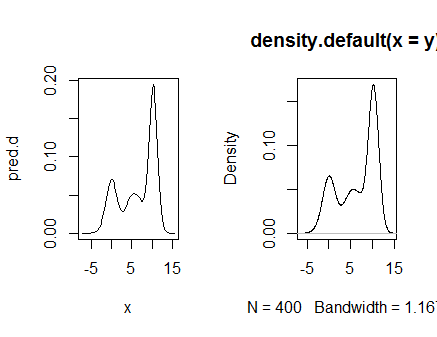
post6 <- bugs6$sims.matrix
out6.coef <- apply(post6,2,mean)
x <- seq(from=min(y)-(max(y)-min(y))*0.3,to=max(y)+(max(y)-min(y))*0.3,length=100)
pred.d <- rep(0,length(x))
for(i in 1:length(y)){
  pred.d <- pred.d + dnorm(x-y[i],1/sqrt(out6.coef[1]))/length(y)
}
par(mfcol=c(1,2))
plot(x,pred.d,type="l")
plot(density(y))
par(mfcol=c(1,1))