ARIMAと三角関数

• こちらで三角関数の級数表現について書いた
• 三角関数は、ある値が１個与えられたときに、それを無限に再帰的に使いまわす時系列データであるとわかった
• では「ある値が１個」与えられただけではなくて、そこに毎回、乱雑項が入るようにすれば、三角関数的ARIMAになる
• それを、「再帰なし」の場合と、「乱雑項なし」の場合と比較してみる

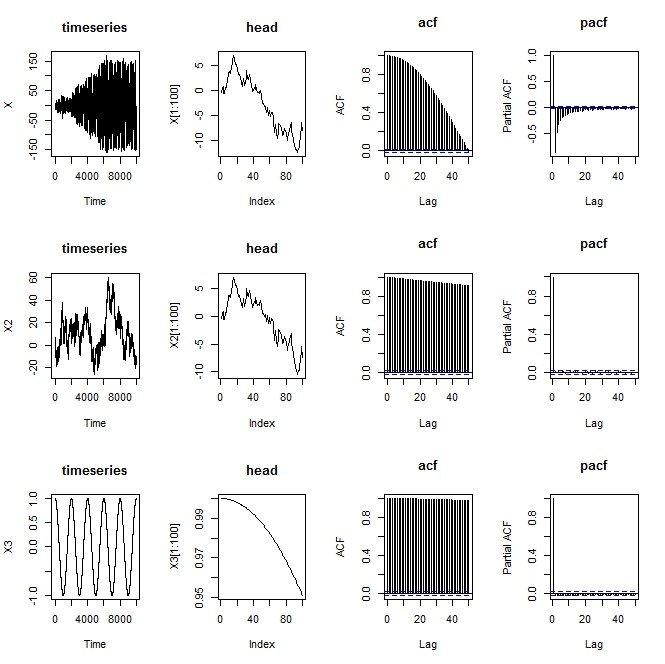
• Pが小さいときは「再帰なし」と「乱雑項なしの三角関数」はともに、pacfの結果から、第1要素の寄与のみであることがわかる

P <- 0.001
N <- 10^4
n <- N
z <- rnorm(N)
ar <- c(1-P,rep(-P,n))
ar2 <- 1-P
# 無限再帰(のつもり)：乱雑項アリの三角関数様
X <- filter(z,ar,method="r")
# 再帰なし
X2 <- filter(z,ar2,method="r")
# 理論的三角関数
X3 <- ts(cos((1:N)*P*pi),start=1,end=N)

lag.max <- 50
par(mfrow=c(3,4))
plot(X,type="l",main="timeseries")
plot(X[1:100],type="l",main="head")
acf(X,lag.max=lag.max,main="acf")
pacf(X,lag.max=lag.max,main="pacf")
plot(X2,type="l",main="timeseries")
plot(X2[1:100],type="l",main="head")
acf(X2,lag.max=lag.max,main="acf")
pacf(X2,lag.max=lag.max,main="pacf")
plot(X3,type="l",main="timeseries")
plot(X3[1:100],type="l",main="head")
acf(X3,lag.max=lag.max,main="acf")
pacf(X3,lag.max=lag.max,main="pacf")
par(mfcol=c(1,1))

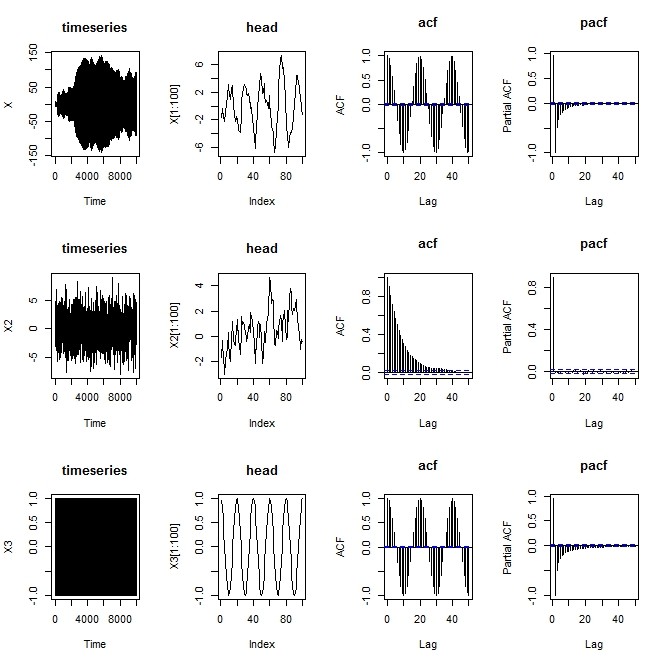
• Pが大きくなると、乱雑項なし・あり両方の三角関数でacfに周期性が登場し(autocorrelationが無限に続く)、pacfにも、第二項以降、負の寄与分が減衰しながら認められる

P <- 0.1
N <- 10^4
n <- N
z <- rnorm(N)
ar <- c(1-P,rep(-P,n))
ar2 <- 1-P
# 無限再帰(のつもり)：乱雑項アリの三角関数様
X <- filter(z,ar,method="r")
# 再帰なし
X2 <- filter(z,ar2,method="r")
# 理論的三角関数
X3 <- ts(cos((1:N)*P*pi),start=1,end=N)

lag.max <- 50
par(mfrow=c(3,4))
plot(X,type="l",main="timeseries")
plot(X[1:100],type="l",main="head")
acf(X,lag.max=lag.max,main="acf")
pacf(X,lag.max=lag.max,main="pacf")
plot(X2,type="l",main="timeseries")
plot(X2[1:100],type="l",main="head")
acf(X2,lag.max=lag.max,main="acf")
pacf(X2,lag.max=lag.max,main="pacf")
plot(X3,type="l",main="timeseries")
plot(X3[1:100],type="l",main="head")
acf(X3,lag.max=lag.max,main="acf")
pacf(X3,lag.max=lag.max,main="pacf")
par(mfcol=c(1,1))