ランダム行列の基礎

• このPDFに沿って、ランダム行列の基礎を学ぶ。
• こちらのサイトにあるように"One of the main questions on this subject is: given a matrix M whose entries are taken randomly from a known distribution, what would the distribution for its eigenvalues be?"
• Rを使う

ぱらぱらめくる『ディープラーニングと物理学』

ディープラーニングと物理学　原理がわかる、応用ができる （KS物理専門書） [ 田中 章詞 ]

第１章　はじめに：機械学習と物理学

第１部　物理から見るディープラーニングの原理

• 情報量は驚きの大きさ
• 生起確率P(A)に対して、を情報量とする
• 確率変数には、の情報量が期待される(情報量の期待値、平均情報量)
• 生起確率がn等分の場合、平均情報量は
• 物理の系のエントロピーはこの値
• 物理学における情報量上の課題など。ブラックホールでは情報が失われる。パラドクス的な話は情報が出入りしていないかに着目して解消することもある
• 最尤推定は、KLd的に、を最小にするようなを推定すること。KLdを(物理学では)相対エントロピーと呼ぶ
• 物理と(KLdを使う)学習とは、情報でつながっているから、物理と学習もつながるのでは？
• パターン形成が起きたとすると、それは情報を使っていたと考えるべき(自発的にパターンが生じる現象は、(多分)別の話)
• 学習において、微分は残差、積分は特徴量。物理において、運動方程式で速さが微分、位置が積分。

第２章　機械学習の一般論

• オッカムの剃刀は物理でいうところの、「単純なモデルの追求」に相当
• 深層学習のoverfitting回避性能のうまい説明はまだない
• 深層学習では、データをランダムに分割することでoverfittingを避ける一助にしている
• 情報幾何的な空間に反ド・シッター時空というものがあり、超弦理論で登場するという。

第３章　ニューラルネットワークの基礎

• 粒子が独立ではなく関係しあっていることは、２つの粒子の座標との距離に依存した項がハミルトニアンに加わるということで、結局という項の係数が0ではないことを意味する
• 学習では、何かと何かが関係しているかどうかを検出することが基本作業である。ハミルトニアンを立て、説明変数と被説明変数との積に関する項が０でない係数を持つかどうかを考える問題になる
• 熱力学では、実現されうるすべての場合と、特定の場合との比が、生起確率となると考え、そのような分布がボルツマン分布
• そのような設定から、誤差関数が導出できて、学習においては、その誤差関数の最小化をアルゴリズム的に実行している
• この時に出てくる誤差関数が、シグモイド関数や、その拡張であるsoftmax関数となっている
• ニューラルネットワークの各層では、非線形関数が適用され、出力として、統計力学的な意味での期待値が算出される
• 逆誤差伝搬法は、誤差関数の値を小さくするための方向を算出するもの。ブラとケットが順方向・逆方向に対応する
• ニューラルネットワークの万能近似定理。目的関数の非線形近似が得られ、中間層の数が増えれば増えるほど近似がよくなる
• 層の追加の効果は指数関数的な近似の改善をもたらす

第４章　発展的なニューラルネットワーク

• 畳み込みは座標非依存にする
• 学習結果を出力するときにも、畳み込みの逆を行うことがある。転置畳み込み
• 時系列情報処理には、前後時刻情報を入れる再帰的ネットワーク
• 勾配爆発・勾配消失があるとネットワークがうまく機能しない。更新過程を記憶しておく仕組み、解消する仕組みの導入により回避されうる(これは量子もつれ、とか、確定による情報消失等に対応する？)
• 注意機構という外部機構を入れることで性能が大幅に改善する場合もある(これは物理学で何に相当する？)
• ソートアルゴリズムとソリトン波は同じこと
• １次元セルオートマトンでチューリング完全な世界が構成できる、言い換えるとコンピュータを持ちうる世界を構成できる。このことは、現代社会がコンピュータを所有している物理的世界の仕組みについて何か意味を持つのか、否か？？

第５章　サンプリングの必要性と原理

• 物理との関係が今一つはっきりしないが…
• 量子ランダムウォークとかとマルコフ連鎖による、定常状態からのサンプリングの実現などが結びつくということだろうか
• 次章で用いるサンプリングへの導入的な意味が強い章か？

第６章　教師なし深層学習

• 教師データがないので、サンプリングを用いて最小化対象を計算可能にする
• 相反する目的を持った学習同士を競わせる(GAN: Generative Adversarial Network)
• 問題を双対に変換するのは学習でも物理でも同じ

第２部　物理学への応用と展開

第７章　物理学における逆問題

• 直接的に測ることができない対象を知ること、結果から原因を推定すること、物理法則・支配方程式の決定、物理定数の決定など
• ニューラルネットワーク構造になっている脳を持った人間が、自然を観測し、物理法則を見出したのだから、それよりある意味で高性能な深層学習はさらに物理法則を見出すのでは？
• (では、そこでの数学の役割とは、何だろう？ある設定の下での規則を見出すことが数学ならば、同様に深層学習が生み出す定理とか、予想とかがあるのでは。さらに、『新しい数学』という「うまくできている人工的な仕組み～ニューラルネットワークが説明可能な仕組み～』の創出も？)
• 大事なのは「情報」が必要だということ。物理での情報は「観察」。量子力学では、「観察」することは「系に介入」することになっている

第８章　相転移をディープラーニングで見いだせるか

第９章　力学系とニューラルネットワーク

第10章　スピングラスとニューラルネットワーク

第11章　量子多体系、テンソルネットワークとニューラルネットワーク

第12章　超弦理論への応用

第13章　おわりに

個人に複数の観察

lmer とか GEEとかもあるけれど、単純に回帰してもよい？

ぱらぱらめくる『量子ウォーク』

量子ウォーク [ 今野紀雄 ]

• 量子は複数の状態を持ちうる
• 例えば２状態なら上向きスピンと下向きスピンとか
• 複数の状態を持つ量子がランダムウォークするとき、どっちにどのくらいの確率で移動するかと、移動した後、状態が変わるか変わらないか、変わるなら何に変わるかのルールを入れる必要がある
• 量子ウォークはその話
• この本では、簡単な場合（１次元空間、かつ、離散空間）を中心に話を進める
• どっちに移動、と、状態変化をどうするかとの関係性から、それを表す行列表現が変わってくる
• その設定の中に、扱いやすいものがあったり、実際に物理学的に存在する対象があったり、なかったりするようだ
• ここで使う行列はユニタリー行列を使う事になるらしい。それは、状態に作用させた後、やっぱり、状態が「確率の条件〜全部で１」を満足するようになるため
• グラフ上での量子ウォークのためにグローバー行列というのがあって、辺接続情報の行列だが、この場合、ある辺がある頂点に入って行き、その後、その頂点から出て行くのだが、逆戻りにも値を入れる（場合によってはその値が０になることもあるが）事になる。しかも、その逆戻りの値は負だったりもする
• 伊原のゼータ関数でサイクルのことを考えるとき、backtracklessという条件があるが、それは、逆戻りは許さないということなので、グローバー行列とは合致しない
• このような状況なので、伊原の辺接続行列とは、グローバー行列の「正の台」と呼ばれているらしい。「正の台」とは、正の値が入っているセルは１、それ以外はゼロとしたもののこと
• グローバー行列を含む、量子ウォークを表した行列の諸々は、伊原のゼータ関数よりも情報量が多い模様
• 伊原のゼータ関数は基本的には、いわゆるグラフの隣接行列の固有値が決まると、辺接続行列の固有値もそこから決まり（辺接続行列よりも小さい隣接行列の固有値で決まってしまう）、情報量としては、変わらない
• それに対して、グローバー行列は（行列サイズが同じだが、その固有値の数は、グローバー行列のサイズに依存し、そのサイズは辺接続行列のサイズと同じだが、辺接続行列の固有値がさらに小さい隣接行列の固有値で決まるのに対して、行列サイズに見合った数の固有値の情報を持つという意味で）情報量が多い
• この情報量の多さから、グラフの異同情報が増えるらしい
• ちなみに、グローバー行列の2乗の正の台にすると、それはそれで扱いに良い点が現れることもあるという

データの型・タイプ・欠測値・データの取得方法

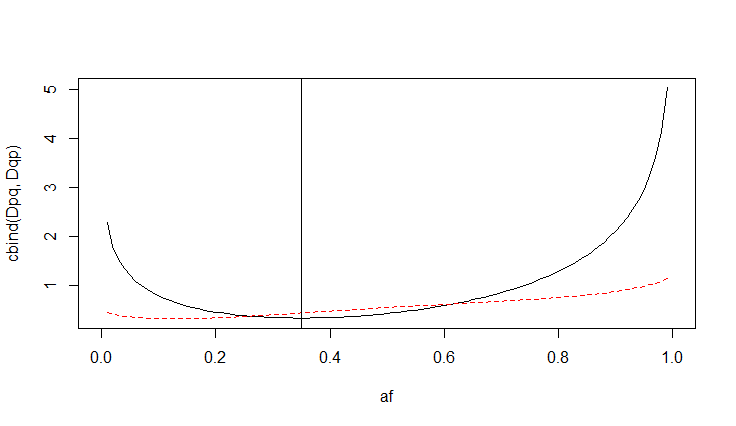
KLd(Q||P) vs KLd(P||Q)

• Some information is here

wiseodd.github.io

• genotype frequency estimation under the restiction of HWE :

.

ぱらぱらめくる『エントロピーの幾何学』

エントロピーの幾何学 （シリーズ 情報科学における確率モデル　5） [ 田中 勝 ]

目次

• まえがき
• 第１章　本書の構成
• 第２章　測度と確率
• 第３章　アファイン空間
• 第４章　経路順序確率
• 第５章　縮約と計量
• 第６章　くり込みとエントロピー
• 第７章　情報幾何学におけるq-正規分布
• 第８章　アファイン構造の多重性
• 第９章　非加法的エントロピー
• 第１０章　加法的エントロピーへの変換
• 第１１章　ホログラフィー原理
• 第１２章　平均

まえがき

• 指数型分布族だけでなく非指数型分布族が実用上重要な場面が出てきた。また、非指数型分布族を使ってもうまく動くモデル・アルゴリズムの整備も進んできた
• 非指数型分布族を利用した手法を理解するために、測度論的確率論は必要。パラメトリックモデルと十分統計量もわかっておきたい
• 指数型分布族を用いた確率モデルには情報幾何があり、そこには、二重平坦座標系がある
• 非指数型分布族についてはこれだという幾何学は定まっていない
• 非指数型分布族の幾何学の例として情報幾何学と称するものを紹介するのが本書の目的
• 情報幾何学ではというパラメタが重要で双対接続と関係する
• そのと対応するのがだが、このは確率分布族を決定し、エントロピーとダイバージェンスも決定する

第１章　本書の構成

• 第２章：測度論的確率論の基本、その用語の確認
• 第３章：測度空間に平行移動を導入。アファイン構造を持たせる。非指数型分布族が扱えることが見えてくる。BodyとSoulという概念を導入
• 第４章：平行移動導入の副作用である、測度の大きさの非保存に対して、平行移動のやり方によって座標の更新のやり方を調整するという方法を使う
• 第５章：BodyとSoulからRealを導く「縮約」操作。Fisher計量が導かれる
• 第６章：エントロピーを定義する。くり込みを用いて定義する。いわゆる情報幾何学ではエントロピーが指数型分布族のポテンシャル関数と密接な関係にあることにも特徴があるが、情報幾何学では、エントロピーをべき型拡張してあり、ポテンシャルとの関係が変わってくる
• 第７・８章：具体例。q-正規分布
• 第９章：べき型の対数関数とその性質
• 第１０章：エントロピーを共形エントロピーとしてとらえて、いわゆるエントロピーと異なる振る舞いをしているものを、扱う方法を説明する
• 第１１章：エントロピーの扱いで用いたスケール変換で用いるパラメタを座標とみなすことで、ホログラフィー原理としてとらえる
• 第１２章：一般化平均としての平均

第２章　測度と確率

• 試行、事象、根源事象、全事象、空事象、加法族、可測関数、確率変数、可測空間、測度、測度空間、ボレル加法族、ルベーグ測度
• 集合があって、どのように足し合わせをするかの位相があると、可測空間。そこにここはこのくらいの重みがあるよ、という測度を入れると測度空間になる

第３章　アファイン空間～積・商・指数関数・対数関数の一般化

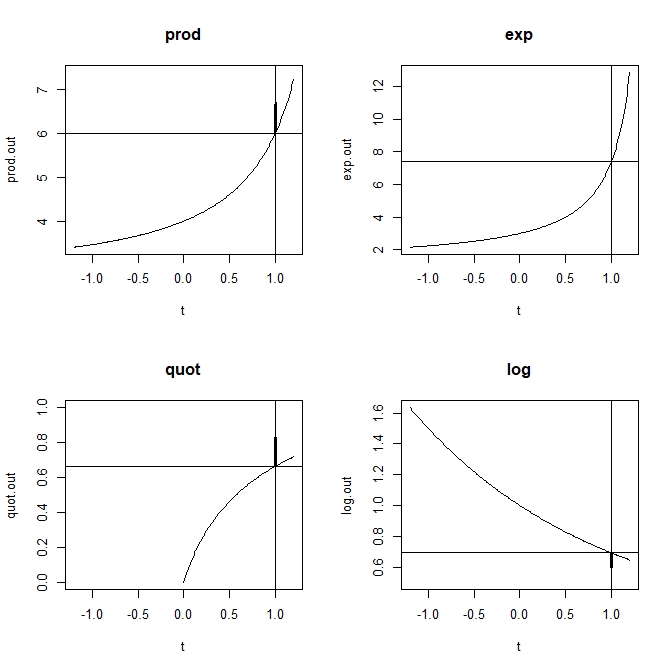
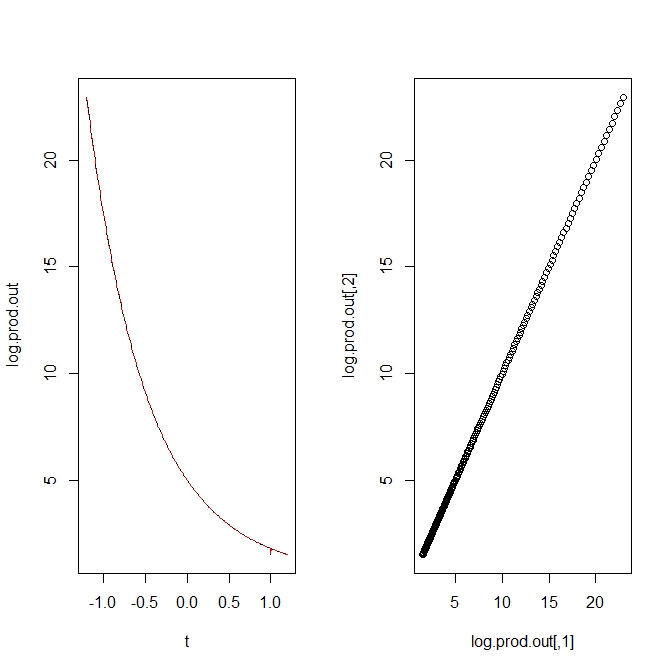
• 演算の冪型拡張
  • 積は
    • 普通の積は、の場合。極限として定義される(があるから
  • 商(f/gに対応する商)は
  • 指数関数は
  • 対数関数は
    • 指数関数の積は１通りだが、対数関数の積は２通りの表現を持つ(が、値は同じ？）
      • 
      • 
    • この非１通り性が、エントロピーの非加法性の素になる

• アファイン構造
  • いわゆるアファイン空間は、集合にベクトルを加える操作を許して作る空間。加えるベクトルたちはいわゆるベクトル空間をなしている
  • ベクトルを加えることを平行移動と言う。平行移動した先も、元の集合の要素
  • 集合の要素にベクトルを加えることで任意の集合の要素に移動できるようにすれば、集合のすべての要素は、ある一つの要素とベクトルとの和としみなせる
  • ベクトル空間の部分空間によって移動できる要素は、元の集合の部分集合。これがアファイン部分空間
  • 平行移動(ベクトルを加える)と言ってきたが、実際には、ベクトルによる平行移動として、冪型拡張した指数関数()を掛ける(冪型積をとる)こととする(いかにも、「確率密度分布、指数型分布族の拡張っぽい話になってきた)
  • 平行移動した後、測度の変化が起きるが、それを座標の変化に吸収させる操作などを使う
• 尤度関数、対数尤度関数、スコア関数(対数尤度関数の偏微分)も、冪型拡張の仕掛けで記載が可能になる
• アファイン構造とその共役空間としてアファイン構造というものを定めると、両者には双対空間と言う関係が
• この共役関係・双対関係の片方にSoul、もう片方にBodyと言う名前がついている
• SoulとBodyとを縮約操作するとRealと言うものが現れるという

第４章　経路順序確率

• アファイン構造では、始点と終点が決まると平行移動量が一意に決まる
• そのベクトルに沿った経過点を経た多段階平行移動という概念もありえる
• 確率分布を指定する座標の変換ルールとして、経路上の逐次変換が定められることが示せる

第５章　縮約と計量

• 共役関係にあるSoulとBodyでの量を単純に掛けて、確率変数について積分すると、通常の意味でのFisher 情報量が出る
• この演算を縮約と定義する
• この定義によって得られるFisher計量には、ミンコフスキーの行列のように、負の対角成分が現れる

第６章　くりこみとエントロピー

• 通常のエントロピーは負の対数尤度の期待値
• くり込みは計算結果が無限大に発散してしまうのを防ぐ数学的な技法であり、場の量子論で使われる
• くり込みを使って、アファイン構造でのエントロピーの発散を抑える
• BodyとSoulとがあるので、エントロピーもそれぞれに定まる
• ダイバージェンスもBodyとSoulとでそれぞれ定まる
• ダイバージェンスは確率分布間の平行移動量に関する２次以上の近似誤差として表現される(分布を平行移動したらそのまま同じであってもよいはずだが、分布が形を変える。その変化量の１次の差は(多分、平行移動そのものがもたらす違いなので)分布の違いには影響せず、分布としての違いは２次以上の差となる、という話なのだろう

第７章以降、省略