フェノタイプの整理メモ１３ 確率的に考える８

• 一過性か慢性か
  • 活動性病変の成立に複数ステップを要し、逆行プロセスがあるとしても、その逆行プロセスの性質によって、活動病変の不活動化や再発には違いが生じるだろう
  • 逆行プロセスの起動感度が低い(ある程度の活動状態(病変として観察されるよりは低い状態も含め)があって初めて起動するような場合)には、逆行プロセスの起動により、活動性病変はいったんおさまるものの、「くすぶった状態」までしか逆行させられないので、再び、活動性病変化する可能性が高い
    • 起動こそ、感度が悪いが、逆行プロセス自体は十分な逆行力があれば、寛解・再燃を繰り返しそうである

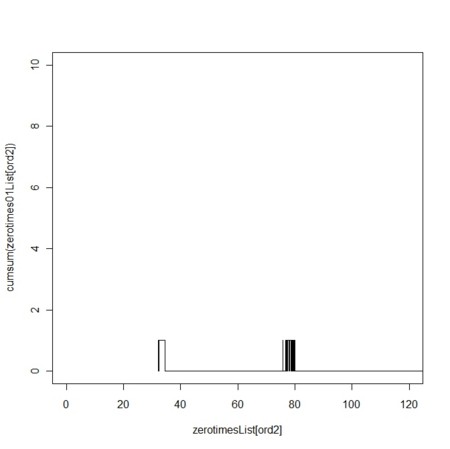
• • 逆行プロセスの逆行力が弱い、逆行プロセスの起動頻度が乏しいような場合には、一度、進んでしまうと、なかなか良い状態に戻すことができないので、遷延化しやすそうである

# 数えられるフェノタイプ

# 3ジェノタイプを比較する

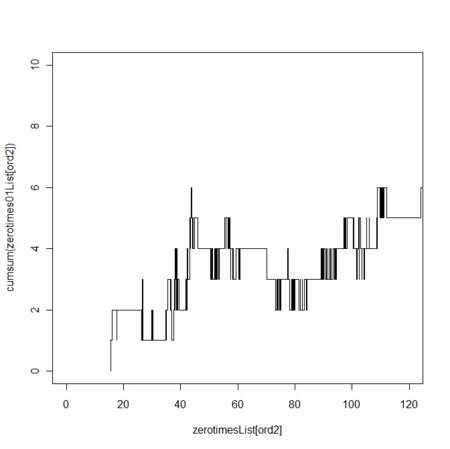
NL<-1 # 座位数
TL<-120 # 一生は120年

# イベントがしょっちゅう起きて(均質化して)いる場合には
# Dxのタイミングにはばらつきが小さい

Fs<-0.01*2^(10) # イベントが起きる平均時間間隔(年)

#GsRatios<-seq(from=0.8,to=2,length=10)

# 寛解・再燃：Gs=1.05 ControlThres=49
# 慢性化：Gs=0.9 ControlThres=30

GsRatios<-c(1.05)
par(ask=TRUE)
for(gi in 1:length(GsRatios)){
	
Gs<-Fs*GsRatios[gi] # イベントを修復する平均時間間隔(年)

ThresNums<-c(50)
ControlThres<-49 # 逆行プロセスキックイン閾値
Nlegion<-10 # 関節数とか

Niter<-1 # 人数

for(fi in 1:length(Fs)){
	F<-Fs[fi]
	G<-Gs[fi]
	for(ti in 1:length(ThresNums)){
		ThresNum<-ThresNums[ti]
		for(ii in 1:Niter){
			NR<-ThresNum*1000
			Fevents<-matrix(rexp(Nlegion*NR,F),nrow=Nlegion)
			Gevents<-matrix(rexp(Nlegion*NR,G),nrow=Nlegion)
			FeventsCum<-t(apply(Fevents,1,cumsum))
			GeventsCum<-t(apply(Gevents,1,cumsum))
			
			FGtime<-cbind(FeventsCum,GeventsCum)
			FG11<-cbind(matrix(1,nrow=Nlegion,ncol=NR),matrix(-1,nrow=Nlegion,ncol=NR))
			zerotimesList<-c()
			zerotimes01List<-c()
			for(i in 1:Nlegion){
				ord<-order(FGtime[i,])
				tmp11<-FG11[i,ord]
				tmpcumsum<-cumsum(tmp11)
				truecumsum<-tmpcumsum
				
				negs<-which(tmpcumsum<ControlThres)
				if(length(negs)>0){
					negval<-tmpcumsum[negs]
					maxNeg<-min(negval)
					inits<-rep(0,abs(maxNeg))
					for(j in 1:length(inits)){
						inits[j]<-which(negval==-j)[1]
					}
					cancelled<-FG11[i,ord]
					cancelled[negs[inits]]<-0
					
					truecumsum<-cumsum(cancelled)
				}
				truecumsum01<-truecumsum-ThresNum
				zeros<-which(truecumsum01==0)
				if(length(zeros)>0){
					zerotimes<-FGtime[i,ord[zeros]]
					zerotimes01<-(-1)^(0:(length(zerotimes)-1))
					zerotimesList<-c(zerotimesList,zerotimes)
					zerotimes01List<-c(zerotimes01List,zerotimes01)
				}
				
				
#matplot(cbind(tmpcumsum,truecumsum),type="l")
			}
			ord2<-order(zerotimesList)
			#if(min(cumsum(zerotimes01List[ord2]))<0){
			plot(zerotimesList[ord2],cumsum(zerotimes01List[ord2]),type="s",xlim=c(0,TL),ylim=c(0,Nlegion))
			#plot(zerotimesList[ord2],(zerotimes01List[ord2]),type="s",xlim=c(0,TL),ylim=c(0,Nlegion))

			#}
		}
	
	}

}

}