2011-10-30

情報を利用する

R 尤度

こちらの続き
こんな状況を考える
- 夕闇迫るある日、「泥棒！」という叫び声とともに走り去る後姿が
- そこは、ある小学校の前の道だった
- 小学校には下校しようとしていた複数の小学生がいた
- 目撃者情報を募ったところ
- 走り去ったのは男だった、という意見が６人、女だったという意見が４人、だったと言う
- さて、容疑者が男女取り混ぜて何人かが挙がったところで、この小学生の目撃情報はどのように使うのか
  - 容疑者の性別に照らして、容疑者を真犯人とみなす尤度はどのように上げ下げすればよいのだろうか？
- 同じ状況で、男だったという意見が６００人、女だったという意見が４００人だったら、どうなるのだろう
- そもそも、６：４と６００：４００では、どちらが、性別を確定的にしてくれる情報なのだろうか？
- ６００：４００の場合、「男と言う答が得られる確率の最尤推定値は0.6で、その信頼区間は極めて狭い」ということになるのだが、それは、「男か女か判断しにくい条件だったということを強く示唆しており、男女情報の信ぴょう性を弱める力が強い」という性格がある一方で、確かに、男意見が「圧倒的に」女意見より大きいという性格もある。これの総合判定がしたい
モデル
- 今、真犯人が男であるときに、それを目撃して、男と正しく答える確率をp、間違えて女と答える確率を1-pとする
- 逆に、真犯人が女であるときに、性別を正しく答える確率と誤答する確率は、やはりp,1-pであるとしよう
- このようなときに、総数N人の答があって、その内訳がNm+Nf=N(Nmは男、Nfは女と答えた人数)であるとすると
- 真犯人が男である仮説の尤度は $L(m)=\begin{pmatrix}N\\Nm\end{pmatrix}p^{Nm}(1-p)^{Nf}$
- 真犯人が女である仮説の尤度は
  - 4人対8人の場合

- - 40人対80人の場合

- つまり、間違い確率1-pがわかっていれば、男説、女説の尤度の計算ができる
- では、pはいくつなのか
- 今、男であるという事前確率がq、女であるという事前確率が1-qであるときに、男Nm、女Nfと答える確率っていうのは
- $Pr(p)=q\times \begin{pmatrix}N\\Nm\end{pmatrix}p^{Nm}(1-p)^{Nf} + (1-q)\times \begin{pmatrix}N\\Nm\end{pmatrix}p^{Nf}(1-p)^{Nm}$
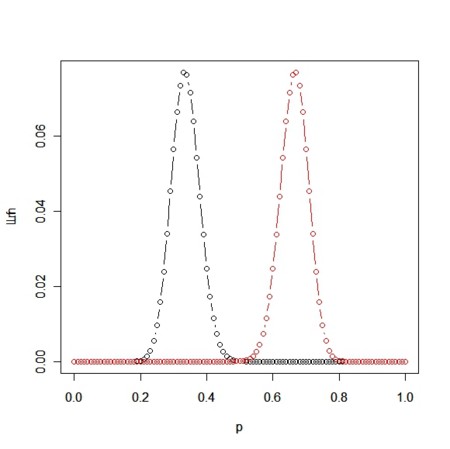
- 今、pを0から1までにしてプロットしている

- p<0.5というのは、男である場合に、女であると答える確率が男であると答える確率より大きいということである
- p<0.5は、「変装」している場合とかに限られて、『証言』としては変(変装して普通なら女に見えるように逃走したなら、目撃証言は「見え方の性別」で収集して、「変装していた証拠」を探してやるのが正攻法…)
- なので、0.5<=p<=1をpの範囲とする

- すると、目撃情報を基にして真犯人が男、女、のそれぞれの尤度は $\int_{0}^{0.5} Lm(p)*Pr(p)dp$ , $\int_{0}^{0.5} Lf(p)*Pr(p)dp$ となる
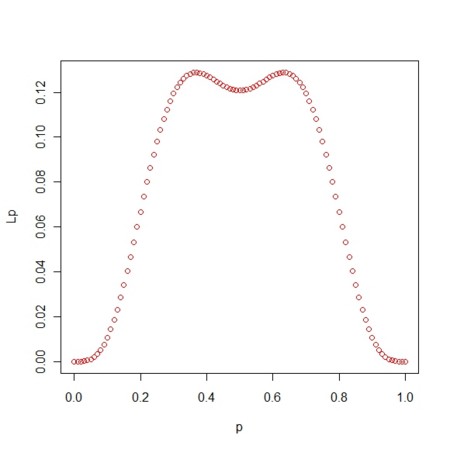
- 図で言えば、それぞれのラインの下面積

最終的に関数にすれば
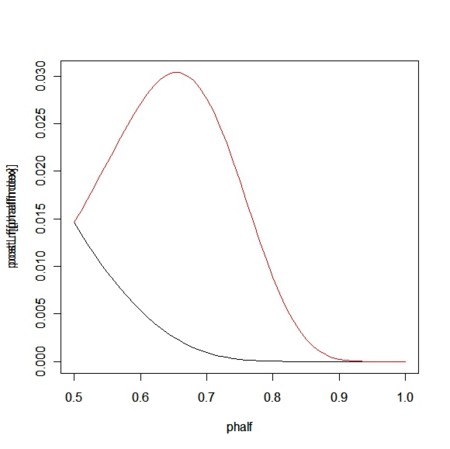
- 男女の事前確率をq,(1-q)とした上で、Nm,Nfの目撃情報を使って「真犯人は男だ仮説」と「真犯人は女だ」仮説の事後確率を出せる

# 男女別目撃情報数
Nm<-1
Nf<-6
N<-Nm+Nf
# 目撃情報が正しい確率
p<-seq(from=0,to=1,length=101)
# 男情報が正しいとき、女情報が正しいときの尤度
Lm<-choose(N,Nm)*p^Nm*(1-p)^Nf
Lf<-choose(N,Nm)*(1-p)^Nm*p^Nf
plot(p,Lm)
par(new=TRUE)
plot(p,Lf,col=2)
# 事前確率
q<-0.5
# 正答率pの尤度
Lp<-q*Lm+(1-q)*Lf
# 正答率pは0.5以上であると制約する
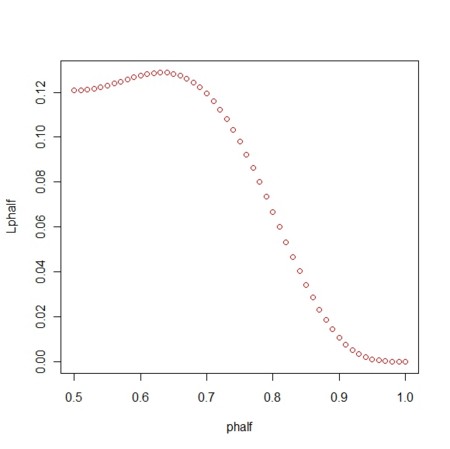
phalfIndex<-which(p>=0.5)
phalf<-p[phalfIndex]
Lphalf<-Lp[phalfIndex]
plot(p,Lp,col=2)
plot(phalf,Lphalf,col=2)
# 目撃情報の後の確率
postLm<-Lp*Lm
postLf<-Lp*Lf

ylim<-c(0,max(postLm[phalfIndex],postLf[phalfIndex]))
plot(phalf,postLm[phalfIndex],type="l",ylim=ylim)
par(new=TRUE)
plot(phalf,postLf[phalfIndex],col=2,type="l",ylim=ylim)

# 目撃情報数を10倍する
Nm<-10
Nf<-60
N<-Nm+Nf

p<-seq(from=0,to=1,length=101)

Lm<-choose(N,Nm)*p^Nm*(1-p)^Nf
Lf<-choose(N,Nm)*(1-p)^Nm*p^Nf

plot(p,Lm,type="b")
par(new=TRUE)
plot(p,Lf,col=2,type="b")
# 事前確率
q<-0.5
# 正答率pの尤度
Lp<-q*Lm+(1-q)*Lf


phalfIndex<-which(p>=0.5)
phalf<-p[phalfIndex]
Lphalf<-Lp[phalfIndex]
plot(p,Lp,col=2)
plot(phalf,Lphalf,col=2)

postLm<-Lp*Lm
postLf<-Lp*Lf

ylim<-c(0,max(postLm[phalfIndex],postLf[phalfIndex]))
plot(phalf,postLm[phalfIndex],type="l",ylim=ylim)
par(new=TRUE)
plot(phalf,postLf[phalfIndex],col=2,type="l",ylim=ylim)

こちらに続く