遺伝子影響の連続スペクトラム化

• こちらで体細胞モザイクのことを書いた
• こちらで複合遺伝性疾患の説明をするためにも、少し言及する(予定)
• もう少し一般的に、変異・機能発現について一般化して考えようと思う
• 個体のゲノム
  • (1) 個体としてのヒトができる前の段階に２つの配偶子がある(ハプロイドｘ２）
  • (2) ２つの配偶子が合わさってできる受精卵ができる(ディプロイドｘ１）
  • (3) 受精卵は分裂する(ディプロイドｘ)
  • (4) 細胞は分化する。細胞には死ぬものもある。細胞には増殖能を持つものもあれば、持たないものもある(ディプロイドｘ)
  • (5) すべての細胞はなにかしらの機能を有し、その機能は細胞単位のフェノタイプとみることができる
  • (6) 複数の細胞の機能を合算して観察し、それをフェノタイプととらえることもある
  • (7) 個体レベルで観察できるフェノタイプもある
  • (8) フェノタイプがいろいろに変化する
  • (9) 個体死というフェノタイプを持って、個体は消滅する
  • (10) 個体は消滅する前に、複数の配偶子を算出しうる(ハプロイドｘNg)
  • (11) 配偶子は他の個体の配偶子と合わさって受精卵(ディプロイドｘ１)を作ることがある
• 個体の持つ変異アレル
  • (1) 配偶子の持つ変異の割合と分布(ハプロイド単位で２個ｘ(0/1))
  • (2) 受精卵の持つ変異の割合と分布(ディプロイド単位で１個ｘ0/0.5/1)
  • (3) 卵割途中での変異(ディプロイド単位で個は(0)と１個は(1)。(0)/(1)の比が
  • (4) 卵割が進むと(ディプロイド単位で個は(0)、個は(1)。(0)/(1)の比が
  • (5) この先は、少し複雑だが、考え方は同じ
• １座位の変異アレルとフェノタイプ
  • ２個の配偶子のうち２個がそろって持つ変異アレルは、個体のすべてのディプロイドを(1)とする。これをフェノタイプ発現の条件とする場合、そのフェノタイプは劣性遺伝形式
  • ２個の配偶子のうち１個が持つ変異アレルは、個体のすべてのディプロイドを(0.5)とする。これをフェノタイプの発現の条件とする場合、そのフェノタイプは優性形質
  • 受精卵となったのちに生じた変異アレル(体細胞変異アレル)は、個体の一部の細胞に保有される。保有の形式は多くの場合、(0.5)である。このような変異アレルがフェノタイプの発言条件を決める場合には、保有細胞数・保有細胞タイプの影響を受ける(はず)
• 複数座位の変異アレルとフェノタイプ
  • 配偶子由来の変異アレルと体細胞変異アレルとが共存する
  • 共存の仕方は、細胞の中で共存する場合と、異なる細胞に分かれて共存する場合とがあり、それぞれ、保有細胞数・保有細胞タイプとで分類することができる
  • 同一細胞に共存する場合は、細胞単位でのフェノタイプが形成され、それがひいては個体レベルのフェノタイプとして観察される。特に増殖力が強いこと・個体致死機能が強いことを持って悪性腫瘍と言う
  • 異なる細胞が別の変異アレルを保有しそのために、個々の細胞のフェノタイプがどう変わり、複数の細胞が形成するフェノタイプがどう変わるかについては(おそらく、明らかな例はないのではないかと思われるが(不勉強なので、知らないだけかもしれない)、おそらく存在するだろう
• 複数個体の変異アレルとフェノタイプ
  • 細胞のジェノタイプとそのフェノタイプ、異なるジェノタイプを持つ細胞の集合としての細胞集合(個体を含む)とそのフェノタイプとについて言及した
  • 個体の集合を考えるとき、個体が集団となることで観測できるフェノタイプ(集団フェノタイプ)を考えよう
  • そのときには、変異アレルが保有個体数・保有個体タイプ、個々の個体での保有細胞数・保有細胞タイプ、とが影響する、というように、階層化して考えることができる
  • これよりさらに階層を登ることができる？できる。集団の集合(「個体の集合を家族、家族の集合を地域」、「個体の集合をくに、くにの集合を国家連合」…
• そんなことをRでやってみる
  • 受精卵から卵割を開始する
  • ２分割を繰り返す
  • ２分岐木ができる
  • 系列ごとに分割までの時間をばらつかせる
  • 特定の時刻において、２分岐木のどこのノードが「存在しているか」が変遷する
  • 分割の過程で変異がおきる
  • 変異は継承される
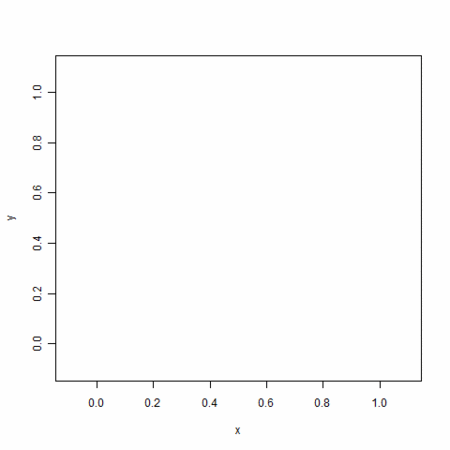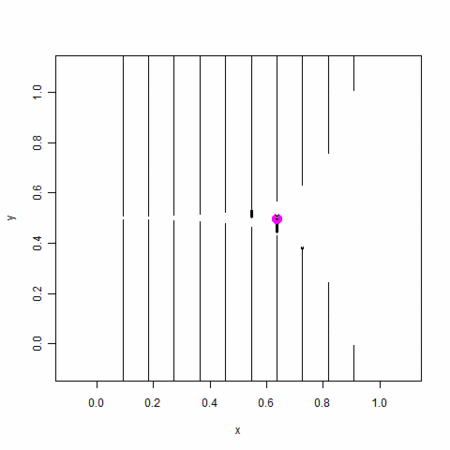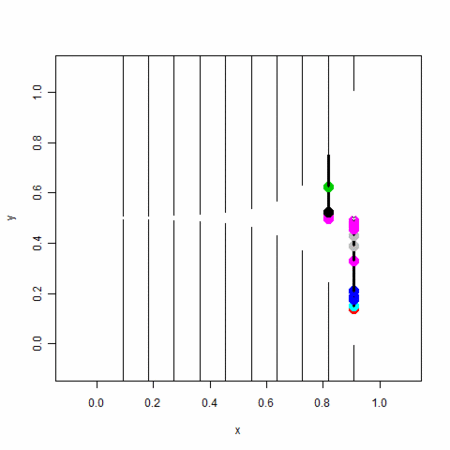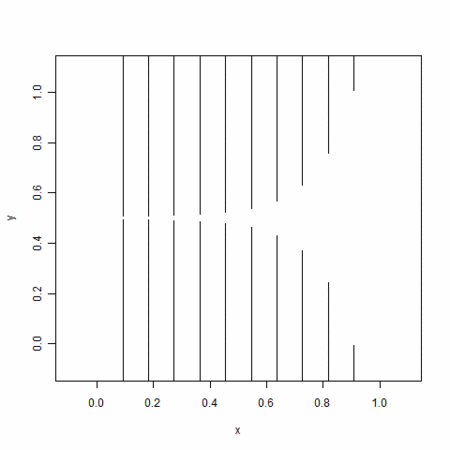
  • わかり易いように分岐の速い細胞が下方向に来るようにしてある
  • 入った変異が強調されるように、大きな点で打つとともに、入った変異ごとに色を変えている

cell<-function(period=NULL,from=NULL,to=NULL,prof.rate=NULL,id=NULL,gen=NULL,gen.id=NULL,mut=NULL){
	
	list(period=period,from=from,to=to,prof.rate=prof.rate,id=id,gen=gen,gen.id=gen.id,mut=mut)
}
Ngen<-10
minT<-0
maxT<-0
Cells<-list()
counter<-1
mut.counter<-0
mut.rate<-0.01
#gen.counter<-1
for(i in 1:Ngen){
	gen.counter<-1
	tmpCells<-list()
	Cells[[i]]<-list()
	Tos<-c()
	for(j in 1:2^(i-1)){
		mut<-0
		if(runif(1)<mut.rate)mut<-1	
		mut.counter<-mut.counter+1
		if(i==1){
			tmp.period<-runif(1)
			tmp.from<-0
			tmp.to<-tmp.from+tmp.period
			tmp.mut<-NULL
			tmp.prof.rate<-1+0.01*runif(1)
			if(mut==1)tmp.mut<-mut.counter
			tmpCells[[j]]<-cell(period=tmp.period,from=tmp.from,to=tmp.to,prof.rate=tmp.prof.rate,id=counter,gen=i,gen.id=gen.counter,mut=tmp.mut)
			counter<-counter+1
			gen.counter<-gen.counter+1
			Tos<-c(Tos,tmpCells[[j]]$to)
			if(maxT<tmpCells[[j]]$to)maxT<-tmpCells[[j]]$to
		}else{
			prnt<-ceiling(j/2)
			parent<-Cells[[i-1]][[prnt]]
			tmp.period<-parent$period+runif(1)
			tmp.from<-parent$to
			tmp.to<-tmp.from+tmp.period
			tmp.mut<-parent$mut
			tmp.prof.rate<-1+0.01*runif(1)
			if(mut==1)tmp.mut<-c(tmp.mut,mut.counter)
			tmpCells[[j]]<-cell(period=tmp.period,from=tmp.from,to=tmp.to,prof.rate=tmp.prof.rate,id=counter,gen=i,gen.id=gen.counter,mut=tmp.mut)
			counter<-counter+1
			gen.counter<-gen.counter+1
			Tos<-c(Tos,tmpCells[[j]]$to)

			if(maxT<tmpCells[[j]]$to)maxT<-tmpCells[[j]]$to
		}
		
	}
	ord.to<-order(Tos)
	for(k in 1:length(ord.to)){
		Cells[[i]][[k]]<-tmpCells[[ord.to[k]]]
	}
}

par(ask=TRUE)
x<-y<-0
xlim<-ylim<-c(-0.1,1.1)
plot(x,y,xlim=xlim,ylim=ylim,col=0)
Nt<-100
Ts<-seq(from=minT,to=maxT,length=Nt)
sleep<-0.05
for(tt in 1:(length(Ts))){
	plot(x,y,xlim=xlim,ylim=ylim,col=0)

	for(i in 1:length(Cells)){
		tmpx<-i/(length(Cells)+1)
		abline(v=tmpx)
		for(j in 1:length(Cells[[i]])){
			tmpy<-(j-length(Cells[[i]])/2)/length(Cells[[length(Cells)]])+0.5
			col<-0
			cex<-0.5
			if(Cells[[i]][[j]]$from<=Ts[tt] & Cells[[i]][[j]]$to >Ts[tt]){
				col<-1
				#cex<-cex*Cells[[i]][[j]]$prof.rate^(Ts[tt]-Cells[[i]][[j]]$from)
				if(length(Cells[[i]][[j]]$mut)>=1){
					col<-col+max(Cells[[i]][[j]]$mut)
					cex<-2*cex*2^length(Cells[[i]][[j]]$mut+1)
				}
			}
			points(tmpx,tmpy,cex=cex,col=col,pch=16)
		}
	}
	#Sys.sleep(sleep)
}

# 画像送りの間隔をintervalで指定してある
par(ask=FALSE)
library(animation)
saveGIF({
x<-y<-0
xlim<-ylim<-c(-0.1,1.1)
plot(x,y,xlim=xlim,ylim=ylim,col=0)
Nt<-100
Ts<-seq(from=minT,to=maxT,length=Nt)
sleep<-0.05
for(tt in 1:(length(Ts))){
	plot(x,y,xlim=xlim,ylim=ylim,col=0)

	for(i in 1:length(Cells)){
		tmpx<-i/(length(Cells)+1)
		abline(v=tmpx)
		for(j in 1:length(Cells[[i]])){
			tmpy<-(j-length(Cells[[i]])/2)/length(Cells[[length(Cells)]])+0.5
			col<-0
			cex<-0.5
			if(Cells[[i]][[j]]$from<=Ts[tt] & Cells[[i]][[j]]$to >Ts[tt]){
				col<-1
				#cex<-cex*Cells[[i]][[j]]$prof.rate^(Ts[tt]-Cells[[i]][[j]]$from)
				if(length(Cells[[i]][[j]]$mut)>=1){
					col<-col+max(Cells[[i]][[j]]$mut)
					cex<-2*cex*2^length(Cells[[i]][[j]]$mut+1)
				}
			}
			points(tmpx,tmpy,cex=cex,col=col,pch=16)
		}
	}
	#Sys.sleep(sleep)
}
},interval=0.05)