距離の分布を調べる

• 書きかけ！
• まず、1次元空間の分布を考える

library(sde)
library(ggplot2)
Npt<-1000
d <- expression(5)
s <- expression(3)
X <- data.frame(x=c(sde.sim(X0=0,drift=d,sigma=s,N=Npt-1)))
#gp <- ggplot(data=X,aes(x=x)) + geom_bar()
# 平均値を縦線で示す
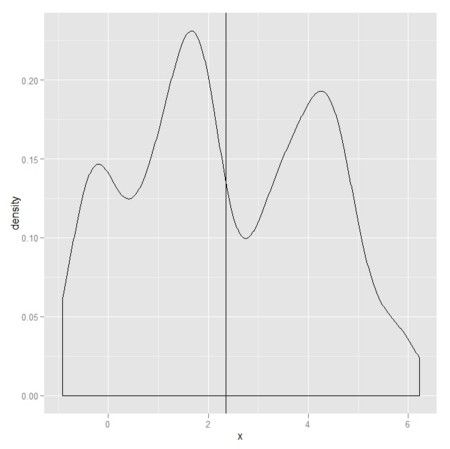
gp <- ggplot(data=X,aes(x=x)) + geom_density() + geom_vline(xintercept = mean(X$x))
gp

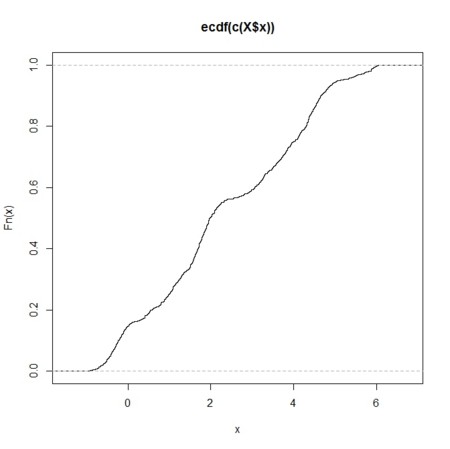
• 累積分布も取れる
  • 累積分布と確率密度分布との関係は、お互いの微分と積分の関係(傾きと下面積)

X.ecdf <- ecdf(c(X$x))
plot(X.ecdf)

• ある値において、累積分布のある方向への増加率は、その値における密度
• 同じ値において、逆方向への増加率は、やはりその値における密度
• したがって、ある値における密度は、「どちらの方向」でも増加率を表している
• では、方向を無視する(距離にする)とどうなる？？
  • 平均値で折り返し、その値を新たに0とする
  • 平均値の前後では、xが小さくなると確率が増え、xが大きくなると確率が減るが、その増減は相互に埋め合わすような関係にある
  • そのため、平均値で折り返した後の「密度分布」

# ある値x
x <- mean(X$x)
X.1 <- data.frame(x=c(X$x[which(X$x>=x)]-x,x-X$x[which(X$x<x)]))
# 折り返し
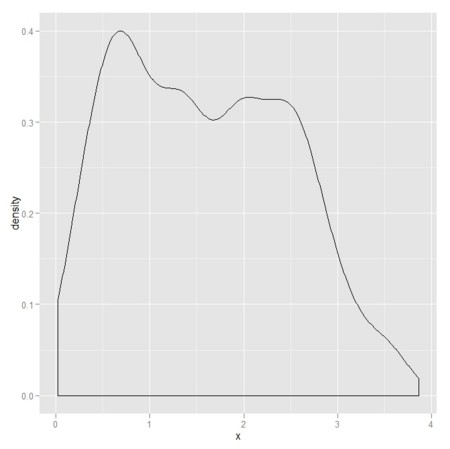
gp.1 <- ggplot(data=X.1,aes(x=x)) + geom_density() 
gp.1
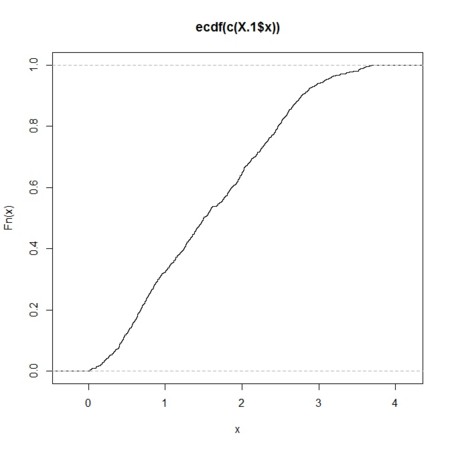
X.1.ecdf <- ecdf(c(X.1$x))
plot(X.1.ecdf)