- あれか、これか、型の検査や情報というものを考える
- 「吐物の色が赤か茶色か」
- 「アレルがAかaか」
- 「光学異性体のD体かL体か」など
- その前に、検査学の復習をしておこう
- ある疾患の検査前事前確率がpであり、ある検査があって、その感度がu、特異度がv であるとき
| test(+) | test(-) |
---------------------------------------------
D(+) | pu | p(1-u) | p
D(-) | (1-p)(1-v) | (1-p)v | 1-p
---------------------------------------------
| 1-(p+v) + p(u+v) | (p+v) - p(u+v) | 1
-
- 検査陽性(test(+))であったなら、疾患である事後確率は pu/(1-(p+v) + p(u+v)) になり、疾患でない事後確率は (1-p)(1-v)/ (1-(p+v) + p(u+v)) になる
- 検査陽性(test(-))であったなら、疾患である事後確率は p(1-u)/( (p+v) -p(u+v) ) になり、疾患でない事後確率は (1-p)v/( (p+v) - p(u+v) )になる
- あれか、これか、の検査
- 光学異性体のD体かL体かの検査のような場合を考える
- D体らしさの検査をして、「らしかったら」D体と判断して「らしくなかったら」L体と判断するというやり方もあるだろう。この場合は、上の病気の検査と同じ
- そうではなくて「D体らしかったら」Dに相当するシグナルが返り、「L体らしかったら」Lにそうとうする シグナルが返る、というような検査も可能だろう。ここでDとLはごく対称的なものであるから、その検査特性もよく似ているとする
- このとき、u=v
| test(+) | test(-) |
-------------------------------------------------
D(+) | pu | p(1-u) | p
D(-) | (1-p)(1-u) | (1-p)u | 1-p
-------------------------------------------------
| pu + (1-p)(1-u) |1-(pu + (1-p)(1-u)) | 1
-
- このようなとき、事前確率pが検査後、pu/(pu+(1-p)(1-u)) に変わるか、p(1-u)/(1-(pu+(1-p)(1-u)))に変わる
ps <- seq(from=0,to=1,length=51)
ps <- ps[-1]
ps <- ps[-length(ps)]
us <- ps
pus <- as.matrix(expand.grid(ps,us))
p <- pus[,1]
u <- pus[,2]
post.1 <- p*u/(p*u+(1-p)*(1-u))
post.2 <- p*(1-u)/(1-(p*u+(1-p)*(1-u)))
fold.1 <- post.1/p
fold.2 <- post.2/p
image(matrix(fold.1,length(ps),length(us)))
library(rgl)
plot3d(cbind(pus,log(fold.1)))
open3d()
plot3d(cbind(pus,log(fold.2)))
- uが高くないと採用しないとすると
- 確率を高める方は、たかだか、1/p 倍にしかならないので、1 〜 1/p倍を変化するだけだが
- 確率を低める方は、1 倍から、確率0へと指数関数的に確率を下げるので、
- uを採用する基準を厳しくすると、それだけ確率を小さくする機会を取り除いてしまうことになる
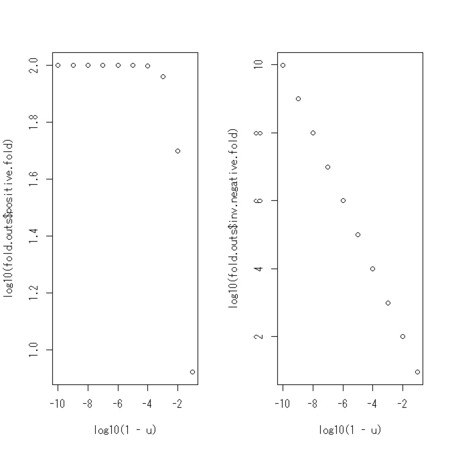
fold.change <- function(p,u){
return(list(positive.fold = u/(p*u+(1-p)*(1-u)),negative.fold = (1-u)/(1-(p*u+(1-p)*(1-u))),inv.negative.fold = 1/((1-u)/(1-(p*u+(1-p)*(1-u)))) ))
}
fold.change(0.01,0.95)
p <- 0.01
u <- 1-(0.1^(1:10))
fold.outs <- fold.change(p,u)
par(mfcol=c(1,2))
plot(log10(1-u),log10(fold.outs$positive.fold))
plot(log10(1-u),log10(fold.outs$inv.negative.fold))
par(mfcol=c(1,1))
