- こちらでポアソン分布を気にしている
- その続き
- L回の観察機会のうち、
 ([tex:k<
([tex:k<
- この事象をN回観察する機会があったら、何回起きると予想するのだろうか?
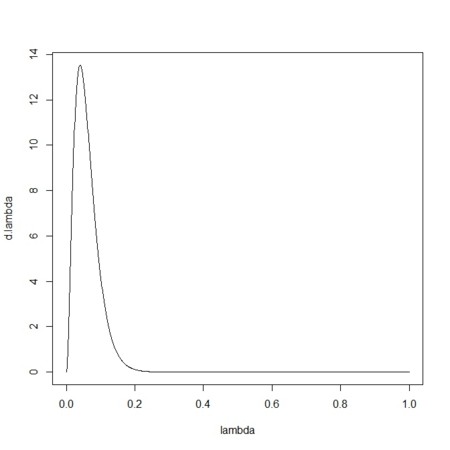
- L回の観察、k回の生起、から、ポアソン分布のパラメタ
 の確率密度分布を、ガンマ分布として推定することにする
の確率密度分布を、ガンマ分布として推定することにする
- ガンマ分布を選ぶのは、ポアソン分布の共役事前分布だから
L <- 50
k <- 3
lambda <- seq(from=0,to=1,length=1000)
d.lambda <- dgamma(lambda,k,L)
plot(lambda,d.lambda,type="l")
- いろいろな
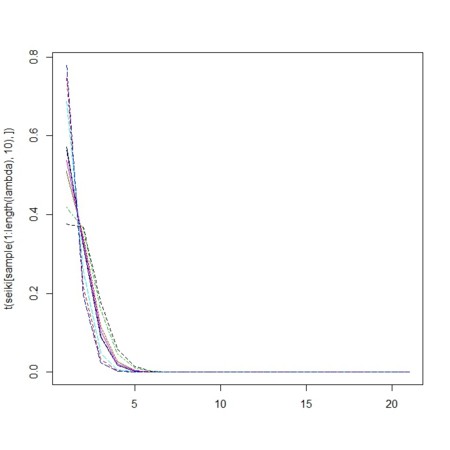
 について、N回の観察をしたときにt回生起する確率はポアソン分布に従う
について、N回の観察をしたときにt回生起する確率はポアソン分布に従う
N <- 200
t <- 0:20
seiki <- matrix(0,length(lambda),length(t))
for(i in 1:length(lambda)){
seiki[i,] <- dpois(t,lambda[i])
}
apply(seiki,1,sum)
matplot(t(seiki),type="l")
matplot(t(seiki[sample(1:length(lambda),10),]),type="l")
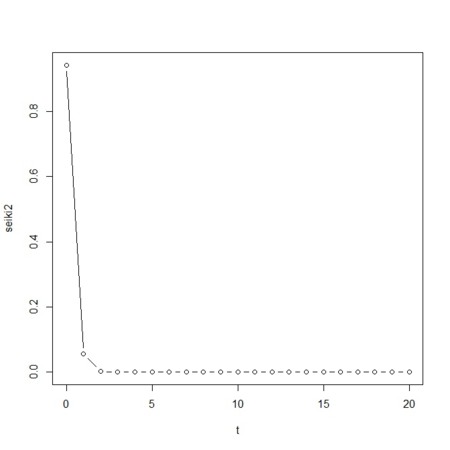
 の値を適当に細かくとって、それぞれの
の値を適当に細かくとって、それぞれの の値に上で求めた、確率の重みをつければ、N回の観察でt回の生起が起きる確率を求めることができる
の値に上で求めた、確率の重みをつければ、N回の観察でt回の生起が起きる確率を求めることができる
x <- matrix(0,length(lambda),length(t))
for(i in 1:length(lambda)){
x[i,] <- d.lambda[i] * seiki[i,] * (lambda[2]-lambda[1])
}
sum(x)
seiki2 <- apply(x,2,sum)
plot(t,seiki2,type="b")
 の値を連続的にとって、その全部について
の値を連続的にとって、その全部について の確率に応じて積分しよう
の確率に応じて積分しよう の確率密度分布を[tex:G(k+a,L+b) = \frac{\lambda^{(k+a)-1}exp(-(L+b)\lambda)}{\Gamma*1(\frac{1}{(L+b)})^k}]と推定することにする
の確率密度分布を[tex:G(k+a,L+b) = \frac{\lambda^{(k+a)-1}exp(-(L+b)\lambda)}{\Gamma*1(\frac{1}{(L+b)})^k}]と推定することにする のポアソン分布でN回の観察をすれば、
のポアソン分布でN回の観察をすれば、 回の生起が期待されるから、t回生起する確率は
回の生起が期待されるから、t回生起する確率は
- 両方の分布を
 について積分すればよいから
について積分すればよいから
 が知りたい確率
が知りたい確率 - [tex:G(k+a,L+b)P(N,\lambda) = \frac{\lambda^{(k+a)-1}exp(-(L+b)\lambda)}{\Gamma*2(\frac{1}{(L+b)})^k}\frac{(N\lambda)^t}{t!}exp(-N\lambda)]
- [tex:\frac{N^t}{\Gamma*3(\frac{1}{L+b})^k t!} \lambda^{k+a+t-1} exp(-(L+b+N)\lambda)]
- ここで
 について考える
について考える
- これを用いると

- [tex:=\frac{N^t}{\Gamma*4(\frac{1}{L+b})^k t!} \Gamma(k+a+t) (\frac{1}{L+b})^{k+a+t}]
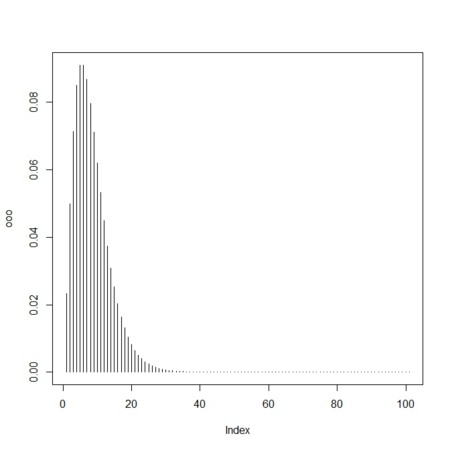
my.fromgammatopois <- function(N,ts,k,theta){
ps <- (k+ts-1)
q <- -(N+theta)
exp(ts*log(N)-lgamma(k)-k*log(1/theta)-lgamma(ts+1) + lgamma(ps+1) - (ps+1)*log(-q))
}
a <- 1
b <- 1
k <- 2
L <- 39
N <- 100
t <- 0:100
ooo <- my.fromgammatopois(N,t,k+a,L+b)
plot(ooo,type="h")
sum(ooo)
([tex:k<
の確率密度分布を、ガンマ分布として推定することにする
について、N回の観察をしたときにt回生起する確率はポアソン分布に従う
の値を適当に細かくとって、それぞれの
の値に上で求めた、確率の重みをつければ、N回の観察でt回の生起が起きる確率を求めることができる
の値を連続的にとって、その全部について
の確率に応じて積分しよう
の確率密度分布を[tex:G(k+a,L+b) = \frac{\lambda^{(k+a)-1}exp(-(L+b)\lambda)}{\Gamma*1(\frac{1}{(L+b)})^k}]と推定することにする
のポアソン分布でN回の観察をすれば、
回の生起が期待されるから、t回生起する確率は
について積分すればよいから
が知りたい確率
について考える
であることから、



