フローサイトメータデータの解析
- nature_biotechnology論文
- bioconductorサイト
- cytoSPADEのステップ
- 1. Density-dependent down-sampling
library(vegan) library(GPArotation) library(igraph) library(rgl) library(MCMCpack) # データの座標によらず、視野内に収めるための補正 vision.scale <- function(x,scl){ (x-min(x))/(max(x)-min(x)) * scl + (1-scl)/2 } # 観察対象をきちんと視野内に収めるために、周辺部にはシグナルがないように調整する vision.standard <- function(x,scl = 0.9){ rg <- apply(x,2,range) tmp <- apply(x,2,vision.scale, scl) return(list(st.x = tmp,rg=rg)) } # 視野全体のピクセル数を指定して、該当する超立方体の番地にする round.coords <- function(x,n.cell=50){ d <- length(x[1,]) matrix(floor(x * n.cell),ncol=d) } library(vegan) library(GPArotation) library(igraph) library(rgl) library(MCMCpack) # d:次元 # n.steps:枝分かれ回数 # n.pt.raneg:小集団の点の数 # NN:数を増やすスケール # min.v,max.v:枝の長さの上下限 # できた木の上の点に誤差項を入れるときの係数 my.FACS.pts <- function(d,n.steps=10,n.pt.range=100:1000,NN=100,min.v=5,max.v=10,v=0.3){ # 点の座標 X <- matrix(0,0,d) # 枝分かれを繰り返す # ステップごとの点の数 tmp.ns <- sample(n.pt.range,n.steps,replace=TRUE) # ステップごとの小集団の広がり(半径)を決める係数 tmp.Ls <- runif(n.steps,min.v,max.v) for(i in 1:n.steps){ tmp.n <- tmp.ns[i] tmp.X <- matrix(0,tmp.n,d) tmp.L <- tmp.Ls[i] # 基準点からの距離の２乗に応じて確率が下がるような生起確率を作り tmp.V <- seq(from=0,to=1,length=tmp.n*NN) tmp.prob <- (tmp.V-mean(tmp.V))^2 tmp.prob <- tmp.prob/sum(tmp.prob) # それに応じてtmp.n個の点を発生させる tmp.S <- tmp.V[sort(sample(1:length(tmp.V),tmp.n,replace=TRUE,prob=tmp.prob))]*tmp.L # 枝上の位置を算出したので、それを適当な方向に回転する tmp.X[,1] <- tmp.S tmp.R <- Random.Start(d) tmp.X <- tmp.X %*% tmp.R # 枝は既存の位置から生やす if(i > 1){ # 既存の位置から１点を選ぶ tmp.st <- sample(1:length(X[,1]),1) #tmp.st.2 <- sample(1:tmp.n,1) # 新しい枝は始点から「生える」だけにする tmp.st.2 <- 1 st.pt <- X[tmp.st,] connect.pt <- tmp.X[tmp.st.2,] # 生え際を基準に座標を取り直す tmp.X <- t(t(tmp.X) + st.pt - connect.pt) } # 新枝の点を加える X <- rbind(X,tmp.X) } # X <- X + rnorm(length(X),0,v) X.curve <- X for(i in 1:d){ X.curve[,i] <- sign(X.curve[,i]) * abs(X.curve[,i]^2) } X <- X.curve return(X) } # 適当に線状の点の集まりを作る d <- 3 n.steps <- 10 n.pt.range <- 100:1000 NN <- 100 my.X <- my.FACS.pts(d,n.steps,n.pt.range,NN) plot(as.data.frame(my.X)) # データの座標によらず、視野内に収めるための補正 vision.scale <- function(x,scl){ (x-min(x))/(max(x)-min(x)) * scl + (1-scl)/2 } # 観察対象をきちんと視野内に収めるために、周辺部にはシグナルがないように調整する vision.standard <- function(x,scl = 0.9){ rg <- apply(x,2,range) tmp <- apply(x,2,vision.scale, scl) return(list(st.x = tmp,rg=rg)) } # 視野全体のピクセル数を指定して、該当する超立方体の番地にする round.coords <- function(x,n.cell=50){ d <- length(x[1,]) matrix(floor(x * n.cell),ncol=d) } # 適当に線状の点の集まりを作る d <- 3 n.steps <- 10 n.pt.range <- 100:1000 NN <- 100 my.X <- my.FACS.pts(d,n.steps,n.pt.range,NN) plot(as.data.frame(my.X)) 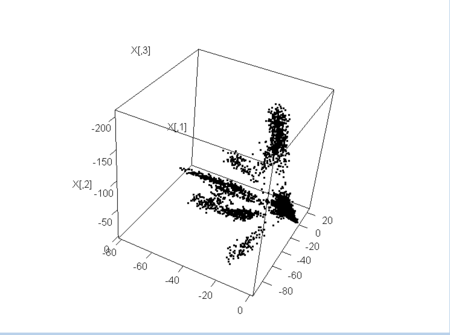plot3d(my.X[,1:3])
-
-
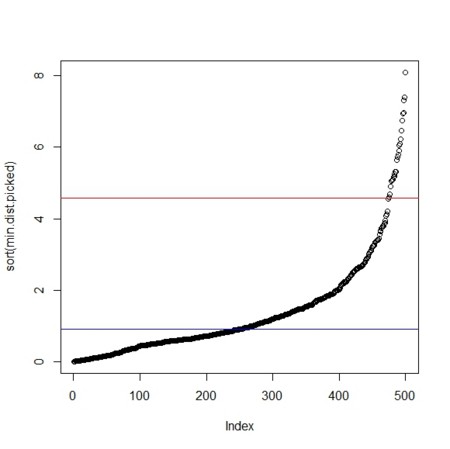
- 点をサンプリングして最近点距離分布をとる(ソートしてプロット)。その中央値と中央値のα=5倍を示しておく
-
# No. points n <- length(X[,1]) print(n) # あまり多くなくやっておこう # n.pick個の点について最近点距離を求める n.pick <- 500 # 2000ではなく少なめでやってみる picked <- sample(1:n,n.pick) min.dist.picked <- rep(0,n.pick) for(i in 1:n.pick){ tmp <- t(X)-X[picked[i],] tmp2 <- apply(abs(tmp),2,sum) tmp2[which(tmp2==0)] <- max(tmp2)+1 min.dist.picked[i] <- min(tmp2) } plot(sort(min.dist.picked)) mdan <- median(min.dist.picked) abline(h=mdan,col=4) alpha <- 5 L <- mdan*alpha abline(h=L,col=2)
-
-
- 近傍定義の基準距離に照らして局所濃度を算出する
-
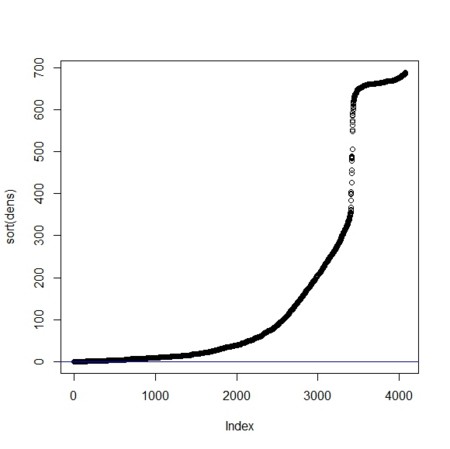
dens <- rep(0,n) for(i in 1:n){ tmp <- t(X)-X[i,] tmp2 <- apply(abs(tmp),2,sum) tmp2[which(tmp2==0)] <- max(tmp2)+1 dens[i] <- length(which(tmp2<=L)) } OD.perc <- 0.01 # 論文では0.01 TD.perc <- 0.03 # 論文では0.03 OD.TD <- quantile(dens,c(OD.perc,TD.perc)) plot(sort(dens)) abline(h=OD.TD[1],col=2) abline(h=OD.TD[2],col=4)
-
-
- ダウンサンプリングする(下がオリジナル)
-
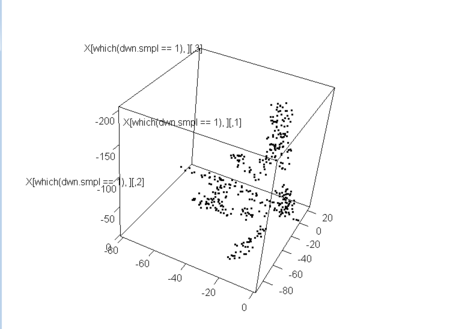
dwn.smpl <- rep(0,n) for(i in 1:n){ if(dens[i] <=OD.TD[1]){ }else if(dens[i] <= OD.TD[2]){ dwn.smpl[i] <- 1 }else{ if(OD.TD[2]==0){ tmp.prob <- 1/dens[i] }else{ tmp.prob <- OD.TD[2]/dens[i] } dwn.smpl[i] <- sample(0:1,1,prob=c(1-tmp.prob,tmp.prob)) } } sum(dwn.smpl)/n # ダウンサンプリング率 X.dwn <- X[which(dwn.smpl==1),] plot3d(X.dwn)
- 2. クラスターに分ける
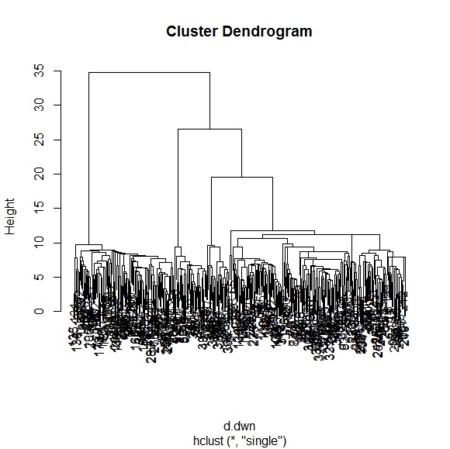
# single linkage method はhclust()のmethod="single" d.dwn <- dist(X.dwn,method="manhattan") cl <- hclust(d.dwn,method="single") num.cl <- 5 cl2 <- cutree(cl, k=num.cl)
cl.coords <- matrix(0,num.cl,length(X.dwn[1,])) for(i in 1:num.cl){ tmp <- X.dwn[which(cl2==i),] if(is.matrix(tmp)){ cl.coords[i,] <- apply(tmp,2,median) }else{ cl.coords[i,] <- tmp } }
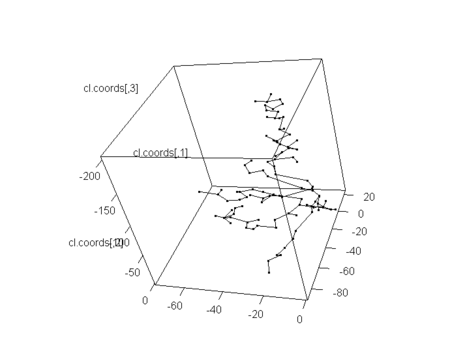
library(nnclust) a<-mst(cl.coords) plot(cl.coords[,1:2]) segments(cl.coords[a$from,1], cl.coords[a$from,2], cl.coords[a$to,1], cl.coords[a$to,2],col="blue") plot3d(cl.coords) for(i in 1:length(a$from)){ seg.m <- matrix(c(cl.coords[a$from[i],1],cl.coords[a$from[i],2],cl.coords[a$from[i],3],cl.coords[a$to[i],1],cl.coords[a$to[i],2],cl.coords[a$to[i],3]),byrow=TRUE,nrow=2) segments3d(seg.m) }
- 4 全細胞を木構造につなげるべくup-samplingする
n.members <- rep(0,num.cl) for(i in 1:n){ tmp <- t(X.dwn)-X[i,] tmp2 <- apply(abs(tmp),2,sum) #tmp2[which(tmp2==0)] <- max(tmp2)+1 tmp3 <- which(tmp2==min(tmp2))[1] tmp4 <- cl2[tmp3] n.members[tmp4] <- n.members[tmp4] + 1 } plot3d(cl.coords) for(i in 1:length(a$from)){ seg.m <- matrix(c(cl.coords[a$from[i],1],cl.coords[a$from[i],2],cl.coords[a$from[i],3],cl.coords[a$to[i],1],cl.coords[a$to[i],2],cl.coords[a$to[i],3]),byrow=TRUE,nrow=2) segments3d(seg.m) } max.r <- max(cl.coords)-min(cl.coords) for(i in 1:num.cl){ spheres3d(cl.coords[i,],radius=(n.members[i]/max(n.members))^(1/length(X[1,]))*max.r/20) }
