2014-02-01

臨床マーカーの値の分布〜下限のある値の分布

多くの量的臨床マーカーは、下限値を持つ。下限値を持たないものを挙げることが難しいくらい
たくさんの標本で観察すると、正規分布に似ることが多いが、正規分布は下限値がない
また、生命現象では、対数正規分布になりがちであることも経験的に(理論もあるかも…)知られているので、臨床マーカーの分布として対数正規分布を使うこともあるし、観察値の対数を取って、正規分布とみなして解析することもある
今日は、下限値のある３つの分布の様子を眺める
３つの分布は、対数正規分布、ワイブル分布、フレシェ分布である。このうちワイブル分布とフレシェ分布は極値分布として同じ仲間として扱われることもある
まず、対数正規分布は、台が0以上であって、累積分布が次のようになる関数
- ２つのパラメタ、m,sがあって、累積分布がsによらず、 $(e^m,0.5)$ を通るような関数
- 台が0以上、無限大までなので、分布は小さい方は0の方で断ち切れ、大きい方は無限に裾を引くような右裾広がりな分布となる

x <- seq(from=0,to=10,length=100)
x <- x[-1]
s <- seq(from=0,to=10,length=20)
s <- s[-1]
m <- 1:5
P.lgnrm <- list()

for(j in 1:length(m)){
	tmp <- matrix(0,length(s),length(x))
for(i in 1:length(s)){
	tmp[i,] <- plnorm(x,log(m[j]),log(s[i]))
}
P.lgnrm[[j]] <- tmp
}
plot(x,x,xlim=c(0,max(x)),ylim=c(0,1),col=0)
for(i in 1:length(m)){
	for(j in 1:length(s)){
		points(x,P.lgnrm[[i]][j,],type="l",col=j)
	}
	
}

次にワイブル分布。この分布は、時間とともに故障率が変化する(故障しやすくなったり、故障しにくくなったり)ときの、寿命の分布として知られる。臨床的異常が「故障」であると考えるとこれも臨床マーカーと関係する理由付けは得られる
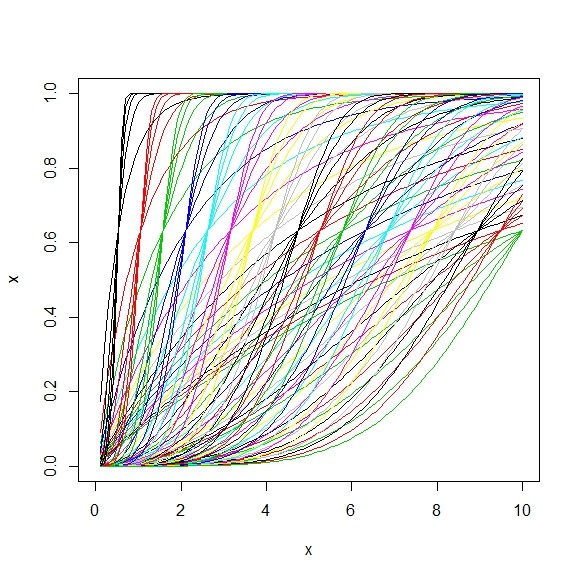
このワイブル分布も累積分布をみると２個のパラメタのうちの1つmにのみ依存した $(k,1-e)$ という定点をsに寄らずに通る
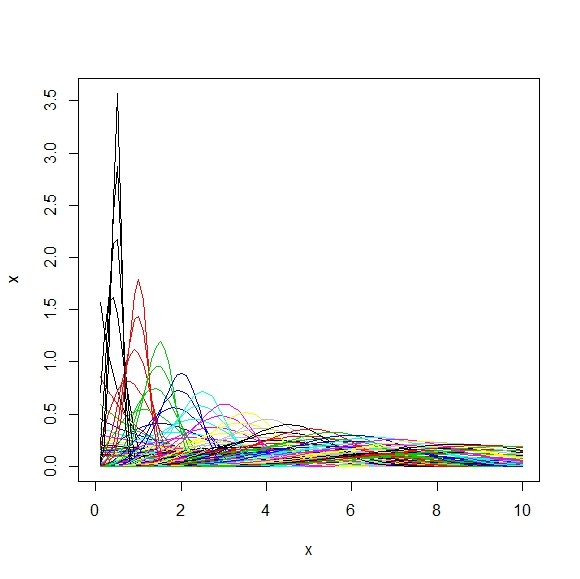
この累積分布が定点を通るという性質は先の対数正規分布と同じだが、確率密度分布は左に裾を引いており、右に移るにつれて正規分布に近くなる様子がわかる

x <- seq(from=0,to=10,length=100)
x <- x[-1]
s <- seq(from=0,to=10,length=20)
s <- s[-1]
m <- 1:5
D.lgnrm <- list()
P.lgnrm <- list()

for(j in 1:length(m)){
	tmp <- tmp2 <- matrix(0,length(s),length(x))
for(i in 1:length(s)){
	tmp[i,] <- pweibull(x,m[j],(s[i]))
	tmp2[i,] <- dweibull(x,m[j],(s[i]))
}
P.lgnrm[[j]] <- tmp
D.lgnrm[[j]] <- tmp2
}
plot(x,x,xlim=c(0,max(x)),ylim=c(0,1),col=0)
for(i in 1:length(m)){
	for(j in 1:length(s)){
		points(x,P.lgnrm[[i]][j,],type="l",col=j)
	}
	
}
plot(x,x,xlim=c(0,max(x)),ylim=c(0,max(unlist(D.lgnrm))),col=0)
for(i in 1:length(m)){
	for(j in 1:length(s)){
		points(x,D.lgnrm[[i]][j,],type="l",col=j)
	}
	
}

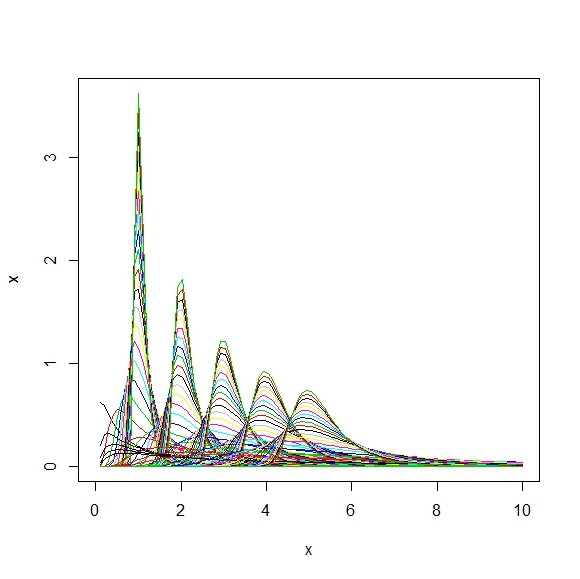
次のフレシェ分布も累積分布に、２つのパラメタのうち１つにのみ依存する定点がある
フレシェ分布は(も)３パラメタの確率分布であるが、下限値が0であるような分布はそのうちの1つのパラメタの値が0で固定されるので、実質的に2パラメタある
定点は(s,1/e)である
裾を引くのは右方向

x <- seq(from=0,to=10,length=100)
x <- x[-1]
s <- seq(from=0,to=10,length=20)
s <- s[-1]
m <- 1:5
D.lgnrm <- list()
P.lgnrm <- list()

for(j in 1:length(m)){
	tmp <- tmp2 <- matrix(0,length(s),length(x))
for(i in 1:length(s)){
	tmp[i,] <- pfrechet(x,0,m[j],(s[i]))
	tmp2[i,] <- dfrechet(x,0,m[j],(s[i]))
}
P.lgnrm[[j]] <- tmp
D.lgnrm[[j]] <- tmp2
}
plot(x,x,xlim=c(0,max(x)),ylim=c(0,1),col=0)
for(i in 1:length(m)){
	for(j in 1:length(s)){
		points(x,P.lgnrm[[i]][j,],type="l",col=j)
	}
	
}
plot(x,x,xlim=c(0,max(x)),ylim=c(0,max(unlist(D.lgnrm))),col=0)
for(i in 1:length(m)){
	for(j in 1:length(s)){
		points(x,D.lgnrm[[i]][j,],type="l",col=j)
	}
	
}