イベント集積に関するメモ

n <- 1000
# ランダムに脱落する
prob <- c(0.5,0.5)
censor <- sample(0:1,n,replace=TRUE,prob=prob)
# 指数乱数で死亡時刻が決まる
#times <- cumsum(rexp(n))
times <- sort(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
#par(mfcol = c(1,2))
#plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)

# 簡単のため２群の人数は同じにします
n1 <- 1000
n2 <- 1000
# 第１群のイベント発生率に対して、第２群のイベント発生率を１倍から２倍まで振ります
p1 <- 1
p2s <- seq(from=1,to=2,length=9)

# 第２群のイベント発生率ごとにn.iter回、スタディが実施されたとします
# 脱落はなしとします
n.iter <- 1000

# 第１群のイベント累積発生が5%のときと10%のときとで２群の累積発生率が入れ替わるかどうかを勘定します。その記録用の行列です
cross <- matrix(0,length(p2s),n.iter)
# 全シミュレーションの結果格納リスト
res <- list()
# 第２群の発生率でループ
for(j in 1:length(p2s)){
	p2 <- p2s[j]
	res[[j]] <- array(0,c(n.iter,n1+1,2))
	# n.iter回の繰り返し
	for(i in 1:n.iter){
		# イベントが一定確率で起きるポアソン事象と仮定すれば
		# イベント間隔は指数分布に従うので、指数乱数を使ってイベント時刻を定めます
		# x1 <- sort(rexp(n1,p1))のように各個人にポアソンイベントが１回だけ発生すると考えて、発生時刻をシミュレーションするのもありです。どちらでやっても、この段階では、直線的に累積して行きます
		x1 <- cumsum(rexp(n1,p1))
		x2 <- cumsum(rexp(n2,p2))
		# 時刻0にはイベントは0
		res[[j]][i,,1] <- c(0,x1)
		res[[j]][i,,2] <- c(0,x2)
		# 第１群の5パーセンタイル、10パーセンタイル時刻
		time1 <- quantile(x1,0.05)
		time2 <- quantile(x1,0.1)
		# ２つの時刻での第１、第２群でのイベント発生率
		x1.1 <- length(which(x1>time1))/n1
		x1.2 <- length(which(x1>time2))/n1
		x2.1 <- length(which(x2>time1))/n2
		x2.2 <- length(which(x2>time2))/n2
		# ２時刻でのイベント発生率の逆転を判定
		if((x1.1-x2.1)*(x1.2-x2.2)<0){
			cross[j,i] <- 1
		}

	}
}
# 逆転率を第２群の発生率別に計算
num.frac <- apply(cross,1,sum)/n.iter

# n.iter試行のうち10回分について累積状況をプロット
# 併せて、逆転率を記載します
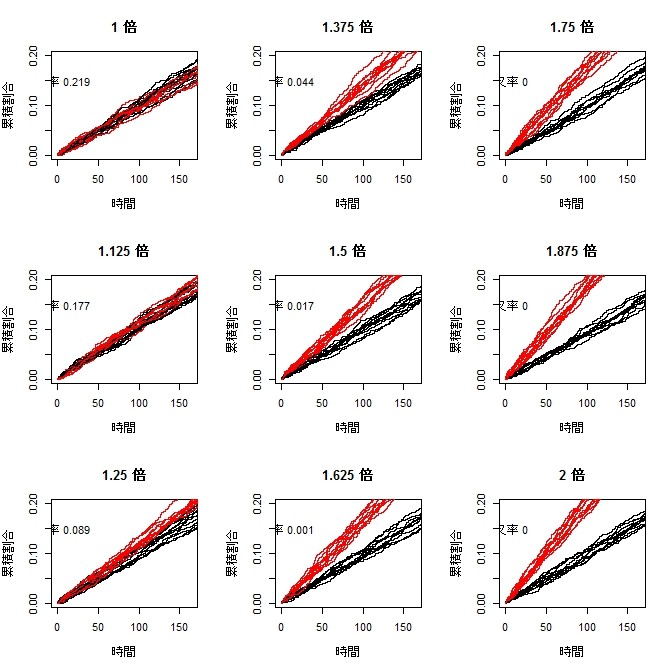
par(mfcol=c(3,3))

for(j in 1:length(p2s)){
	plot(res[[j]][1,,1],(0:n1)/n1,type="s",xlim=c(0,quantile(x1,0.15)),ylim=c(0,0.2),xlab="時間",ylab="累積割合",main=paste(p2s[j]/p1,"倍"))
	points(res[[j]][1,,2],(0:n2)/n2,type="s",col=2)
	for(i in 2:10){
		points(res[[j]][i,,1],(0:n1)/n1,type="s")
		points(res[[j]][i,,2],(0:n2)/n2,type="s",col=2)
	}
	text(0.05,0.15,paste("交叉率",num.frac[j]))
}

par(mfcol=c(1,1))


#d1 <- data.frame(Censor = cens1, Time = x1)
#d2 <- data.frame(Censor = cens2, Time = x2)

Data <- data.frame(Censor = c(cens1,cens2), Time = c(x1,x2), Drug = c(rep(1,n1),rep(2,n2)))

surv.out <- survfit(Surv(Data$Time,Data$Censor)~strata(Data$Drug))
plot(surv.out)