2014-05-01

次に何が出る？　ディリクレ、色々お試し編

一昨日・昨日と、カテゴリ数が未知のときのディリクレ分布の合算の話をしてきた(
- まだ、この方法でＯＫ、という確信はないのだが、まあ、これまでのところ、出てくる値もそれなりに妥当そうなので、このまま行ってみる(一番、危なそうなのは、事前確率をすべてのカテゴリ数に関して均等割りにしているところ、とか…)
- 次に出るのが既出のカテゴリなのか、未出カテゴリなのかを含めて予想しようという話
- 少し条件を制約するなりして、その挙動を見てみることにする
場合１：たった１つのカテゴリしか観測されないが、その観測数がだんだん増える場合
- その観測数が増えるにつれ、新たなカテゴリが出てくる可能性は減ってきて、どうせ次も同じだろうと思うわけだが、その様子
- 昨日の関数の再掲になるが、今日の記事の中で完結するように、再度。

my.beta <- function(a){
	exp(sum(lgamma(a))-lgamma(sum(a)))
}
#[tex:\frac{(\sum a_i)!}{\prod a_i!}]
my.comb <- function(a){
	exp(lgamma(sum(a)+1)-sum(lgamma(a+1)))
}
#[tex:C(\mathbf{a})\frac{B(2\mathbf{a}-1)}{B(\mathbf{a}}]
my.CBB <- function(a){
	my.like.dir(a)*exp(lgamma(sum(a)-length(a)+1)-sum(lgamma(a)))
}
#組合せ項は比を取る時は不要なので取り除いたもの
my.like.dir <- function(a){
	my.beta(2*a-1)/my.beta(a)
}
# 観測度数bを使って比を上記の比を計算
my.like.dir.obs <- function(b){
	if(length(b)==1){
		return(1)
	}
	a <- b+1
	my.like.dir(a)
}
# サンプル数n、観察カテゴリ数k、想定カテゴリ数Kの場合のk, K 頂点正単体空間の発生確率総積分
my.ratio.dir.integral <- function(n,k,K){
	exp(lgamma(n+K)-lgamma(2*n+K)-lgamma(n+k)+lgamma(2*n+k))
}
# この比を出す代わりに、相対値をベクトルで…
my.relative.dir.integral <- function(n,K){
	exp(lgamma(n+K)-lgamma(2*n+K))
}
# k種類観測されたときにK種類を想定した場合の期待値
# aは観測度数に1を加えたベクトル
my.expected.dirichlet <- function(a,K){
	b <- c(a,rep(1,K-length(a)))
	b/sum(b)
}
# vは観測回数のベクトル
my.expected.dirichlet.obs <- function(v,K){
	a <- v+1
	my.expected.dirichlet(a,K)
}
my.ratio.dir.integral(n=4,k=3,K=4)

c(my.expected.dirichlet.obs(c(2,1,1),3),0)
my.expected.dirichlet.obs(c(2,1,1),4)

my.relative.dir.integral(4,c(3,4))

# v を観測したときにk=length(v)から、k,k+1,....とやる関数
# 最大Kと事前確率ベクトルはデフォルト値を与える
my.exp.dirichlet.multi <- function(v,maxK=length(v)+1000,pre=rep(1/(maxK-length(v)+1),maxK-length(v)+1)){
	# vは観測回数ベクトル。0より大の値
	k <- length(v)
	K <- k:maxK
	# 総観測数
	n <- sum(v)
	# 仮説の事後確率
	pr <- my.relative.dir.integral(n,K)
	pr. <- pr/sum(pr)
	pr.. <- pre * pr.
	pr.. <- pr../(sum(pr..))
	# 仮説別期待値
	pkK <- matrix(0,length(K),maxK)
	for(i in 1:length(K)){
		pkK[i,1:K[i]] <- my.expected.dirichlet.obs(v,K[i])
	}
	tmp <- pkK * pr..
	expected.prob <- apply(tmp,2,sum)
	unobs <- sum(expected.prob[(k+1):maxK])
	expected.prob.obs.unobs <- c(expected.prob[1:k],unobs)
	return(list(v=v,n=n,k=k,maxK=maxK,K=K,pre=pre,post=pr..,pkK=pkK,pr.matrix=tmp,expected.prob=expected.prob,expected.prob.obs.unobs=expected.prob.obs.unobs))
}

- まずは、たった１度の試行で、あるカテゴリが観察されたとき、次に同じカテゴリを期待するか、違うカテゴリを期待するか

v <- c(1)
tmp.out <- my.exp.dirichlet.multi(v,maxK=1001)
# 既出か未出か
tmp.out$expected.prob.obs.unobs

> tmp.out$expected.prob.obs.unobs
[1] 0.1985171 0.8014829

- - これをmaxK=100とすると、0.3026161 0.6973839、maxK=10000とすると、0.1467582 0.8532418、となる
  - maxKに応じて、既出の確率が下がっていく。K=無限になると0になるのだろう
  - たった1観測では、次に同じものが出るか違うものが出るかは、いったい、カテゴリ数はどこまで増え得るのか、という事前予想に依存していることがわかる。
  - 実際問題、どう感じるか…、と自分の頭に問うと、「同じのが出るわけがないと思ったかと思うと、いやいや、同じものが出るかも」と思い返したりして、「同じものが出る確率の期待値」があるというよりは、量子雲があって決まらない、という感じがする
- では、１カテゴリが10回連続観察されたとすると、最大カテゴリ数予想とともにどのような変化をするだろうか
  - 少しずつ、既出カテゴリの期待値が下がるが、それほど下がらないので、「現実的な予想の範囲内では有限、かつかなりの高確率」を期待できる、と読める

> tmp.out <- my.exp.dirichlet.multi(v,maxK=11)
> tmp.out$expected.prob.obs.unobs
[1] 0.9099606 0.0900394
> tmp.out <- my.exp.dirichlet.multi(v,maxK=101)
> tmp.out$expected.prob.obs.unobs
[1] 0.9070024 0.0929976
> tmp.out <- my.exp.dirichlet.multi(v,maxK=1001)
> tmp.out$expected.prob.obs.unobs
[1] 0.90700239 0.09299761
> tmp.out <- my.exp.dirichlet.multi(v,maxK=10001)
> tmp.out$expected.prob.obs.unobs
[1] 0.90700239 0.09299761

- １カテゴリだけが観測されることが繰り返されたとき、どんな具合で未観測カテゴリの出現が期待できるだろうか。これまでに見たように、最大カテゴリ数に有限値を設定すると、無限値の場合と異なることがわかっているので、この推定は有限であること、特に観測回数が少ないときには、有限と現の差が大きいことに注意して解釈することにする。以下はK=k+1000=1001の場合

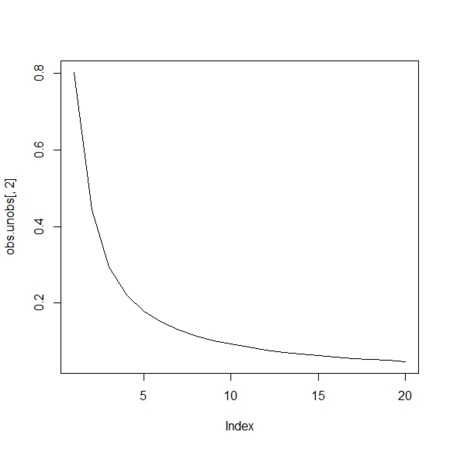
single.obs <- 1:20
obs.unobs <- matrix(0,length(single.obs),2)
for(i in 1:length(single.obs)){
	tmp.out <- my.exp.dirichlet.multi(c(single.obs[i]),maxK=1001)
	obs.unobs[i,] <- tmp.out$expected.prob.obs.unobs
}

plot(obs.unobs[,2],type="l")

- 今度は次から次へと新たなカテゴリばかりが続くときに、次も新たなカテゴリだと期待するのはどれくらいの確率になるかを見てみる。ここでも、最大カテゴリ数が無限だと、「いつも次は新しいカテゴリ」を期待するのが適当になる？？ので、以下の結果は「有限なカテゴリ数」での話
  - n回観測して、n回とも異なるカテゴリの場合には、「次も新しいカテゴリ」を期待する確率は $\frac{1}{n}$ (くらい)らしい

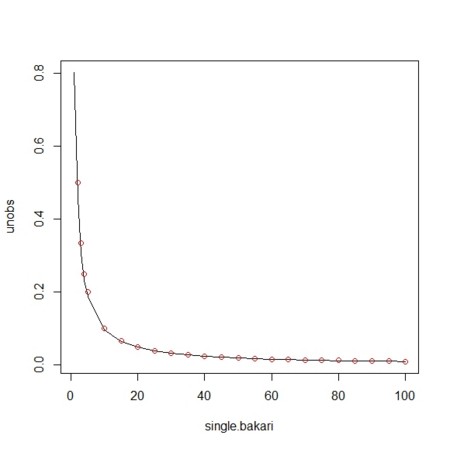
single.bakari <- c(1:4,(1:20)*5)
unobs <- rep(0,length(single.bakari))
for(i in 1:length(single.bakari)){
	tmp.out <- my.exp.dirichlet.multi(rep(1,single.bakari[i]))
	unobs[i] <- tmp.out$expected.prob.obs.unobs[single.bakari[i]+1]
}

plot(single.bakari,unobs,type="l")
points(single.bakari,1/single.bakari,col=2)

- 何か適当な観測回数でやってみよう。実観測割合を赤でプロット。黒は未観測カテゴリもあるものとしての予測確率。未観測カテゴリはたくさんあるが1つにまとめる

# 適当にポアソン分布乱数、テーブル化したりして、適当なvを作る
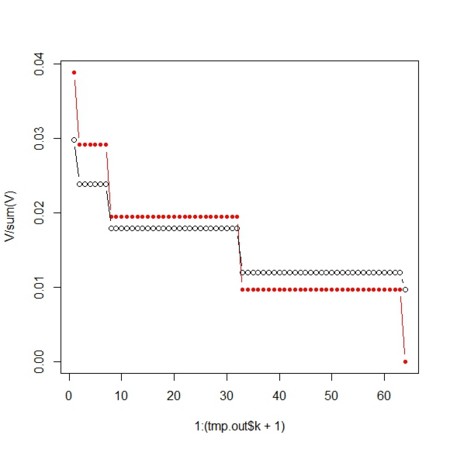
tmp <- rpois(100,0.9)
b <- table(tmp)
b
b <- b[-1]
b
v <- c()
for(i in 1:length(b)){
	v <- c(v,rep(i,b[i]))
}
v <- sort(v,decreasing=TRUE)
tmp.out <- my.exp.dirichlet.multi(v)
# 未観測プールカテゴリを入れる
V <- c(v,0)
plot(1:(tmp.out$k+1),V/sum(V),col=2,pch=20,type="b")
points(1:(tmp.out$k+1),tmp.out$expected.prob.obs.unobs,type="b")