直線の傾きの乱雑さ

• 昨日の記事で、ルールのある軌道に観察乱雑項が入ったときは、微小区間では方向変化が一様分布するが、長区間では一様(乱雑)が見えなくなることを書いた
• 今日の記事は、そのもっとも単純な例、「定速進行」＋「観察乱雑項」の場合に方向変化は観察点間距離とどのような関係になるのかの分布をとってみる話
• これがわかれば、どうやって「観察乱雑項」を排除するかの目安がわかる
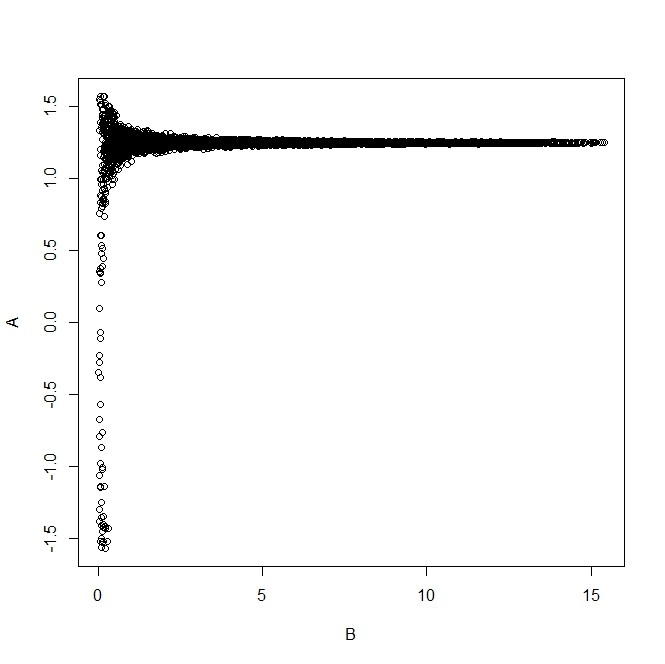
• 距離が無限小では一様分布、長くなると収束する様子がわかる

t <- sort(runif(100)*5)
x <- t
y <- x * 3
y. <- y + rnorm(length(y),0,0.1)

#x <- cos(t)
#y <- sin(t)
#y. <- y+ rnorm(length(y),0,0.1)

plot(x,y.,pch=20)
abline(0,3,col=2)

A <- B <- c()
for(i in 1:(length(x)-1)){
	for(j in (i+1):length(x)){
		tmp <- (y.[j]-y.[i])/(x[j]-x[i])
		tmp.v <- c(x[j]-x[i],y.[j]-y.[i])
		A <- c(A,atan(tmp))
		B <- c(B,sqrt(sum(tmp.v^2)))
	}
}
hist(A)

plot(B,A)