- こちらの記事で、関数解析について勉強した
- 2次元に時刻パラメタで記録された曲線の解析をしてみよう
- テキストブックのサンプルコードはこちら
- データはこんな感じ
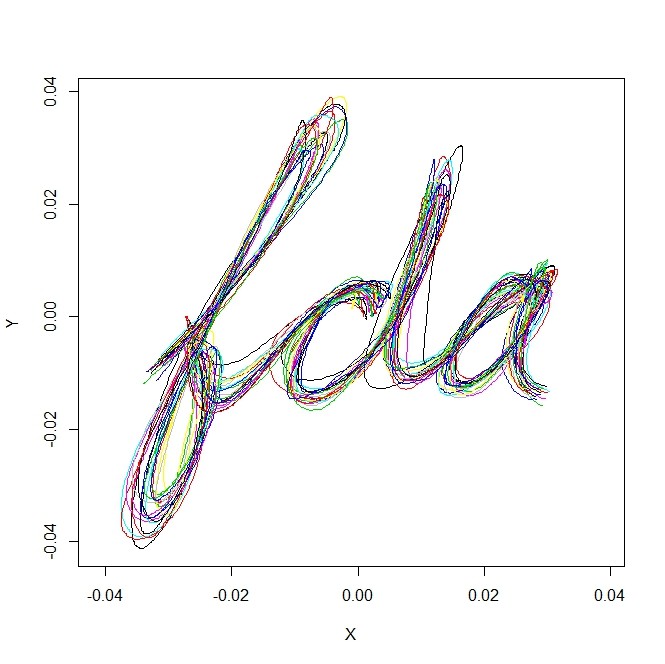
library(fda)
dim(handwrit)
plot(handwrit[,1,],type="l",xlim=range(handwrit),ylim=range(handwrit))
for(i in 2:20){
points(handwrit[,i,],type="l",col=i)
}
- 単純に20本のカーブの「平均カーブ」を作って描いてみる
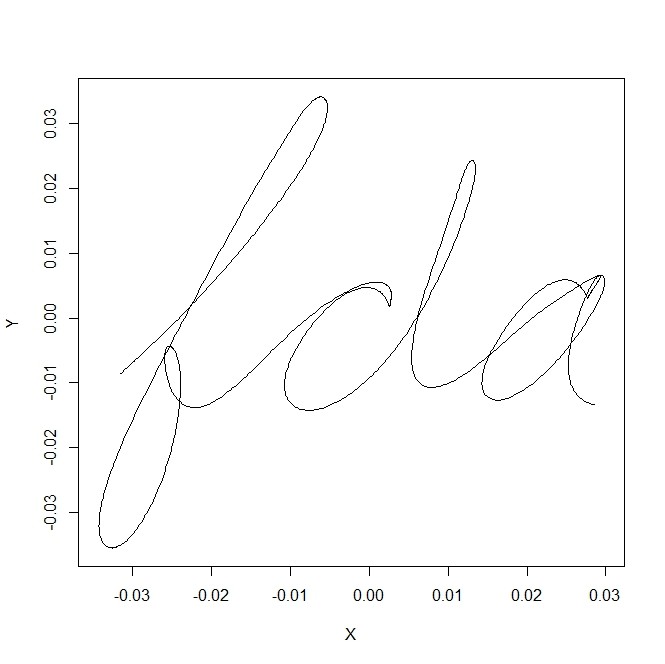
simple.mean <- apply(handwrit,c(1,3),mean)
plot(simple.mean,type="l")
- 20本のカーブの特徴(癖)を取り出す
- 手順としては、適当に関数の線形和に分解し、それを分散に着目して、成分の大きい方から取り出してやる
- すべての分散軸を取り出せば元通りの曲線を表すが、寄与度の低い分を捨てれば、次元を落とせる
- まずは、基底関数を少なくしてやってみる(全部の情報は取り出せない)(赤は単純な20本の平均、黒が、平滑化した上での平均、情報が少なすぎて、超いい加減なサインみたいに見えます)
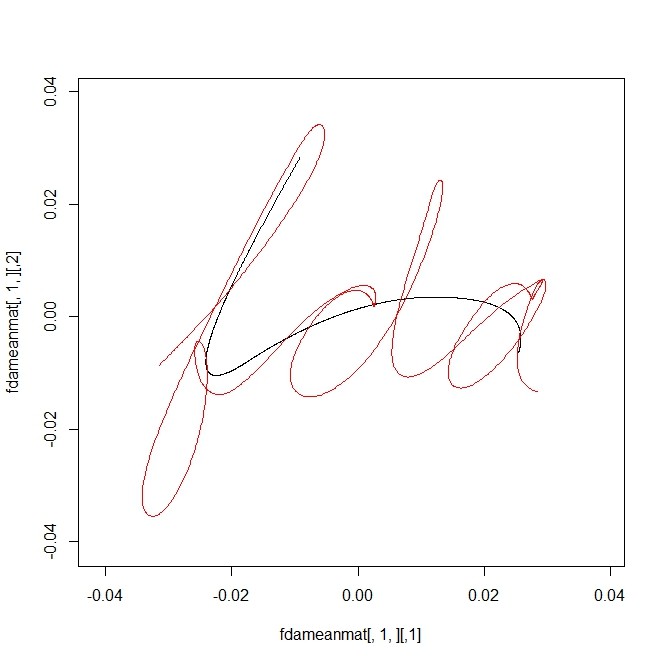
fdatime <- seq(0,1,len=dim(handwrit)[1])
fdarange <- c(0,1)
fdabasis <- create.bspline.basis(fdarange,4,3)
fdafd <- smooth.basis(fdatime,handwrit,fdabasis)$fd
fdameanfd = mean(fdafd)
fdameanmat = eval.fd(fdatime, fdameanfd)
plot(fdameanmat[,1,],type="l",xlim=range(handwrit),ylim=range(handwrit))
points(simple.mean,type="l",col=2)
-
- じゃあ、関数はいくつにすればよいかを考えてみる。階数(?)は関数の数を上限とするのでひとまず3から200でやってみる
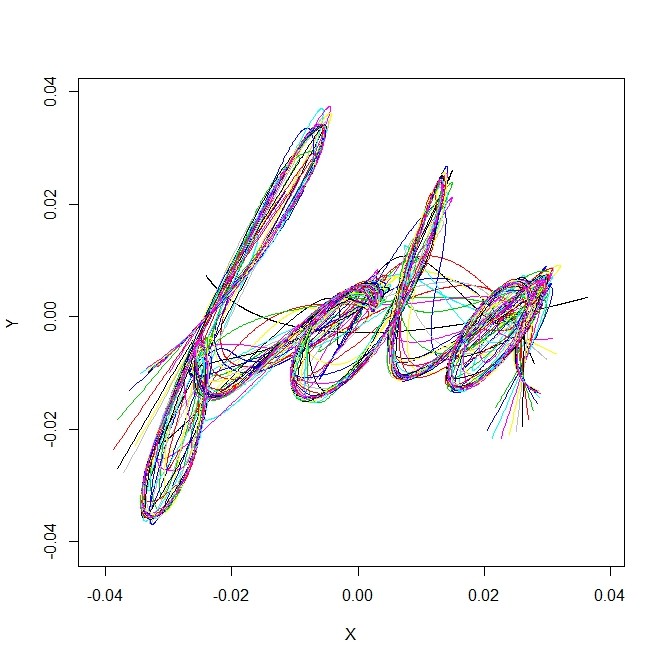
plot(simple.mean,type="l",xlim=range(handwrit),ylim=range(handwrit))
n.f <- 3:200
diff.from.simple.mean <- rep(0,length(n.f))
for(i in 1:length(n.f)){
fdabasis <- create.bspline.basis(fdarange,n.f[i],3)
fdatime <- seq(0,1,len=dim(handwrit)[1])
fdafd <- smooth.basis(fdatime,handwrit,fdabasis)$fd
fdameanfd = mean(fdafd)
fdameanmat = eval.fd(fdatime, fdameanfd)
points(fdameanmat[,1,],type="l",col=i)
diff.from.simple.mean[i] <- sum((fdameanmat[,1,]-simple.mean)^2)
}
-
- 単純な平均との残差平方和がだんだん0になっていくことを図で示す
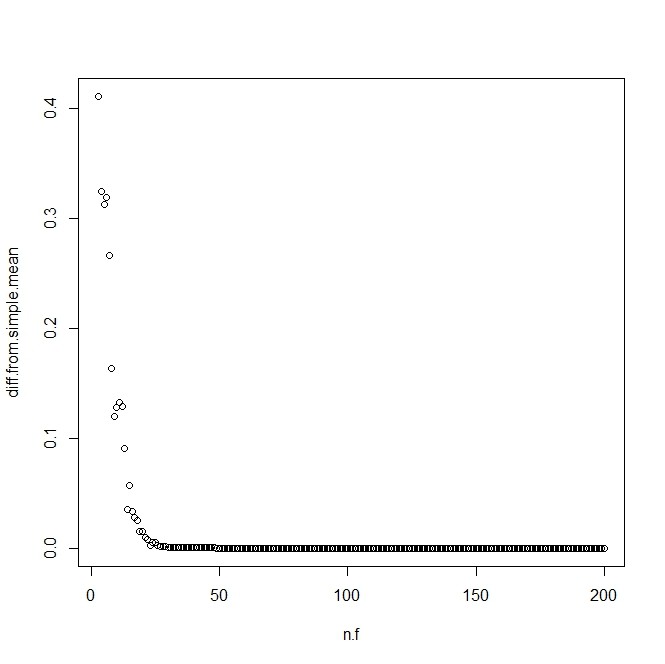
plot(n.f,diff.from.simple.mean)
-
- どうやって、基底の数を選んだり、階数(?)を決めたりすればよいか…。いろいろやってみて、なるべく少ない基底と階数で、「シンプル平均」とそこそこ近いのを選べばよいか…
- 今はその決め方はスキップして、テキストブックが選んだ、105,6を使ってみる。一致しすぎて、重ねてプロットしていることがわからないくらいです
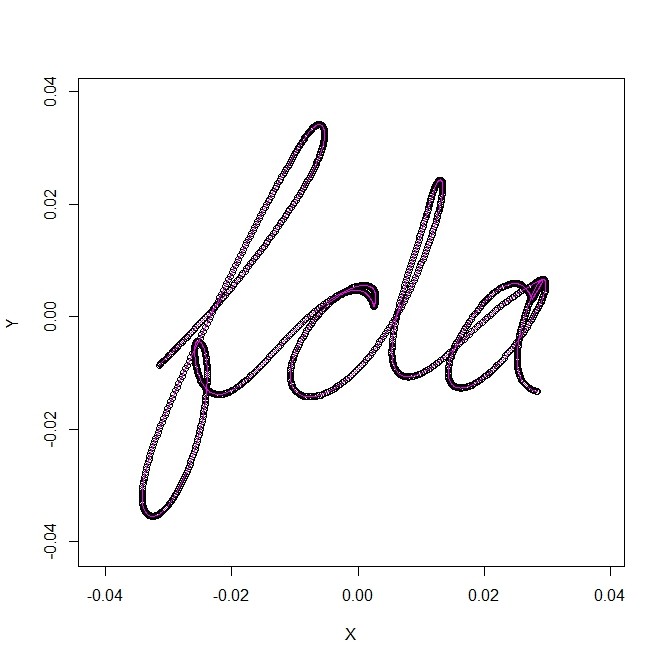
fdabasis <- create.bspline.basis(fdarange,105,6)
fdatime <- seq(0,1,len=dim(handwrit)[1])
fdafd <- smooth.basis(fdatime,handwrit,fdabasis)$fd
fdameanfd = mean(fdafd)
fdameanmat = eval.fd(fdatime, fdameanfd)
plot(simple.mean,type="b",xlim=range(handwrit),ylim=range(handwrit))
points(fdameanmat[,1,],type="l",col=i)
-
- 次に、どのくらいのトップ関数を採用するべきかを判断するために、"PCA"のeigenvaluesを計算する。
- 採用数を仮に5とする(この値に何を与えても、eigenvaluesは結局全部出るので、ここではnharmの値は適当でよい
- 念のため異なるnharmの値でeigenvaluesを出して、等しいことを確認しておく
nharm <- 5
fdapcaList <- pca.fd(fdafd,nharm)
fdaeig <- fdapcaList$values
nharm2 <- 50
fdapcaList2 <- pca.fd(fdafd,nharm2)
fdaeig2 <- fdapcaList2$values
plot(fdaeig,fdaeig2)
-
- 意味のある成分数を選ぶ
- あからさまに意味のある・ないで分けることができる。さらに、意味のある19成分を、対数スケールで直線に載るか、それよりもさらに上に上がるかで見ると、上位3個は、残りの16個が作る直線の上に来るので、特に異議が強い(と本では述べて)、上位3つを選んでいた。19ではだめなのか(増やしたところで、増やしたほどの改善がない、ということなのだろう)とは思うが、ここもテキストブックの通り3つをとっておこう
- この19と言う数字は、サンプル数(筆記カーブ数)から1引いたもの。通常のPCAだと、標本数に比べて、値の列・次元が小さく、その場合には、その次元の数だけのeigenvaluesが出るが、関数解析の場合は、「標本数」「標本ごとの観測数」、その積が「観測値」になってくる。でも「観測しているのは、標本数」。そんなとき、観測値すべて分のeigenvaluesが出るわけはなく、たいては、「標本ごとの観測数」が多いので、0でないeigenvaluesは標本数に縛られる。今、分散を考えるときに「平均カーブ」を差し引いているから(たぶん、それが理由)、「標本数ー1」個のeigenvaluesが出る。今回の場合は20-1=19。となると、19個全部を使うのでは、情報を圧縮していないので、絞りましょう。それが「対数をとってその直線から外れているか」で判断しました、と言うのが、上の3の決め方のこと

par(mfcol=c(1,2))
plot(log(fdaeig.))
abline(v=19)
plot(log(fdaeig.[1:19]))
par(mfcol=c(1,1))
nharm <- 3
fdapcaList <- pca.fd(fdafd,nharm)
plot.pca.fd(fdapcaList)
fdarotpcaList <- varmx.pca.fd(fdapcaList)
plot.pca.fd(fdarotpcaList)
-
- PCAなので、「曲線のサンプルセット」に対して「中心」と、「中心からのずれ」がある
- 「中心」というのは、平滑化した後の曲線セットの平均
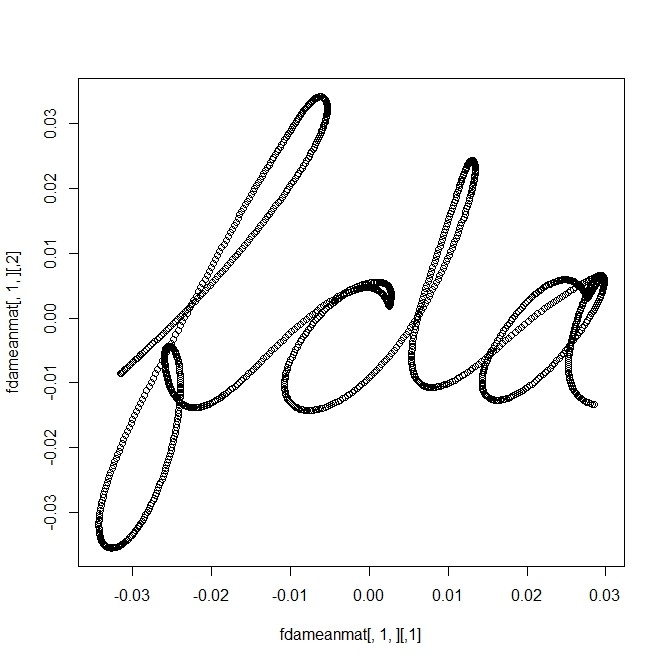
fdameanfd = mean(fdafd)
fdameanmat = eval.fd(fdatime, fdameanfd)
plot(fdameanmat[,1,])
-
- ここで「平滑化した曲線の平均としての曲線」というのは、平滑化した曲線が基底関数の係数ベクトルで表されているときに、その係数の平均を出すこと。やってみる
tmp.mean <- apply(fdafd$coefs,c(1,3),mean)
tmp.mean-fdameanfd$coefs[,1,]
-
- 「中心からのずれ」は「曲線にそって」全体にある。それぞれの箇所でのずれをつなぐと、曲線になるから、それを図示することもできる
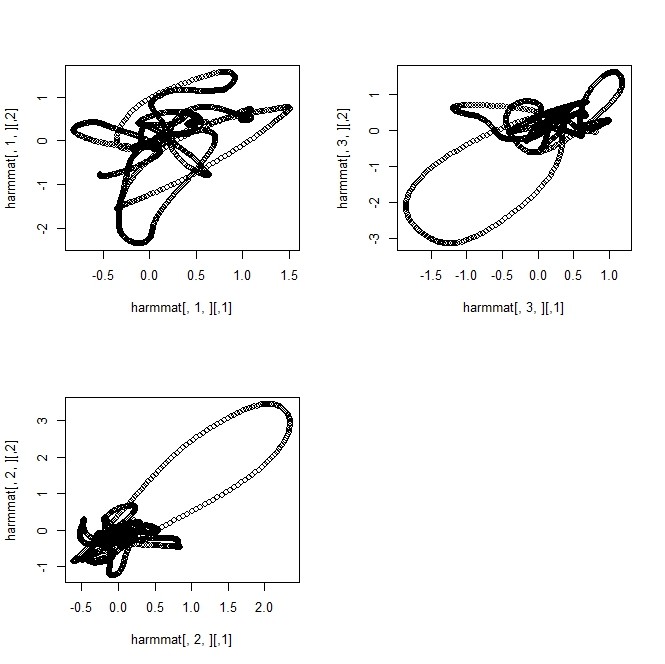
harmfd = fdarotpcaList$harm
harmmat = eval.fd(fdatime, harmfd)
par(mfcol=c(2,2))
plot(harmmat[,1,])
plot(harmmat[,2,])
plot(harmmat[,3,])
par(mfcol=c(1,1))
-
- 結局、pca.fd()の出力は
- harmonicsとよばれる、eigenfunctionsが、指定して個数。これは関数なので関数オブジェクトのリストとして返る
- valuesはeigenvaluesただし、harmonicsの数ではなくて、全eigenvaluesが返る
- scoresが、観測標本ごとの、harmonicsの重み係数を納めた行列
- meanfdは「平均カーブ」の関数オブジェクト








