行列演算としての２次元ウェーブレット変換

• ２次元画像のウェーブレット変換をしてみる
• Haarウェーブレットを例にとる
• waveslimパッケージを使えば

library(waveslim)
data(xbox)
X <- xbox
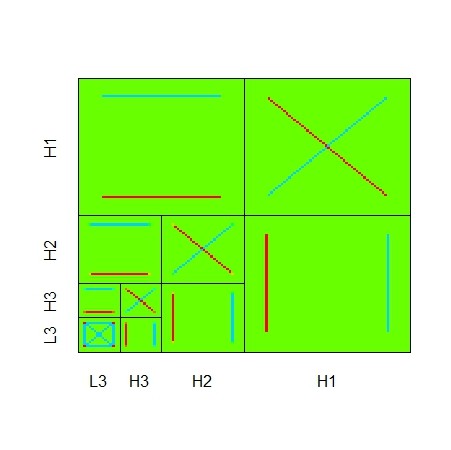
out.dwt <- dwt.2d(X,"haar",3)
dev.new()
plot.dwt.2d(out.dwt)
####
n <- 128
X <- matrix(rnorm(n^2),n,n)
ad <- which(X>0,arr.ind=TRUE)
v <- apply((ad-mean(ad))^2,1,sum)
X[which(v>mean(v))] <- 10
out.dwt <- dwt.2d(X,"haar",3)
dev.new()
plot.dwt.2d(out.dwt)

• 入力データがnxn行列で、出力もnxn行列なのでうまく行列演算で書いてみよう、という話
  • 以下の２図は行列計算だけで描いたもの

• コードを残して、考え方を確認
  • まずは、１回のウェーブレット処理をして、nxn行列を4つの(n/2)x(n/2)行列に分ける処理を関数化
  • ついで、１回処理を繰り返す関数を作る
• １回ウェーブレット

# X がnxn行列データ
my.dwt.2d.mx <- function(X,mx=my.dwt.mx(length(X[1,])),plot=TRUE){
# ユーティリティ行列の作成
	if(is.null(mx)){
		mx <- my.dwt.mx(length(X[1,]))
	}
# 4つの行列を作る
# それぞれの行列は、列に対するウェーブレット処理をXの左から、行に関する処理をXの右から施す
# さらに、外側から行位置変更・列位置変更の処理をするために、外側から行列をかける
# やることは列処理・行処理そのうち、2x2行列単位で１要素を抜き出す
# その上で、(n/2)x(n/2)要素以外は0とし
# 4つの行列から出てくる0とは限らない(n/2)x(n/2)個の要素を相互に重ならないように配置する
	XLL <- mx$N2 %*% mx$ML %*% X %*% t(mx$ML) %*% t(mx$N2)
	XHH <- mx$N1 %*% mx$MH %*% X %*% t(mx$MH) %*% t(mx$N1)
	XLH <- mx$N1 %*% mx$MH %*% X %*% t(mx$ML) %*% t(mx$N2)
	XHL <- mx$N2 %*% mx$ML %*% X %*% t(mx$MH) %*% t(mx$N1)
	X.all <- XLL + XHH + XLH + XHL
	if(plot){
		image(X.all,col = rainbow(128))
	}
	return(X.all)
}
# ユーティリティ行列を作る
# Haarウェーブレットに対応した行列、要素抜出・再配置の行列
my.dwt.mx <- function(n){
	MH <- ML <- N1 <- N2 <- matrix(0,n,n)
	for(i in 1:n){
		if(i==1){
			MH[i,i] <- c(1)
			ML[i,i] <- c(-1)
		}else{
			MH[i,(i-1):i] <- c(1,1)
			ML[i,(i-1):i] <- c(1,-1)
		}
		if(i <= n/2){
			N1[i,i*2] <- 1
			N2[i+n/2,i*2] <- 1
		}
		
	}
	M <- matrix(0,n,n)
	for(i in 1:n){
		M[i,n-i] <- 1
	}

	return(list(MH=MH,ML=ML,N1=N1,N2=N2,M=M))
}
# 実行
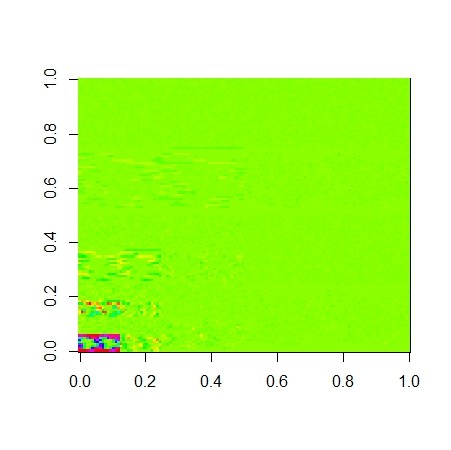
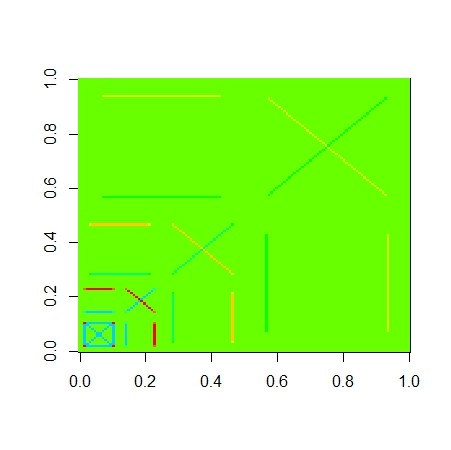
out <- my.dwt.2d.mx(X)

• 繰り返し処理
  • 繰り返し処理は、４分の１サイズの行列４個のうち、１個について取り出して、それにもう一度ウェーブレット処理をして、小行列４個で置き換える、ということの繰り返し

my.dwt.2d.mx.iter <- function(X,k,plot=TRUE){
	n <- length(X[1,])
	if(plot){
		M <- matrix(0,n,n)
		for(i in 1:n){
			M[i,n-i] <- 1
		}
	}
	for(i in 1:k){
		if(i==1){
			if(k==1){
				retX <- my.dwt.2d.mx(X,plot=plot)
			}else{
				retX <- my.dwt.2d.mx(X,plot=FALSE)
			}
			currentX <- retX[1:(n/2),1:(n/2)]
		}else if(i!=k){
			tmpX <- my.dwt.2d.mx(currentX,plot=FALSE)
			tmpn <- length(tmpX[1,])
			retX[1:(tmpn),1:(tmpn)] <- tmpX
			
			currentX <- tmpX[1:(tmpn/2),1:(tmpn/2)]
		}else{
			tmpX <- my.dwt.2d.mx(currentX,plot=FALSE)
			tmpn <- length(tmpX[1,])
			retX[1:(tmpn),1:(tmpn)] <- tmpX
		}
	}
	if(plot){
		image(retX,col=rainbow(128))
	}
	retX
}
out <- my.dwt.2d.mx.iter(X,3)