2020-05-03

乱数製造器としての確率変数

確率変数乱数

標準正規分布に従う乱数を作ってくれる製造器を標準正規分布確率変数と呼ぶ（と呼ぼう）
このように、問いかければ、何かを返してくれるもの、返してくれる何かが問いかけのたびに変わるもの、ただし、そこにはルールがある、そんなものが確率変数（としよう）
一般的な１次元実数確率変数としては、一様分布に従う乱数製造器などなど、ある
指数分布に従う乱数製造器も確率変数。これは、ちょっと面白い性質があって、ポアソン事象を連続して観測した時の、２つの事象の間の時間・距離がとる分布になっている
何が面白いかというと、「ある乱数製造器が作った、２つの距離」になっていること
乱数製造器は１つずつの乱数を独立に作ってくれるのにも関わらず、２つの乱数の距離になっている・・・１つなのに、２つ
こんなことを考えていた
量子確率論では、行列が確率変数になっている
行列をグラフの表現と見ると、グラフが確率変数になっている、とも見える
グラフがあった時、そこから、どんな乱数が製造できるだろうか？
ランダムに２点を取った時、２点間のグラフ距離はばらつく。この２点間グラフ距離のランダムな分布を作る製造器としてグラフを捉えれば、そのグラフはそのような距離分布をランダムに作ってくれる乱数製造器であり、そのような確率変数を体現していることになる。グラフ距離行列を作成し、そのセルの値をランダムに取り出せば良い（この極限が取れれば、曲面を乱数製造器とみなすこともできる）
量子確率論では、グラフの隣接行列を取り、その冪乗の標準化トレースをモーメントとする確率変数としてグラフを考える、という「定番」の確率変数がある
これは、k-次モーメントを、k歩で、元の頂点に戻ってくる歩道の数の平均値とするような確率変数として、グラフ隣接行列を見よう、ということ
グラフを乱数製造器とみなすなら、他にも色々できそうだ
k歩が気になるなら、任意の頂点ペアについて、k歩で行きあえる歩道の数というのも確率変数になる
さらに、k歩にこだわるなら、k歩進んで、結局、グラフ距離としてどれくらいの所にあるか、というのも確率変数になる
グラフのゼータ関数は、non-backtracking cycleに関する関数だが、non-backtracking cycleの長さに着目した確率変数の性質を考えていることだとわかる

2020-05-01

エッセンス：量子確率論

こちらで「量子確率論とその応用」をぱらぱらめくった
文書を抜き書きしただけで、特に数式についてはあえて端折った
この記事では、数式関連の抜き書きをする
直交多項式は以下のような漸化式で表される
- $P_0(x) = 1$
- $P_1(x) = x - \alpha_1$
- $P_{n+1}(x) = (x-\alpha_{n+1})P_n(x) + w_n P_{n-1}(x)$
ここで、 $\{\alpha_n\}_{n=1}^{\infty}, \{w_n\}_{n=1}^{\infty}\}, \alpha_n \in R, w_n \ge 0$ がヤコビ系数列
ヒルベルト空間の正規直交基底があって、それらは、３つの作用素によって以下のような関係にある
- $B^+ \Phi_n = \sqrt{w_{n+1}} \Phi_{n+1}$
- $B^- \Phi_0 = 0, \; B^- \Phi_n = \sqrt{w_n} \Phi_{n-1}$
- $B^o \Phi_0 = \alpha_{n+1} \Phi_n$
また、次のような関係がある
- $U : \Phi_n \to \frac{1}{\sqrt{\prod_{i=1}^n w_i}} P_n$
で、モーメントは
- $E(X^m) = \int_{-\infty}^{\infty} x^m \mu (dx)= < P_0, Q^m P_0 > = < \Phi_0, (B^+ + B^o + B^-)^m \Phi_0 >$
Rのorthopolynomパッケージを使うと、直交多項式が作れる

library(orthopolynom)
p.0 <- polynomial( c( 1 ) )
n <- 10
# ckpk+1 (x) = (dk + ekx) pk (x) − fkpk−1 (x)
# rec should specify ck,dk,ek and fk
# p_(n+1) = (x-alhap_n) p_n + w_(n-1) p_(n-1) が作りたい
rec <- data.frame(c=rep(1,n),d=-rnorm(n),e=rep(1,n),f=runif(n))
p.list <- orthonormal.polynomials( rec, p.0 )
p.list
x <- seq(from= -1,to=1,length=101)
ys <- polynomial.values(p.list,x)
ys.mat <- matrix(unlist(ys),ncol=length(p.list))
matplot(x,ys.mat,type="l")

f:id:ryamada22:20200502120320p:plain

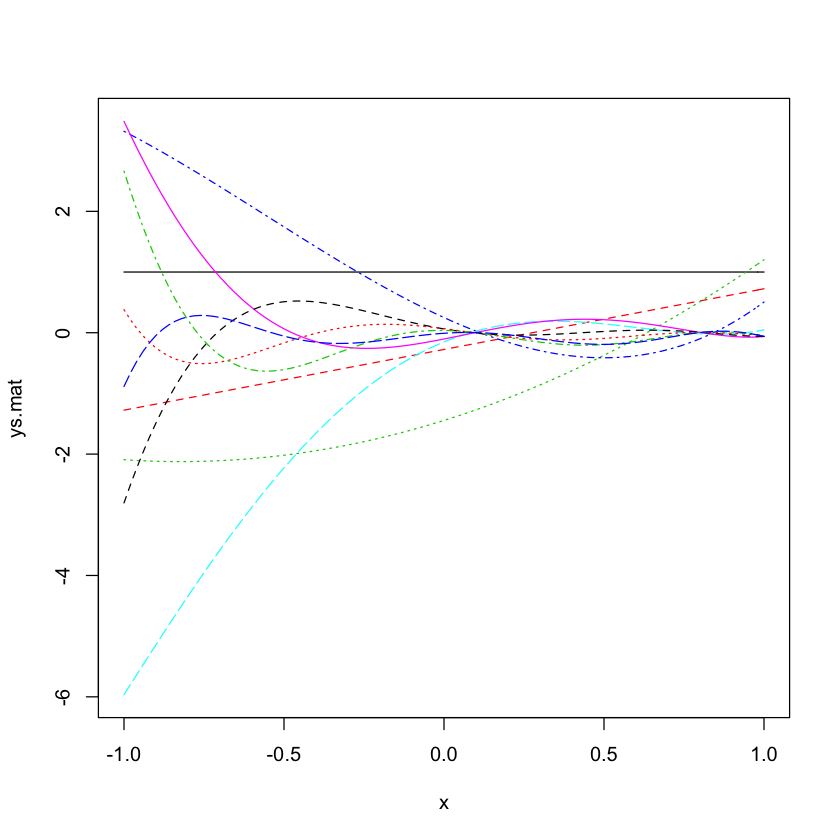
こんな問題設定
- ある関数V1とV2とがある
- 何かの拍子で、それらと正規直交基底のそれぞれとの内積がわかったとする
  - この２つの関数の正規直交基底との内積が、それぞれの「モーメント」から算出できるとき、それぞれのモーメント列がわかれば、その確率関数ペアの内積は求まりそうだ・・・
- その時、V1とV2との内積は $V1^T V2 = (V1^T R) (V2^T R)^T = V1^T R R^T V2 = V1^T I V2$ なので
- ちょっと有限次元でやっておく

d <- 3
R <- GPArotation::Random.Start(d)
V1 <- rnorm(d)
V2 <- rnorm(d)
sum(V1*V2)
IP1 <- matrix(V1,nrow=1) %*% R
IP2 <- matrix(V2,nrow=1) %*% R
sum(IP1 * IP2)

> sum(V1*V2)
[1] -1.460819
> IP1 <- matrix(V1,nrow=1) %*% R
> IP2 <- matrix(V2,nrow=1) %*% R
> sum(IP1 * IP2)
[1] -1.460819

より具体的には、区間を決めて、その範囲で定義した多項式を使う（ことが多い）。Legendre polynomialsはその一例

2020-04-27

ぱらぱらめくる『量子確率論とその応用』　再び

量子確率論ぱらぱらめくるシリーズ

このPDF『量子確率論とその応用』は、１年ほど前に、読みかじったのだが、消化不良だった。
再読を試みる異にする
いつものごとく、自分の興味・目的に引きつけて読む事になるが、１年前と今とで、何が違うかというと、行列の集合を比較することへの興味が強くなったことだろうか
例えば、こちらのarXivペイパー(Comparing lar-gegraphs based on quantum probability theory)のようなことに対する具体的興味が強くなっており、それが、今回の再読の動機になっている
このarXivペイパーを簡単に紹介すると…
- グラフの行列表現として隣接行列を考える。グラフ・スペクトルによる、グラフ間の異同の評価は、行列の固有値列の比較にすぎなくて、弁別力が不足している
- それは、量子確率論でいうと、正方行列Aが会った時に $A^k$ を考えるのだが、そのトレースだけを気にしているのでは、固有値セットのみが情報量の全てになってしまうところ、 $A^k$ のトレース以外を取り出す（トレースを取り出すのも、トレース以外を取り出すのも、量子確率論では、状態と呼ばれる関数の仕事なので、「量子確率論の状態」を切り替えることに相当）ことで、Aの持つ情報を豊かにできることを書いている
- $A^k$ が何を表すかをグラフに即して少し補足すると、 $A^k[i,j]$ は、頂点iから頂点jへのk歩の行き方の場合の数。したがって、 $A^k$ を使った量子確率論的k-次モーメントは、２頂点間のk歩パスの数の期待値となる
このように、確率変数の「モーメント」に具体的な意味が見えてきたことで、量子確率論の枠組みで考えることへの興味が一新された、とそんなところ
さて。再読
目次
- １　量子確率論の基礎概念
- ２　量子分解
- ３　代数的グラフ理論
- ４　スペクトル・グラフ理論
- ５　大きなグラフの漸近的スペクトル解析
１　量子確率論の基礎概念
- 代数的確率空間
  - *-代数とその上で定義された状態の組が代数的確率空間、ただし、は*-代数、は状態と呼ばれる関数で、
    - ここで、具体的なものがないとイメージが湧かないので…。*-代数の好例は、複素正方行列全体、状態の例としては、行列を引数にして、その標準化トレース(トレースを次元で割ったもの、以下、Trは標準化トレースを表すものとする)を返す関数がある。ちなみに、量子確率変数の中に、実確率変数が含まれるが、実確率変数は、複素行列のうち、エルミート行列に対応する
    - 「確率」っぽさはどこからくるかと言うと：状態と言う関数は、*-代数の要素 $a$ に対して $\psi(a^*a) \ge 0$ となると言う条件がある…これが、「至るところで正」であると言う確率っぽさをもち、 $\psi(1_A) = 1$ (単位行列 $1_A$ )と言う性質は、 $\psi(a^k)$ をk-次モーメントを返す関数だと見た時に、 $\psi(A^0) = \psi(1_A) = \int p(x) dx = 1$ となって、全確率を足すと１、と言う確率変数っぽさをもつ、この２点、か。
    - 状態に純粋状態と混合状態とがあると言う概念は、量子統計力学的な側面の印象がある
  - 複素正方行列を*-代数とする状態には、密度行列が１対１対応する。 $\psi(a) = Tr(\rho a),\psi(\rho a^k) = Tr(\rho a^k)$ 。この密度行列は正定値行列であって、 $Tr(\rho)=1$ になると言う。後者は $\psi(1_A) = 1$ から要求される。前者は「至るところで正」であると言う確率っぽさの条件に対応する
  - 密度行列はどうしてあるか…。量子力学では、純粋状態と言うものがあり、また、純粋状態がある割合で混ざった混合状態と言うものもある。この混合状態は、状態を並べて、それぞれに、確率を割り当てる、と言う形で記載できるが、これだと、２本のベクトルで書ける。物理学において実験的に観測をすると、物理量がこれこれの値をこれこれの確率で取る、と言う形で観測される。しかし、この観測される分布は、色々な混合状態に対応していて、区別ができない。区別するにはどうするか、と言うと、密度行列として表すことで解決する。解決すると言うことは、２本のベクトルで書けていたものが、正方行列に相当するたくさんの情報を持つものとして表して区別すると言うことである。しかし、物理観測では、区別がつかないので、この区別されて異なる密度行列から、同一の確率分布が観察されるべきである。この情報が落ちてしまう、観測確率が $Tr(\rho A)$ である。区別されるべきだが、観測するとトレースしかわからない、と言うところで情報が落ちている
  - 密度行列はnxnなので情報量は多いが、ランクを考えると、ランクが1のこともあるし、nのこともある。ランクが1の行列は、成分数こそnxn個あるが、n次元ベクトルのouter積になっているもののことであるから、n個の値で決まる。このような密度行列は純粋状態に対応する密度行列になっている、と言う性質もある
  - 密度行列とはそんな役どころのもの（らしい）
２　量子分解
- 実確率変数について考える。モーメント列が得られた時にどうするかと言う話
- モーメント列を扱うための「直交多項式」があると便利
  - 確率測度 $\mu$ のモーメントのためにある多項式列なので、「 $\mu$ に付随する直交多項式」と呼ばれる
  - モーメント列を扱うには $x^0=1,x,x^2,x^3,...$ が扱いたい。このxのk次単項式そのままを使うと、単項式関数同士が直交関係にないので、使いにくい。そこで、直交多項式の系列を作りつつ、モーメント列を扱うことができるような仕組みが作りたくなる。そんな話
- ベクトルの集合から直交ベクトル集合を作る方法にグラム・シュミットの直交化法こちらがある。順番に単位ベクトルを作る、次の単位ベクトルを作るにあたって、それまでに登録された単位ベクトルと直交しない成分を差し引くことで、「残り成分」を追加するべき単位ベクトル方向にする、と言う方法である
- これを関数について行えば、直交関数集合が取れる
- 直交多項式は、ヤコビ係数列と呼ばれる二種類の係数列に情報を持たせることができるのだが、そのヤコビ係数列が「きれい」な直交多項式にチェビシェフ多項式と呼ばれるものがある。これは三角関数の位相を整数倍した関数が、位相１倍の三角関数の多項式となっていることを示した多項式で、ヤコビ係数列がキレイ
- ヤコビ係数列は、次の３項間漸化式の係数でもある
  - $P_0(x)=1,P_1(x) = x- \alpha_1,xP_n(x) = P_{n+1}(x) + \alpha_{n+1} P_n(x) + w_n P_{n-1}(x)$
  - $||P_0(x)|| = 1, ||P_n(x)|| = \sqrt{\prod_{i=1}^n w_i}$
  - $\alpha_1$ は期待値で、 $w_1$ は分散になってもいる
- モーメント列から確率測度・確率密度を逆算するのは、一般に大変。な、の、で、うまく逆算できるものを作って見ようと考えてみる。モーメント列そのものからの出発もちょっと面倒なので、モーメント列とヤコビ係数列とが１対１対応であることを利用して、ヤコビ係数列から確率密度を逆算してみる。さらに、制約を課して、ヤコビ数列の自由度をぐいっと抑えてやることにする。その例として、平均を０に指定(ここをパラメタ指定することもあるようだ）、分散には自由度を与えて指定、（したがって、ヤコビ係数列の第１成分がそれぞれ決まる）、その上で、ヤコビ係数列のそのほかの値は、一定にする（自由度２）。このような制約のきついヤコビ係数列に対して、決まる確率密度分布が自由マイクスナー分布。結局、分散pと、ヤコビ係数列の大多数の値を固定的に指定するa,qとの３変数（平均をパラメタ指定する場合は４変数）で決まるのがマイクスナー分布(参考)
- 相互作用フォック空間というものが出てくる
  - ２つのヤコビ係数列が両方、登場する関係、というような意味合いで「相互作用」と称するのだと思う
  - そもそも、ヤコビ係数列は、モーメント列を扱うにあたって登場した関数列 $1,x,x^2,x^3,...$ から直交関数列 $P_i(x)$ を作ることと関係していた
  - 今、ヒルベルト空間に正規直交基底を取ることを考える。このヒルベルト空間正規直交基底は、ヤコビ数列と関係する。直交基底のそれぞれはベクトルのようにも見えるし、（無限次元）ヒルベルト空間だと、関数のようにも見える。直交関数列なら、 $P_i(x)$ もそうだったから、このヒルベルト空間に取らんとする正規直交基底は直交関数列 $P_i(x)$ と関連の深いもののように見える
  - このヒルベルト空間正規直交基底の要素間の関係をヤコビ係数列を用いて結びつけるにあたり、３つの線形作用素 $B^+,B^-,B^o$ を用いれば良いらしい。その時に気にするのは、 $||P_n(x)|| = \sqrt{\prod_{i=1}^n w_i}$ が関係する
  - いずれにしろ、ヒルベルト空間正規直交基底が、ヤコビ係数列に３つの線形作用素を追加することで得られ、それは、モーメント系列のための直交関数列の影武者のような存在だと言えそうだ
  - 実際、この直交関数列 $P_i(x)$ とヒルベルト空間の正規直交基底は「等距離作用素」と呼ばれるもので対応づけされる
  - 結局、ヤコビ係数列が与えられた時に、そこから、ヒルベルト空間と、正規直交基底と、３つの線形作用素（生成作用素と消滅作用素と保存作用素という名がそれら３つにはついている）
  - 正規分布やベルヌーイ分布などが、この相互作用フォック空間に「真空ベクトル（ヒルベルト空間の正規直交基底の第１基底）」を組み合わせて得られる「相互作用フォック確率空間」の例になっている
    - $\int_{-\infty}^{\infty} x^m \mu(dx) = < P_0, Q^m P_0 > = <\Psi_0, (B^+ +B^o + B^-)^m \Psi_0>$
  - ただし、単純な実確率変数の場合２つのヤコビ係数列のうち、片方は０で、もう片方も、ごく単純(1,2,3,...,とか、0,1,0,1,...とか、1,1,1,1...とか)
３　代数的グラフ理論
- 隣接行列
- 隣接行列を置換行列でサンドイッチすることは頂点IDの付け方の変更に相当し、グラフとしては同一のものを表している
- 隣接行列の冪乗に係数をかけて足し合わせてできる行列全体は隣接代数をなす→行列の冪を考えてモーメントを取るあたりで、量子確率的
- 隣接行列は特性多項式を持つ
- パスグラフというのは、１本道状のグラフ。パスグラフの長さを伸ばしていくと、グラフの系列ができるが、それに対応して特性多項式の系列もできる。このパスグラフの特性多項式の系列は第二種チェビシェフ多項式を用いて表現できる
- グラフは行列で、それが直交多項式と関係する
- 量子確率論では、行列からモーメント列が出て、直交多項式があり、ヤコビ係数列が出てきた。その関係と絡んでくる話をしているのだと思われる
４　スペクトル・グラフ理論
- グラフのスペクトルは、隣接行列の(正の固有値)の昇順列と、それぞれの固有値の個数のベクトルとのペアで表すことが多い
- グラフの固有値のところにデルタ関数があるとみなせば、グラフのスペクトルは、デルタ関数がぽつぽつと立った「確率分布」となる。これがスペクトル分布
- スペクトル分布を代数的確率空間で扱うことが論じられる
- 代数的確率空間では、ヒルベルト空間直交基底を使って議論したが、それは、グラフのある頂点をヒルベルト空間直交基底の一つの基底である真空状態ベクトルに対応させたときに相当し、モーメントが定まる。このモーメントは、指定した頂点を出発して自身に戻る歩道の個数になっている
- グラフの隣接行列、そのべき乗が作る接続代数が何を表しているかというと、真空状態を基点とした、ヒルベルト空間直交基底が、グラフ距離ごとに頂点をグループ分けすることに相当し、 $B^+,B^-,B^o$ 的な表現と対応する(らしい)こと
- このようなグラフのスペクトル分布を量子確率空間的に扱い、グラフを分解して考えることは、規則的なグラフにおいてその漸化式や、真空状態、ヤコビ係数列が調べられている。

2020-02-20

ランダム行列とその応用

ランダム行列理論ランダム行列スペクトル固有値

参考文献

2020-02-18

推定。パラとノンパラ

ガウシアンカーネル分布推定パラメトリックノンパラメトリックバイアス・バリアンスオーバーフィッティング

混交正規分布が背景にあるとする
パラメトリックに、単純な正規分布を仮定して、推定すると、サンプル数を増やしても、推定結果は1峰性の正規分布であり、背景分布の平均（期待値）と分散は正確になるが、混合正規分布の特徴である複数峰は決して推定されない。
また、期待値と分散の推定値は、散布する数が少ないときから安定して、よい値が推定される
この、サンプル数が少ないときから、（モデルとしては不十分ながら）推定結果がよいことを、推定のバリアンス（ばらつき）が小さく収まるという
その一方で、サンプル数をどんなに増やしても、真の分布である複数峰には近づかないことを、「モデルが真からずれている」から「推定結果もずれざるを得ない」と言う意味で、バイアスが大きい推定になっている、と言う
他方、ガウシアン・カーネルによる密度推定では、個々のサンプルに小さな正規分布を担わせ、それらの加算として、全体の密度分布を推定させる。したがって、サンプル数が大きくなればなるほど、たくさんの小正規分布の和として分布推定される。使用するパラメタ数が大きくなるともいえる
この、サンプル数が増えれば増えるほど、分布を説明するパラメタ数が大きくなる推定法であることを「ノンパラメトリックな推定手法」である、と言う。
しかしながら、個々のサンプルに担わせる小さな正規分布をどんなものにするかに選択の余地があり、その選び方で結果が変わる。ガウシアンカーネル法の場合には、平均は観測値そのものとするとして、分散をどうするかは選ばないといけない
その分散を大きくしすぎると、背景分布の細かい多峰性は表現できないし、分散を小さくしすぎると、全体の様相をつかみ損ねて、標本依存性が上がる。この標本依存性が上がってしまうことを、オーバーフィッティングと言ったり、推定のバリアンスが大きいと言ったりする
しかしながら、パラメトリックな手法の際に、バイアスは大きくてもよいからバリアンスを小さく維持することに成功したことの裏返しで、バリアンスは大きくなるが、バイアスは小さくできる。したがって、標本数が大きいときには、標本数がバリアンスを押しとどめてくれるので、バイアスの小さい、真の分布に近いものを得うる、という可能性をもつ
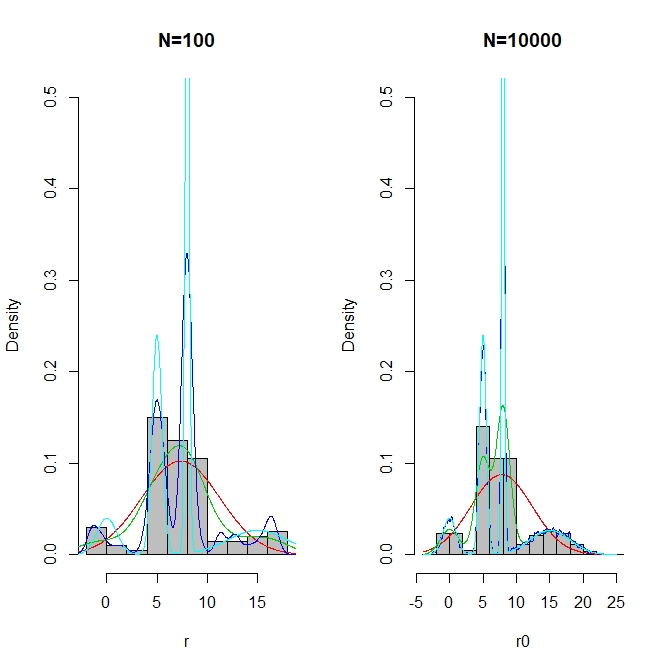
以下のＲコードは、４峰性の1次元混合正規分布に対して、単純な１峰性正規分布推定をパラメトリックな推定法の代表として用い、ガウシアンカーネル法をノンパラメトリックな手法として用いつつ、ガウシアンカーネルの個別分布の分散に大小２つを採用することで、サンプル数の多寡による推定分布の変化の様子を見ている
Ｎが小さくても大きくても、1峰パラメトリック推定（赤）は大して変わらない・・・バリアンスが小さい
Ｎが小さいときと大きいときでも、緑の推定（ガウシアンカーネルで分散が大きめ）は滑らかな推定分布であるが、方や、中央付近に大きな１峰、方や、中央付近に2峰の可能性の萌芽が見える
分散の小さいガウシアンカーネルの場合は、Ｎが小さくても、大きくても、中央付近にシャープな2峰が推定できている点では、よい推定だが、Ｎが小さいときに、左右の裾領域に複数の峰が現れており、真分布に合致せず、標本に引きずられている様子が見える（バリアンスが高い）