フェノタイプの整理メモ１１ 確率的に考える６

• ステージ評価するフェノタイプ
• ステージ評価型のフェノタイプは、順序があり、ステージの差異は、多くの場合、質的な違いによる
• また、ステージの逆行は考慮しないものが多い
• これをモデル化することを考える
• ステージからへの移行にあたっては、これまでに考えてきた0/1型フェノタイプとその背後にある複数イベントの蓄積を用いることができる
• シミュレーションモデルとしては２つ考えられそうだ
  • １次元軸進行・多ステージモデル
  • 階層化モデル
• １次元軸進行・多ステージモデル
  • ある１種類のイベントの蓄積が進み、その途中に、ステージを上る閾値が何箇所かある
• 階層化モデル
  • からへと進むときに、それぞれの段階で多数の「病変」の形成を伴い、一定数以上の「病変」が生じたときに、ステージを上がる。この場合、「病変となりうる箇所数」が階層的に束ねられており、シミュレーション上、少し面倒くさい
• この記事では、１次元軸進行・多ステージモデルでやってみよう。パラメタ化するのは次のようなものになろう
  • イベントの発生頻度に個人差があり
  • ステージ切り替えの閾値の多寡に個人差がある

# マルチステージ

NL<-1 # 座位数
TL<-120 # 一生は120年

Fs<-0.01*2^(9.5) # イベントが起きる平均時間間隔(年)

ThresNums<-c(10,15,17,21)

Nstage<-length(ThresNums)

DxTimes<-matrix(0,Niter,length(ThresNums))
par(ask=FALSE)
for(fi in 1:length(Fs)){
	F<-Fs[fi]
	#ThresNum<-ThresNums[1]

	Niter<-1000
	
	for(ii in 1:Niter){
		NR<-max(ThresNums)
		Rmat<-matrix(0,NL,NR)
		for(i in 1:NL){
			Rmat[i,]<-rexp(NR,1/F[i])
		}
		CumEventMat<-t(apply(Rmat,1,cumsum))

		#DxTime<-rep(0,NL)
		#for(i in 1:NL){
			DxTimes[ii,]<-CumEventMat[i,ThresNums]
		#}
		#DxTimes[ii,]<-DxTime
	}

	hist(DxTimes[,1],breaks=0:ceiling(max(DxTimes[,1])),xlim=c(0,TL),
	xlab="Age of Dx(year)",ylab="Fraction of Dx",col=2,freq=FALSE)

#plot(ecdf(DxTimes[,1]),xlim=c(0,TL))
}

par(mfcol=c(2,2))
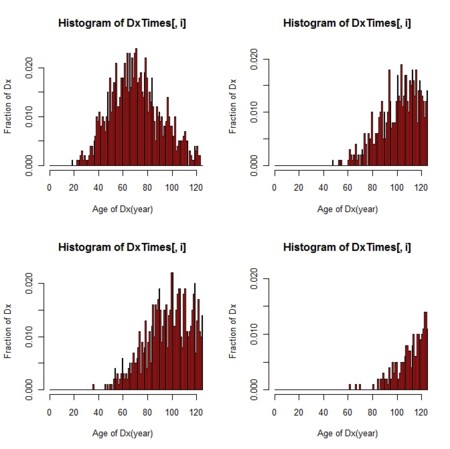
for(i in 1:4){
	hist(DxTimes[,i],breaks=0:ceiling(max(DxTimes)),xlim=c(0,TL),
	xlab="Age of Dx(year)",ylab="Fraction of Dx",col=2,freq=FALSE)
}
par(mfcol=c(1,1))

#par(mfcol=c(2,2))
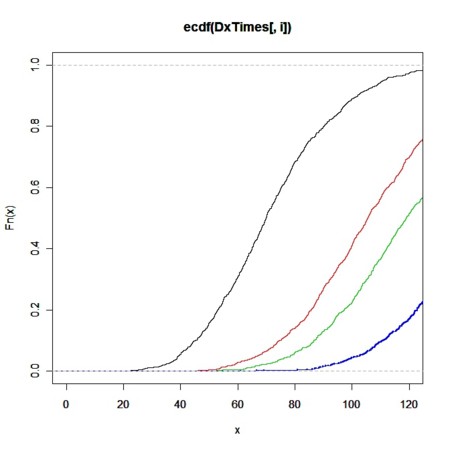
for(i in 1:4){
	plot(ecdf(DxTimes[,i]),xlim=c(0,TL),cex=0.1,ylim=c(0,1),col=i)
	par(new=TRUE)
}
#par(mfcol=c(1,1))