2011-10-02

フェノタイプの整理メモ　１５　確率的に考える１０

ネットワークの因子たち(ロトカ=ヴォルテラ編)
多くの分子はネットワークを形成し、フィードバック等の制御構造がある
単純な構造として、ロトカ=ヴォルテラ(たとえばこちら)のような反応ループ関係を取り上げる
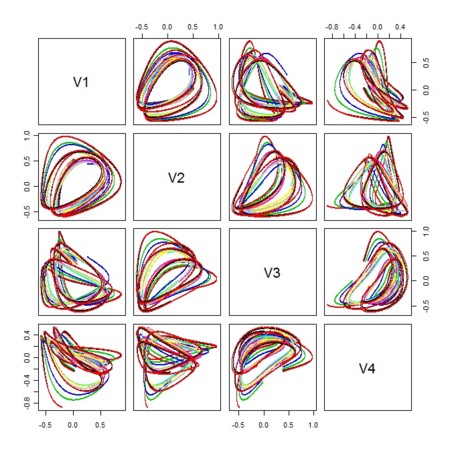
初期値が異なるだけで、ループの構成因子の濃度分布は異なってくる
個体差はこんなところにもあり、ジェノタイプによって、ループ構成因子の(ある時点の)濃度が定まれば、その後の周期的変動には個体差があり、それは、個々の因子の濃度の平均・分散・最大・最小などに影響を及ぼす

library(sphere)
library(rgl)
StandardLotkaVolterra20111005<-function(n=4,Nrep=30,drift=FALSE,driftk=0.05,Niter=1000,dt=0.01,us=NULL){
	if(is.null(us)){
		us<-rep(1,n)
		#us<-sample(1:10,n) # それぞれの種の単位Pあたり個体数
	}

# 捕食・被捕食関係の数Nrは種の数と同じ
Nr<-n
# 捕食・被捕食効率
ks<-runif(Nr)
ks<-rep(1,n)
# Inは被捕食種。１度の出会いで殺される個体数
# Playerは捕食・被捕食関係で参加する種とその個体数
# 今は１捕食個体と１被捕食個体の出会いとする
# Outは出会いの結果生じる種とその個体数
# 今は捕食者
In<-Player<-diag(n)
Out<-matrix(0,Nr,n)
for(i in 1:Nr){
	for(j in 1:n){
		if(j==i+1){
			Player[i,j]<-1
			Out[i,j]<-1
		}
	}
}
Player[Nr,1]<-Out[Nr,1]<-1

S<-1
P<-runif(1,min=0,max=(1/n)^n)

xssum<-NULL
col<-c()
m<-matrix(Niter,n)
for(rep in 1:Nrep){
	# ここから時系列シミュレーション
	if(drift){
		if(rep>1){
			prevm<-m
		
			m<-prevm

			p<-rep(0,Niter)
			p[1]<-0
			for(i in 1:n){
				p[1]<-p[1]+us[i]*m[1,i]
			}
			m[1,]<-m[1,]/p[1]
			p[1]<-0
			for(i in 1:n){
				p[1]<-p[1]+us[i]*m[1,i]
			}
			m[1,]<-prevm[1,]+abs(rnorm(n)*driftk)
		}else{
		m<-matrix(0,Niter,n)
		p<-rep(0,Niter)
		p[1]<-0
		for(i in 1:n){
			p[1]<-p[1]+us[i]*m[1,i]
		}
		m[1,]<-m[1,]/p[1]
		p[1]<-0
		for(i in 1:n){
			p[1]<-p[1]+us[i]*m[1,i]
		}
		m[1,]<-runif(n)
		}
	}else{
		m<-matrix(0,Niter,n)
		p<-rep(0,Niter)
		p[1]<-0
		for(i in 1:n){
			p[1]<-p[1]+us[i]*m[1,i]
		}
		m[1,]<-m[1,]/p[1]
		p[1]<-0
		for(i in 1:n){
			p[1]<-p[1]+us[i]*m[1,i]
		}
		m[1,]<-runif(n)
	}
	

#p<-rep(0,Niter)
#p[1]<-0
#for(i in 1:n){
#	p[1]<-p[1]+us[i]*m[1,i]
#}
#m[1,]<-m[1,]/p[1]
#p[1]<-0
#for(i in 1:n){
#	p[1]<-p[1]+us[i]*m[1,i]
#}
library(MCMCpack)

#initloop<-TRUE
#while(initloop){
#	m[1,1]<-runif(1)
#	m[1,2]<-runif(1)
#	tmp1<-1-(m[1,1]+m[1,2])
#	tmp2<-tmp1^2-4*P/(m[1,1]*m[1,2])
#	if(tmp2>=0){
#		m[1,3]<-1/2*(tmp1+sqrt(tmp2))
#		m[1,4]<-1/2*(tmp1-sqrt(tmp2))
#		if(m[1,4]>0){
#			initloop<-FALSE
#		}
#	}
#	
#}
#m[1,]<-sample(m[1,])
#m[1,]<-runif(n)
for(i in 2:Niter){
	m[i,]<-m[i-1,]
	for(j in 1:Nr){
		tmp<-ks[j]*dt
		pamountIn<-0
		pamountOut<-0
		for(k in 1:n){
			tmp<-tmp*m[i-1,k]^Player[j,k]
			pamountIn<-pamountIn+us[k]*In[j,k]
			pamountOut<-pamountOut+us[k]*Out[j,k]
		}

		for(k in 1:n){
			m[i,k]<-m[i,k]-In[j,k]*tmp+tmp*pamountIn/pamountOut*us[k]*Out[j,k]/pamountOut*Out[j,k]
		}
	}

	for(j in 1:n){
		p[i]<-p[i]+us[j]*m[i,j]
	}

}
#plot(p,type="l",ylim=c(0,2),main="保存量")
#plot(data.frame(m),cex=0.1)
xs<-matrix(0,Niter,n-1)
cv<-CategoryVector(n)
for(i in 1:Niter){
	for(j in 1:n){
		xs[i,]<-xs[i,]+m[i,j]*cv[j,]
	}
}
xssum<-rbind(xssum,xs)
col<-c(col,rep(rep,Niter))
}

plot3d(xssum[,1],xssum[,2],xssum[,3],col=col)

list(X=xssum,col=col,In=In,Player=Player,Out=Out,m=m)
}
LV.out<-StandardLotkaVolterra20111005(n=5,Nrep=10,drift=TRUE)
plot(as.data.frame(LV.out[[1]]),col=LV.out[[2]],cex=0.01)