2011-11-06

単調増加の検出と比較（７）Isotonic programming のためのRのパッケージ・関数(IsoGene,pava()とquadprog,solve.QP())について

単調増加の検出と比較の目次
さて、実際にRに実装されているパッケージ・関数でやってみよう
最小化されるべき関数を $f(x)=\frac{1}{2}x^T Dmat x + dvec^T x$ とする
制約は、に関する等式と不等式とで表される
- 等式で表される制約meと不等式で表される制約mとがあって、併せてM=me+mとする
- 今回の例では、me=0
- 変数n、制約の個数M=mについて、M x n 行列 Amat2があって、 $Amat2^T x \le bvec$ が制約となる
- 以降で用いるquadprogパッケージのsolve.QP()関数の場合には、等式制約と不等式制約とを両方合わせて M x n 行列にしたうえで、どれが等式制約でどれが不等式制約であるのかをプログラムに引数指定する仕組みを取っている
データを作って

library(IsoGene)
library(quadprog)
# 観測用量点の数N
N<-10
# M本の用量反応曲線
M<-4

# データを作ろう
D<-matrix(0,N,M)
D[,1]<-sort(runif(N),decreasing=TRUE)+1

for(i in 2:M){
	k<-0.2
	D[1,i]<-D[1,1]*(runif(1)*k+(1-k))
	for(j in 2:N){
		D[j,i]<-min(D[j-1,i],D[j,1])*(runif(1)*k+(1-k))
	}
}


# データをばらつかせよう
# ばらつきの係数
r<-0.3
D2<-D+rnorm(N*M,sd=sqrt(var(D))*r)

プロットしてみる

# ばらつきを入れる前の値とばらつかせた後の値とをプロットする

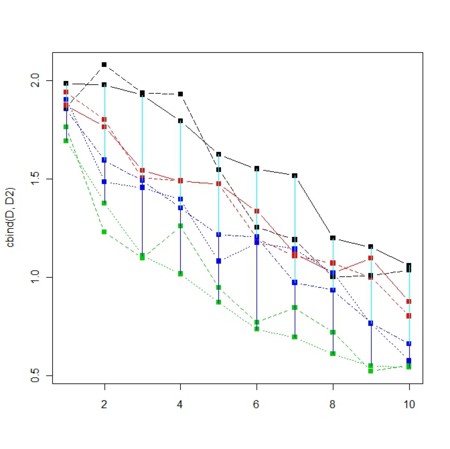
matplot(cbind(D,D2),type="b",pch=15,col=c(rep(1:M,2)))

for(i in 1:N){
	for(j in 2:M){
		segments(i,D[i,1],i,D[i,j],col=1+j)
	}
	
}

Dmatはnxn正方行列で、今回の場合、 $x_i^2$ はiによらず一定なので

# Dmat
# すべてtriplicateとする
ws<-rep(3,N*M)
Dmat<-diag(ws)

dvecの方がデータを反映する。きれいなデータとばらつかせたデータで異なるdvec

# dvec
dvec<-ws*c(D)
dvec2<-ws*c(D2)

制約条件行列を作ろう

# Amat
Q<-NULL
for(j in 1:M){
	for(i in 1:(N-1)){
	
		st<-(j-1)*N + i
		end<-st+1
		tmp<-rep(0,N*M)
		tmp[st]<-1
		tmp[end]<--1
		Q<-rbind(Q,tmp)
	}
}
for(i in 2:M){
	for(j in 1:N){
		st<-j
		end<-N*(i-1)+j
		tmp<-rep(0,N*M)
		tmp[st]<-1
		tmp[end]<--1
		Q<-rbind(Q,tmp)
	}
}
Q
Amat2<-Q
Amat<-t(Amat2)

制約条件のbvec

# bvec
bvec<-rep(0,length(Amat[1,]))

さて、解こう

# Dmat,dvec,Amat,bvecはそのまま
# meqは制約条件のうち、等式である数。今回は0
out1<-solve.QP(Dmat,dvec,Amat,bvec=bvec,meq=0)
out2<-solve.QP(Dmat,dvec2,Amat,bvec=bvec,meq=0)

結果

> out1
$solution
 [1] 1.7606338 1.5881934 1.5344888 1.4592201 1.3439146 1.2502945 1.1429360 1.0838089 1.0694384 1.0424076
[11] 1.7213358 1.5009083 1.4585956 1.4119514 1.1144510 0.9078028 0.7854388 0.6350420 0.6181277 0.6076870
[21] 1.4162341 1.2329624 1.1962830 1.1570695 1.0061177 0.8408625 0.8052883 0.6720841 0.5707691 0.4617527
[31] 1.4228720 1.2459309 1.1158810 1.0977527 0.9282307 0.8692899 0.7723391 0.7202274 0.5788950 0.4863466

$value
[1] -25.17345

$unconstrained.solution
 [1] 1.7606338 1.5881934 1.5344888 1.4592201 1.3439146 1.2502945 1.1429360 1.0838089 1.0694384 1.0424076
[11] 1.7213358 1.5009083 1.4585956 1.4119514 1.1144510 0.9078028 0.7854388 0.6350420 0.6181277 0.6076870
[21] 1.4162341 1.2329624 1.1962830 1.1570695 1.0061177 0.8408625 0.8052883 0.6720841 0.5707691 0.4617527
[31] 1.4228720 1.2459309 1.1158810 1.0977527 0.9282307 0.8692899 0.7723391 0.7202274 0.5788950 0.4863466

$iterations
[1] 1 0

$Lagrangian
 [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[52] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

$iact
[1] 0

> 
> out2
$solution
 [1] 1.8479498 1.5062915 1.5062915 1.4910746 1.3453317 1.1982639 1.0845460 1.0845460 1.0845460 1.0845460
[11] 1.7073539 1.5062915 1.5062915 1.4519923 0.9273577 0.9273577 0.7169679 0.7169679 0.6646322 0.6646322
[21] 1.2745786 1.2606716 1.2606716 1.2606716 0.9175620 0.9175620 0.9175620 0.6482105 0.6482105 0.6482105
[31] 1.2877883 1.1185829 1.0685545 0.9041312 0.8946122 0.8946122 0.7074181 0.7074181 0.5164071 0.4327213

$value
[1] -24.71127

$unconstrained.solution
 [1] 1.8479498 1.4801033 1.4579306 1.4910746 1.3453317 1.1982639 1.0813759 1.0341926 0.9415810 1.2810346
[11] 1.7073539 1.5149246 1.5722076 1.4519923 0.8326514 1.0220641 0.7111795 0.7227562 0.6261859 0.7030785
[21] 1.2745786 1.1908582 1.2852327 1.3059240 0.8881577 0.9410679 0.9234605 0.6031618 0.6830170 0.6584525
[31] 1.2877883 1.1185829 1.0685545 0.9041312 0.8199964 0.9692281 0.6990717 0.7157646 0.5164071 0.4327213

$iterations
[1] 18  0

$Lagrangian
 [1] 0.000000000 0.017555148 0.000000000 0.000000000 0.000000000 0.000000000 0.003170138 0.053523534
 [9] 0.196488559 0.000000000 0.000000000 0.000000000 0.000000000 0.094706353 0.000000000 0.005788359
[17] 0.000000000 0.038446317 0.000000000 0.069813443 0.045252374 0.000000000 0.029404307 0.005898483
[25] 0.000000000 0.045048638 0.010242070 0.000000000 0.000000000 0.000000000 0.000000000 0.074615838
[33] 0.000000000 0.008346482 0.000000000 0.000000000 0.000000000 0.008633070 0.065916062 0.000000000
[41] 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000
[49] 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000
[57] 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000
[65] 0.000000000 0.000000000

$iact
 [1]  9 14 32 39 20 26  8 18 21 23  2 34 27 16 38 24  7

それをプロット(ばらつきを入れる前のデータと入れた後のデータのそれぞれについて、推測グラフと実測値グラフ)

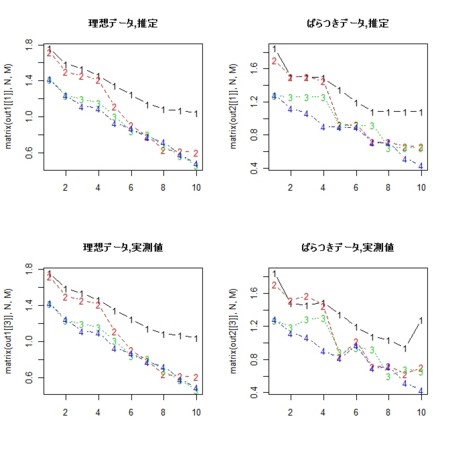
par(mfcol=c(2,2))

matplot(matrix(out1[[1]],N,M),type="b",main="理想データ,推定")
matplot(matrix(out1[[3]],N,M),type="b",main="理想データ,実測値")

matplot(matrix(out2[[1]],N,M),type="b",main="ばらつきデータ,推定")

matplot(matrix(out2[[3]],N,M),type="b",main="ばらつきデータ,実測値")

par(mfcol=c(1,1))

推定結果と実測値をプロットする

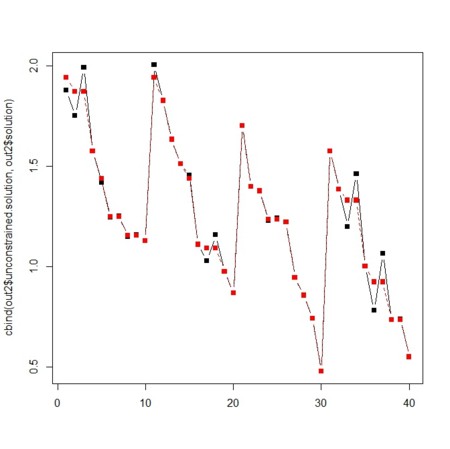
matplot(cbind(out1$unconstrained.solution,out1$solution),type="b",pch=15,col=c(rep(1:M,2)))
matplot(cbind(out2$unconstrained.solution,out2$solution),type="b",pch=15,col=c(rep(1:M,2)))