情報を利用する ２

• こちらの続き
• 積分を関数にして、どのような男女比での観察が、尤度比をどのように変えるかを見てみる

Aimai<-function(Nm,Nf){# 男女の観察人数
	N<-Nm+Nf # 男女総数
	# 男女の事後確率を男女２仮説に共通の係数部分を省略した関数
	integrandM <- function(x) {
		exp(2*Nm*log(x)+2*Nf*log(1-x)) + exp(N*(log(x)+log(1-x)))
	}
	integrandF <- function(x) {
	  exp(2*Nf*log(x)+2*Nm*log(1-x)) + exp(N*(log(x)+log(1-x)))
	}
	# 積分する
	lower<-0.5
	upper<-1
	intM<-integrate(integrandM, lower = lower, upper = upper)
	intF<-integrate(integrandF, lower = lower, upper = upper)
	# 比とフラクションを計算
	RatioMF<-intM$value/intF$value
	sumIntMF<-sum(intM$value,intF$value)
	FracM<-intM$value/sumIntMF
	FracF<-intF$value/sumIntMF
	list(RatioMF=RatioMF,Fraction=c(FracM,FracF),int.m=intM,int.f=intF)
}

Aimai(Nm,Nf)

# 総人数を振って、その男女観察の内訳も振ってデータを取る
Ns<-seq(1:100)

outRatio<-matrix(1,length(Ns),max(Ns)+1)
outCol<-outFrac<-matrix(0,length(Ns),max(Ns)+1)
for(i in 1:length(Ns)){
	Nms<-0:Ns[i]
	for(j in 1:length(Nms)){
		Nm<-Nms[j]
		Nf<-Ns[i]-Nm
		out.aimai<-Aimai(Nm,Nf)
		outRatio[i,j]<-out.aimai$RatioMF
		outFrac[i,j]<-out.aimai$Fraction[1]
		outCol[i,j]<-1
		if(Nm/Ns[i]==0.6)outCol[i,j]<-2
	}
}
image(log(outRatio))
persp(log(outRatio))
library(rgl)

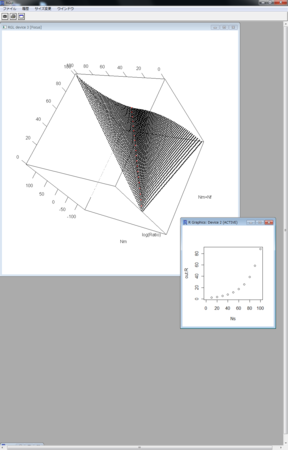
plot3d(row(outRatio),col(outRatio),log(c(outRatio)),col=outCol,xlab="Nm+Nf",ylab="Nm",zlab="log(Ratio)")
image(log(outFrac))

# 特定の男女観察人数比について、総人数を振ってデータを取る
Nms<-6*(1:10)
Nfs<-4*(1:10)
Ns<-Nms+Nfs

out.R<-out.F<-rep(0,length(Nms))
for(i in 1:length(Nms)){
	tmpout<-Aimai(Nms[i],Nfs[i])
	out.R[i]<-tmpout$RatioMF
	out.F[i]<-tmpout$Fraction[1]
}

plot(Ns,out.R,xlim=c(0,max(Ns)))