数学・コンピュータ関連の姉妹ブログ『ryamadaのコンピュータ・数学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

第２章　Erdos-Renyi ランダムグラフ　ぱらぱらめくる『ランダム グラフ ダイナミクス』

グラフ 確率 ぱらぱらめくるシリーズ
  • Erdos-Renyi ランダムグラフを作ってみる
    • ランダムグラフはエッジがあるかないかを確率的に決めることでできる
    • その確率を増やしていくと、急に、大きな連結成分ができる

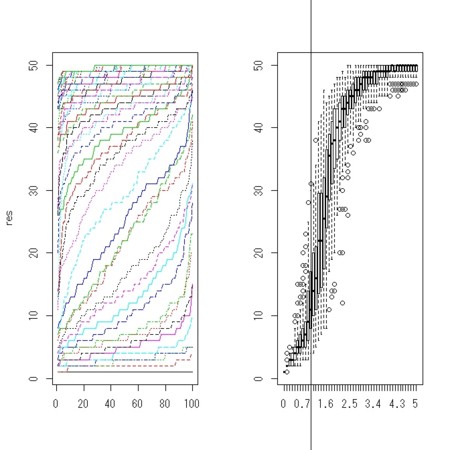
    • Erdos-Renyiランダムグラフとはどんなものか、を知るにはべたべたとソースを書いてみるのがよいが、igraphパッケージには関数erdos.renyi.game()があるらしい
library(igraph)


Nv <- 50

E.m <- matrix(0,Nv,Nv)

lambdas <- seq(from=0,to=5,length=51)
n.iter <- 100
res <- matrix(0,length(lambdas),n.iter)
for(i in 1:length(lambdas)){
	lambda <- lambdas[i]
	p <- lambda/Nv
	for(j in 1:n.iter){
		E.m[which(upper.tri(E.m))] <- sample(c(0,1),length(which(upper.tri(E.m))),replace=TRUE,prob= c(1-p,p))

		#E.m <- E.m + t(E.m)
		g <- graph.adjacency(E.m,mode = "undirected")
		#print(sum(E.m)/(Nv^2))
		#plot(g, layout=layout.kamada.kawai, vertex.color="green")
		#plot(g, layout=layout.circle, vertex.color="green")

		decomp <- decompose.graph(g)
		tmp <- rep(0,length(decomp))
		for(k in 1:length(tmp)){
			tmp[k] <- decomp[[k]][[1]]
		}
		res[i,j] <- max(tmp)
		#str(decomp)
	}
	
}

res <- apply(res,1,sort)
par(mfcol=c(1,2))
matplot(res,type="l")

boxplot(res,names = factor(lambdas))
abline(v = which(lambdas == 1))
par(mfcol=c(1,1))

    • マルチンゲール
      • この例では、平均子供数\muがあるとき、世代における子孫数Z_tの期待値は\mu^tとなっている
      • Z_tの期待値は\muの関数でわかるが、何人の子孫がいる確率がいくつなのかは、これだけではわからない。何人の子孫か、の確率Z_tについて\frac{Z_t}{\mu^t}が変わらないことが示せるが、このようなとき\frac{Z_t}{\mu^t}はマルチンゲールだ、と言う
      • それを確認してみよう(横軸が世代、縦軸が子供の数の期待値を\mu^tで割った値)

      • マルチンゲールなら必ず(有限な極限に)収束するという事実を用いると、\mu = 1であって、それが「確率1で子供の数が1である」という場合を除いて、0に収束する(ことも数学的に示せる)
      • \mu > 0のときの\frac{Z_t}{\mu^t}の期待値は\mu^tだが、子供の数は多かったり少なかったりして、子供が何人の確率がいくつに収束するかは別問題。その子供の数別の収束値が0でないための条件も数学的に示せる
      • 期待値が0以外に収束する、とは、絶滅もするけれど、絶滅しない確率も一定程度あることを意味する。その絶滅しない場合はどうなるの？ということにも興味がある
      • 絶滅しない場合に興味があるなら、絶滅する場合にも興味があって、その場合の子孫数の分布はポアッソン分布
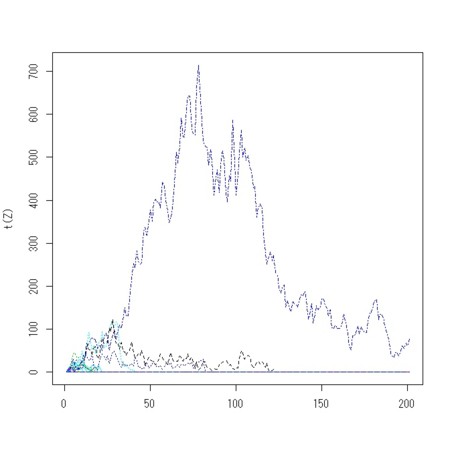
    • 子孫数の変化を追いかけて示すソース
# 追加世代数
max.t <- 200
library(MCMCpack)
# １個体あたりの最大子供数
max.offspring <- 6
# 子供の数の期待値が１前後で「増え続けたり」「絶滅」したりするので、それをうまく調整した、子供の数の確率
# 「期待値」が重要であることを示すためにてんでんばらばらにする
P <- rep(0,max.offspring+1)
P[2:max.offspring] <- rdirichlet(1,rep(1,max.offspring-1))*runif(1)/max.offspring
# 期待値が１から少し増える(か減るかさせる)
delta <- -0.00001
P[max.offspring+1] <- (1-sum((0:max.offspring)*P))/max.offspring+delta
P[1] <- 1- sum(P)
# 確率の和が１であることの確認
sum(P)
# 期待値が１近傍であることの確認
sum((0:max.offspring) * P)
# シミュレーション回数
n.iter <- 100
Z <- matrix(0,n.iter,max.t+1)
# 時刻0では個体数は１
Z[,1] <- 1
for(j in 1:n.iter){
	for(i in 2:(max.t+1)){
		if(Z[j,i-1] == 0){
			Z[j,i] <- 0
		}else{
			Z[j,i] <- sum(sample(0:max.offspring,Z[j,i-1],replace =TRUE, prob=P))
			
		}
	}
}

matplot(t(Z),type="l")
    • 期待値を\mu^tで割ったものが一定であることを示すソース
max.t <- 20
library(MCMCpack)
max.offspring <- 6

P <- rep(0,max.offspring+1)
P[2:max.offspring] <- rdirichlet(1,rep(1,max.offspring-1))*runif(1)/max.offspring
delta <- +0.01
P[max.offspring+1] <- (1-sum((0:max.offspring)*P))/max.offspring+delta
P[1] <- 1- sum(P)
sum(P)
mu <- sum((0:max.offspring) * P)
mu
n.iter <- 10000
Z <- matrix(0,n.iter,max.t+1)
Z[,1] <- 1

for(j in 1:n.iter){
	for(i in 2:(max.t+1)){
		if(Z[j,i-1] == 0){
			Z[j,i] <- 0
		}else{
			Z[j,i] <- sum(sample(0:max.offspring,Z[j,i-1],replace =TRUE, prob=P))
			
		}
	}
}

matplot(t(Z),type="l")

mean.Z <- apply(Z,2,mean)
plot(mean.Z)

plot(mean.Z/(mu^(0:max.t)),ylim = c(0,2))
    • 子供数が何人の比率が安定することを示すソース
# 追加世代数
max.t <- 100
library(MCMCpack)
# １個体あたりの最大子供数
max.offspring <- 10
# 子供の数の期待値が１前後で「増え続けたり」「絶滅」したりするので、それをうまく調整した、子供の数の確率
# 「期待値」が重要であることを示すためにてんでんばらばらにする
P <- rep(0,max.offspring+1)
P[2:max.offspring] <- rdirichlet(1,rep(1,max.offspring-1))*runif(1)/max.offspring
# 期待値が１から少し増える(か減るかさせる)
delta <- 0.001
P[max.offspring+1] <- (1-sum((0:max.offspring)*P))/max.offspring+delta
P[1] <- 1- sum(P)
# 確率の和が１であることの確認
sum(P)
# 期待値が１近傍であることの確認
sum((0:max.offspring) * P)
# シミュレーション回数
n.iter <- 10000
Z <- matrix(0,n.iter,max.t+1)
# 時刻0では個体数は１
Z[,1] <- 1
for(j in 1:n.iter){
	for(i in 2:(max.t+1)){
		if(Z[j,i-1] == 0){
			Z[j,i] <- 0
		}else{
			Z[j,i] <- sum(sample(0:max.offspring,Z[j,i-1],replace =TRUE, prob=P))
			
		}
	}
}

Z.tab <- apply(Z,2,tabulate,nbins =max(Z))

matplot(t(Z.tab)/n.iter,type="l",ylim = c(0,0.01))
# 絶滅しない場合の内訳は…
matplot(t(Z.tab)/(n.iter-Z.tab[1,]),type="l",ylim = c(0,0.01))
  • 感染症としてのクラスター成長
    • 個人が免疫なし、感染中(伝染力あり)、免疫ありの３状態を取りえるような状況で、個人間の接触をランダムグラフのノード間のエッジに見立てる話
    • 子孫繁栄の条件と違うのは、限定された人口中に「自分の仲間」を広げて行く点。分枝で必ずしも子孫が増えない(バッティングする)ことによる項が入る点。
    • ただし、人口が十分に大きいときは、分枝モデルで近似できる
    • もしくは、分枝の項から必ずしも増やせないことがある項を差し引いたものは分枝モデルになっている、とも言い換えられる
n <- 500
max.t <- 100
time <- 1:max.t

Status <- matrix(0,max.t,n)
Status[1,1] <- 1
lambda <- 1.01
p <- lambda/n
for(i in 2:max.t){
	E.m <- matrix(0,n,n)
	E.m[which(upper.tri(E.m))] <- sample(c(0,1),length(which(upper.tri(E.m))),replace=TRUE,prob= c(1-p,p))
	E.m <- E.m + t(E.m)
	infs <- which(Status[i-1,]==1)
	suss <- which(Status[i-1,]==0)
	if(length(infs) ==0 || length(suss) == 0){break}
	I.E.m <- matrix(E.m[infs,suss],nrow=length(infs))
	print(dim(I.E.m))
	infection <- sign(apply(I.E.m,2,sum))
	print(infection)
	Status[i,] <- Status[i-1,]
	Status[i,infs] <- 2
	Status[i,suss[which(infection==1)]] <- 1
}
Loc <- matrix(runif(n*2),ncol=2)
for(i in 1:max.t){
	title <- paste("",i)
	plot(Loc,col = Status[i,]+1,pch=20,cex=2,main = title)
	Sys.sleep(0.1)
	if(sum(dist(Status[i,]))==0){
		break
	}
}
#matplot(Status,type="l")
  • ランダムウォークとしてのクラスター成長
    • 分枝過程は数学的に扱えるモデル
    • ランダムウォークも数学的に扱えるモデル
    • ランダムウォークの方が展開しやすい(単純だから…)
    • ということで、ランダムウォークを使ってモデルを作れるとよいが…
    • 変化を追跡したいのがクラスターサイズとすると、クラスターサイズという変数が確率的に変化するように作るのがよい
    • 感染中と免疫なしとのそれぞれの個体数に応じて決まる増分と、それより少し少なめにしたい分とを変化量とする
    • いったんランダムウォークのパラメタが決まれば、そのランダムウォークの特性を検討することが数学的な問題となる
    • 増分とモーメント母関数
      • 増分はクラスターサイズが1,2,...,と無限の場合のそれぞれについて考える必要がある(長さが無限大のベクトルで考える)。無限のものは扱いにくいので、モーメント母関数を用いて、「係数」の列が無限ベクトルに対応するようにすると、数学的に扱いやすくなるので、それを使っている
    • 既存の分布で考える
      • 量が分布するとき、特性がわかっている確率分布の話・組合せに持ち込むことは便利なので、随所にそのような記述が出る
    • 伝染が広がる条件においては、その条件によって定まるある値があって、その値より大きい連結成分がただ一つ、必ず(漸近的に確率１で)できる、というようなことを示すこともできる。Large deviations theory などもそれを示す過程で使う
      • このようにしてできる連結成分は巨大となりえて、それを巨大連結成分と呼ぶ
    • ランダムな仮定の全体に関して何かを知るというのではなく、「起きる特定のこと」に絞って、その何かを知りたい、という話の例にもなっている
  • 巨大連結成分
    • 巨大連結成分の何が知りたいか、そして何は(数学的に)知りえるか
      • 直径
      • 最短距離分布
  • グラフの複雑度
    • 木(複雑度0)、単一サイクルグラフ(複雑度1)、複雑度2...
    • せいぜい複雑度は1まで、それ以上複雑なグラフはめったにできないことが示せる
  • 次数の分布
    • ポアッソン分布

logo

図書室

日記全体の目次
(記事一覧)

疾患遺伝子解析を学ぶためのカタログ(H18 3月改訂)の目次

 教科書

京都大学大学院医学研究科集中講義 全８限Part I(2007)
京都大学大学院医学研究科集中講義 全８限Part II(2008)
京都大学大学院医学研究科統計遺伝学講義 全８限(2009)

以下の関連サイトへのリンク道案内ページ
遺伝子多型解析Wiki
東大医科研HGCゲノム機能解析分野(旧)
理研リウマチチーム解析資料ページ


疾患遺伝子解析を学ぶためのカタログ(H18 3月改訂)
遺伝統計学のための統計学基礎 全９限
Haploviewを用いた連鎖不平衡マッピング解析実習 全９限
Arlequinを用いた集団遺伝学実習 全７限
一から始める遺伝子多型・形質関連解析
多数のGWAS/GWASメタアナリシスとその周辺解析用のアプリケーションへのリンク

複合遺伝性疾患とは

----------News----------
20万アクセス
2008/07/20
40万アクセス
2010/09/12


-------------------------