2012-08-09

染色体グラフ

こちらで、ランダムグラフを勉強している
Y染色体の伝搬をランダムグラフで扱ったり、巨大な連結グラフに確率過程を持ち込むことで、数学的に扱って、グラフの特徴を定性的・定量的に求める考え方が書かれている
染色体の伝搬をY染色体のように単純に考えずに組換えありで扱うと、どんな風になるか(扱えるのかも含めて)、夏休みらしく、うまく行かなくても、いいか、というスタンスでやってみることにする
変数設定
- グラフの構成成分
  - ノードは、すべての塩基とする
  - エッジは、染色体上のつながりと、親子関係の伝達との２種類とする
- ノードの属性
  - ノードは座標を持つ
    - 染色体をこの世という空間にある点とみなしたときの、その位置座標
    - 染色体上の塩基番号という座標
      - 染色体には、必ず交叉が起きるというルールがあるので、染色体に必ず交叉を入れるような設定にして、染色体間の距離は、そのような交叉発生のルールのもとで、ほぼ0.5の確率で奇数回の交叉が入るようなものを取ればよさそうだ
    - 時刻という座標
- エッジの属性
  - 染色体というつながりか、伝達というつながりか、の２種類に分かれる
そうは言っても
- まず、染色体のグラフを作って、その上で、塩基のノードとそれらの関連にエッジをつけるのが手順としてはよさそうだ
まずはイザナギ・イザナミ(アダムとイブ)からスタートにしよう
- 世代ごとに少しずつ人口をふやしつつ
- ペアリングに制約を入れることを考慮し
- 移住しながら…

# 第１世代は2人
init.n <- 2
# 世代数
n.gen <- 50
# 世代別人口
pop.gen <- c(init.n)
# 空間座標
loc <- list()
loc[[1]] <- matrix(0,pop.gen[1],2)
loc[[1]] <- loc[[1]] + rnorm(length(loc[[1]]))
# 親情報
parents <- list()
parents[[1]] <- matrix(0,pop.gen[1],2)
# 空間的に近すぎる個人ペアはペアリング不可
thres = 0 # 0とは「同一個人を両親とするのは不可」の意味
# 世代ごとの人口増加率
incr.ratio <- 1.05
# 移住パラメタ
migration <- runif(2)

for(i in 2:n.gen){
	# ペアリングは近い方がペアになり易い
	d <- matrix(0,pop.gen[i-1],pop.gen[i-1])
	for(j in 1:(pop.gen[i-1]-1)){
		for(j2 in (j+1):pop.gen[i-1]){
			d[j,j2] <- d[j2,j] <- sum((loc[[i-1]][j,]-loc[[i-1]][j2,])^2)
		}
	}
	d[which(d <= thres)] <- Inf
	prob <- exp(-d^2/2)
	prob <- prob/sum(prob)
	# 次世代人口の最大値
	max.child <- pop.gen[i-1]*incr.ratio * 5
	# 子供数は、2から最大値まで(絶滅しない設定)
	n.child <- sample(2:max.child,1,prob = dpois(2:max.child,pop.gen[i-1]*incr.ratio))
	pop.gen <- c(pop.gen, n.child)
	#print(pop.gen)
	parents.number <- sample(1:length(d),pop.gen[i],replace=TRUE,prob = prob)
	address <- matrix(1:length(d),pop.gen[i-1],pop.gen[i-1])
	parents.list <- which(address <= max(address),arr.ind=TRUE)
	parents[[i]] <- parents.list[parents.number,]
	#print(parents[[i]])
	loc[[i]] <- (loc[[i-1]][parents[[i]][,1],] + loc[[i-1]][parents[[i]][,2],])/2
	loc[[i]] <- loc[[i]] + cbind(rnorm(length(loc[[i]][,1]),rnorm(1,migration[1])),rnorm(length(loc[[i]][,2]),rnorm(1,migration[2])))
}

xlim <- ylim <- range(unlist(loc))
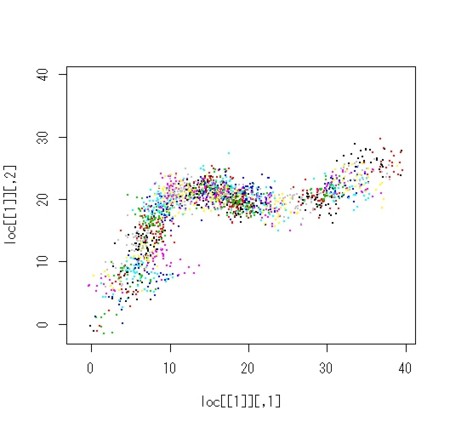
plot(loc[[1]],xlim = xlim, ylim = ylim,col=1,cex = 0.5,pch =20)
for(i in 2:n.gen){
	#plot(loc[[i]],xlim = xlim,ylim=ylim)
	points(loc[[i]],col=i,cex = 0.5,pch=20)
	Sys.sleep(0.1)
}

少し遊んでみる

library(MCMCpack)
# 第１世代は2人
init.n <- 10
# 世代数
n.gen <- 100
# 世代別人口
pop.gen <- c(init.n)
# 空間座標
loc <- list()
loc[[1]] <- matrix(0,pop.gen[1],2)
loc[[1]] <- loc[[1]] + rnorm(length(loc[[1]]),sd=1)
#loc[[1]] <- loc[[1]] + rdirichlet(init.n,rep(1,2))*10
#loc[[1]] <- loc[[1]] - 0.5
# 親情報
parents <- list()
parents[[1]] <- matrix(0,pop.gen[1],2)
# 空間的に近すぎる個人ペアはペアリング不可
#thres = 0 # 0とは「同一個人を両親とするのは不可」の意味
thres = mean(abs((c(loc[[1]])))) # 0とは「同一個人を両親とするのは不可」の意味
# 世代ごとの人口増加率
incr.ratio <- 1.01
# 移住パラメタ
migration <- runif(2)

for(i in 2:n.gen){
	# ペアリングは近い方がペアになり易い
	d <- matrix(0,pop.gen[i-1],pop.gen[i-1])
	for(j in 1:(pop.gen[i-1]-1)){
		for(j2 in (j+1):pop.gen[i-1]){
			d[j,j2] <- d[j2,j] <- sum((loc[[i-1]][j,]-loc[[i-1]][j2,])^2)
		}
	}
	print(length(which(d <= thres)))
	d[which(d <= thres)] <- 1/d[which(d <= thres)]
	prob <- exp(-d^2/2)
	prob <- prob/sum(prob)
	# 次世代人口の最大値
	max.child <- pop.gen[i-1]*incr.ratio * 5
	# 子供数は、2から最大値まで(絶滅しない設定)
	n.child <- sample(2:max.child,1,prob = dpois(2:max.child,pop.gen[i-1]*incr.ratio))
	pop.gen <- c(pop.gen, n.child)
	#print(pop.gen)
	parents.number <- sample(1:length(d),pop.gen[i],replace=TRUE,prob = prob)
	address <- matrix(1:length(d),pop.gen[i-1],pop.gen[i-1])
	parents.list <- which(address <= max(address),arr.ind=TRUE)
	parents[[i]] <- parents.list[parents.number,]
	#print(parents[[i]])
	loc[[i]] <- (loc[[i-1]][parents[[i]][,1],] + loc[[i-1]][parents[[i]][,2],])/2
	loc[[i]] <- loc[[i]] + cbind(sign(loc[[i]][,1])*rnorm(length(loc[[i]][,1]),rnorm(1,migration[1])),sign(loc[[i]][,2])*rnorm(length(loc[[i]][,2]),rnorm(1,migration[2])))
	loc[[i]] <- loc[[i]] + cbind((loc[[i]][,2]),-(loc[[i]][,1])) /mean(abs(loc[[i]]))
}

xlim <- ylim <- range(unlist(loc))
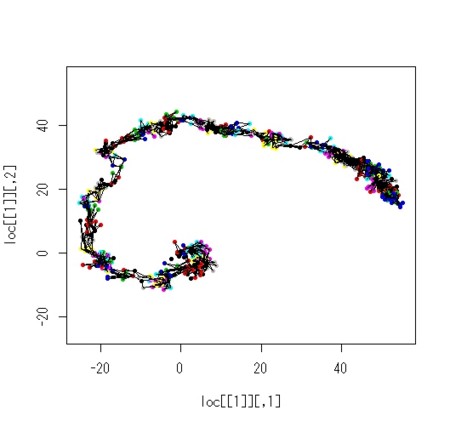
plot(loc[[1]],xlim = xlim, ylim = ylim,col=1,cex = 1,pch =20)
for(i in 2:n.gen){
	#plot(loc[[i]],xlim = xlim,ylim=ylim)
	points(loc[[i]],col=i,cex = 1,pch=20)
	for(j in 1:pop.gen[i]){
		segments(loc[[i]][j,1],loc[[i]][j,2],loc[[i-1]][parents[[i]][j,1],1],loc[[i-1]][parents[[i]][j,1],2])
		segments(loc[[i]][j,1],loc[[i]][j,2],loc[[i-1]][parents[[i]][j,2],1],loc[[i-1]][parents[[i]][j,2],2])
		Sys.sleep(0.01)
	}
	Sys.sleep(0.1)
}