エントロピーベースで分布の差異の関連検定

• 昨日のさらに続き
• このやり方で本当にいいかは未確定
• 0/1の説明変数があるとする
• 目的変数は２次元の点座標のデータ
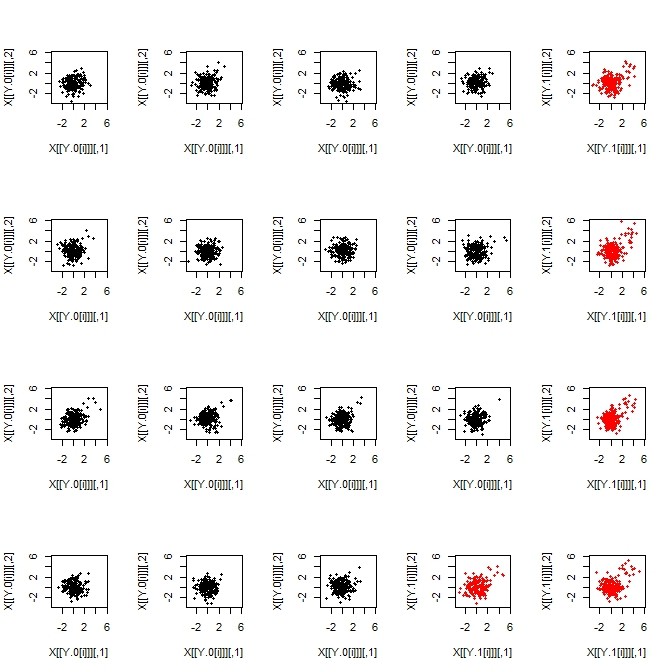
• 目的変数を20標本分プロットした。説明変数の２群を黒点プロットと赤点プロットで分けた
  • このプロットの心：原点を中心に２次元正規分布するのが基本であって、それぞれわずかな画分が右上斜めに移動する。ただし黒点群と赤点群とでは、右斜め上移動数に差がある

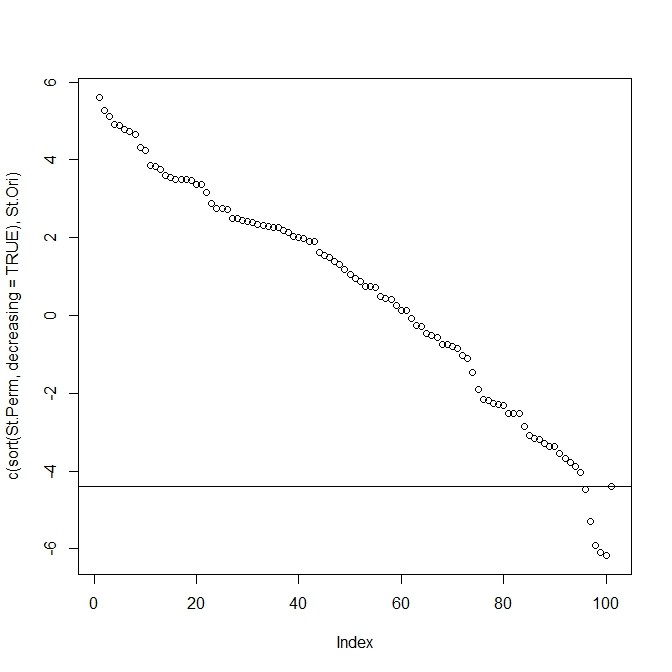
• これを、標本間のKLdivergenceで評価して、「群内KLdivergence総和」の多寡でパーミュテーションp値化してみよう
• たったの２０検体。p値は0.05くらいになった
• プロットからの印象で黒・赤別で分布に差があると感じる強さと比較的うまく行っているp値なのでは…

n <- 20
X <- list()
Y <- sample(0:1,n,replace=TRUE,prob=c(0.7,0.3))
N <- 200
d <- 2
for(i in 1:n){
	X[[i]] <- matrix(rnorm(N*d),ncol=d)
	n.s <- sample(0:5,1)
	if(Y[i]==1){
		#if(runif(1) < 0.5){
			n.s <- sample(10:20,1)
		#}
	}
	if(n.s>0){
		X[[i]][1:n.s,1:2] <- matrix(rnorm(n.s*2,3),ncol=2)
	}
	
	
}

KL.D <- matrix(0,n,n)

for(i in 1:n){
	for(j in 1:n){
		KL.D[i,j] <- KL.divergence(X[[i]],X[[j]])[1]
	}
}
diag(KL.D) <- 0
Y.0 <- which(Y==0)
Y.1 <- which(Y==1)
tmp.0 <- tmp.1 <- 0
xlim <- ylim <- range(unlist(X))
par(mfcol=c(4,5))
for(i in 1:length(Y.0)){
	tmp.0 <- tmp.0 + sum(KL.D[Y.0[i],Y.0])
	plot(X[[Y.0[i]]],xlim=xlim,ylim=ylim,pch=20)
}
for(i in 1:length(Y.1)){
	tmp.1 <- tmp.1 + sum(KL.D[Y.1[i],Y.1])
	plot(X[[Y.1[i]]],xlim=xlim,ylim=ylim,pch=20,col=2)
}

St.Ori <- tmp.0 + tmp.1
n.iter <- 100
St.Perm <- rep(0,n.iter)
for(j in 1:n.iter){
	tmp.Y.1 <- sample(1:n,sum(Y))
	tmp.Y.0 <- (1:n)[-tmp.Y.1]
	tmp.0 <- tmp.1 <- 0
	for(i in 1:length(tmp.Y.0)){
		tmp.0 <- tmp.0 + sum(KL.D[tmp.Y.0[i],tmp.Y.0])
	}
	for(i in 1:length(tmp.Y.1)){
		tmp.1 <- tmp.1 + sum(KL.D[tmp.Y.1[i],tmp.Y.1])
	}

	St.Perm[j] <- tmp.0 + tmp.1

}

plot(c(sort(St.Perm,decreasing=TRUE),St.Ori))
abline(h=St.Ori)