２ 複数候補の好悪順序にルールを入れる

• 前の記事からの続き
• 複数の候補はある尺度に関して順序をつけることができるとする
• そして選挙権者は候補者に対する好悪の程度がこの尺度上での距離によって決まるものとする
• このとき、どんな変化になるだろうか
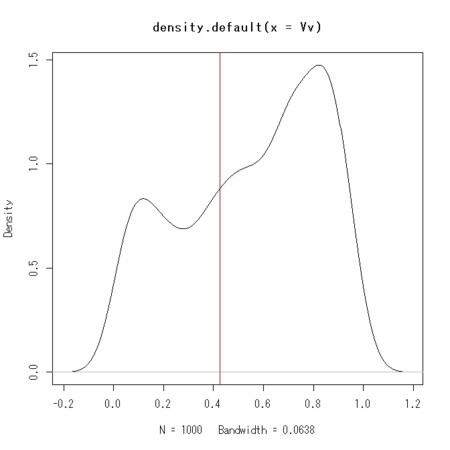
• 選挙権者の意見の分布を描き、当選者の意見の位置を赤で示した

• こちらに続く

# 投票
# 選挙権者数
Nv <- 1000
# 候補者数
Nc <- 100
# 候補者の主張の値を与える
# 候補者の主張をばらつかせながら偏らせる
Cv <- c(rbeta(Nc/2,1,3), rbeta(Nc/2,10,1))
# 選挙権者の主張も値化する
# 主張値を１峰性でないようにする
Vv <- c(rbeta(Nv/2,1,2),rbeta(Nv/2,6,2))
# Nv人の好き嫌い順を描き出した行列を作る
# 選挙権者と候補者の主張値の差の絶対値は好き嫌いを非負実数で表す
Opinions <- abs(outer(Vv,Cv,FUN="-"))
Opinions <- Opinions / max(Opinions)
Opinions <- 1-Opinions
# １人ずつ候補者を減らしていく過程が以下
loop <- TRUE
# 初めは全員が投票対象
list.c <- 1:Nc
# ログを取ろう
log <- NULL
while(loop){
# 投票対象者をプリントアウト
	print("candidates")
	print(list.c)
# 選挙権者ごとに何番目の候補者に投票するかを確認
	votes <- t(apply(Opinions[,list.c],1,order))[,length(list.c)]
# 人数を集計して、その結果をプリントアウト
	res <- tabulate(votes,length(list.c))
	print("result")
	print(res)
	tmp <- rep(0,Nc)
	tmp[list.c] <- res
	log <- rbind(log, tmp)
# 過半数得票者がいるかどうかを確認
	if(max(res) > sum(res)/2){
# 過半数得票者がいれば、ループは止めて、被選出者を登録
		loop <- FALSE
		selected <- list.c[which(res == max(res))]
# 過半数得票者がいなければ
	}else{
# リストから外される候補者を選んで、外す
		tobe.deleted <- which(res == min(res))
# いきなり複数がはずれると、過半数を取らなくても、候補者が１人に絞られたりするのでそれを回避する
		tobe.deleted.2 <- sample(tobe.deleted,1)
		list.c <- list.c[-tobe.deleted.2]
		if(length(list.c) == 1){
			loop <- FALSE
			selected <- list.c
		}
	}
}
# 選出者
print(selected)
# 得票数の推移
matplot(log,type="l")

# 全体の意見分布
plot(density(Vv))
abline(v = Cv[selected],col = 2)