2012-11-03

二項布か

二項分布検定 R

昨日の記事はポアソン分布
今日は二項分布
こちらでは正規分布へのあてはめをしている
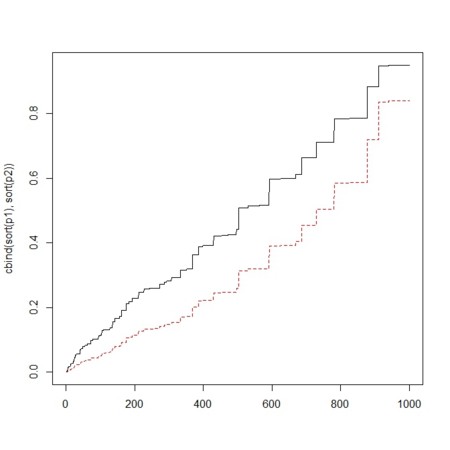
- 正規分布へのあてはめのときには、平均と分散との２パラメタを用いるので自由度の手加減のときに２を引く
二項分布のときは…１を引くようだ
期待値の小さいセルの合併は省略してあることに注意

n <- 10
m <- 8
p <- 0.5

n.iter <- 1000
X <- matrix(0,n.iter,n+1)
for(i in 1:n.iter){
	for(j in 1:m){
		s <- sample(0:1,n,replace=TRUE,prob=c(p,1-p))
		X[i,sum(s)+1] <- X[i,sum(s)+1] + 1
	}
}
X

Chisq <- rep(0,n.iter)
exp.X <- dbinom(0:n,n,p) * m
non.more.than.1 <- which(exp.X <= 1)
more.than.1 <- which(!(exp.X <= 1))
gappei.exp <- sum(exp.X[non.more.than.1])

for(i in 1:n.iter){
	Chisq[i] <- sum((c(X[i,more.than.1],sum(X[i,non.more.than.1]))-c(exp.X[more.than.1],gappei.exp))^2/c(exp.X[more.than.1],gappei.exp))
}

plot(sort(Chisq))
#plot(pchisq(sort(Chisq),length(more.than.1)+1-2,lower.tail=FALSE))
plot(sort(pchisq(Chisq,length(more.than.1)+1-1,lower.tail=FALSE)))

p1 <- pchisq(Chisq,length(more.than.1)+1-1,lower.tail=FALSE)
p2 <- pchisq(Chisq,length(more.than.1)+1-2,lower.tail=FALSE)

matplot(cbind(sort(p1),sort(p2)),type="l")

以降はこれを使ったちょっとした作業のメモ

# Simulate a sample data matrix X
Ms <- 400
G <- 1000
L <- sample(100:500,G,replace=TRUE)
mus <- rep(10,G)
X <- matrix(0,G,M+1)

for(i in 1:G){
	tmp.prob <- dpois(0:M,mus[i])
	#tmp.prob <- tmp.prob * (1+runif(M+1)*1)
	tmp.prob <- tmp.prob/sum(tmp.prob)
	tmp <- sample(0:M,L[i],replace=TRUE,prob = tmp.prob)
	#if(i == 1)tmp <- sample(0:M,L[i],replace=TRUE,prob = dpois(0:M,0.01))
	X[i,] <- c(length(which(tmp==0)),tabulate(tmp,nbins=M))
}

Y <- list()
# Summing-up the whole genes.
Yw <- list()
# ケース・コントロール
p<- 0.5
Y <- list()
ii <- 1
for(i in 1:G){
	Y[[i]] <- list()
	Y[[i]][[1]] <- X[i,1]
	Y[[i]][[1]] <- X[ii,1]
	for(j in 2:(M+1)){
		tmp <- sample(0:(j-1),X[i,j],replace=TRUE,prob = dbinom(0:(j-1),j-1,prob = p))
		tmp <- sample(0:(j-1),X[ii,j],replace=TRUE,prob = dbinom(0:(j-1),j-1,prob = p))
		Y[[i]][[j]] <- c(length(which(tmp==0)),tabulate(tmp,nbins=j-1))
	}
	if(i==1){
		Yw <- Y[[i]]
	}else{
		for(j in 1:(M+1)){
			Yw[[j]] <- Yw[[j]] + Y[[i]][[j]]
		}
	}
}

# Here, statistical calculation starts.

# Goodness of fit test

Lnull <- Lw <- Ls <- L.chisq <- p <- rep(0,G)
Lxw <- Lxs <- Lx.chisq <- px <- rep(0,G)
Chisq <- rep(0,G)
df2 <- 0
for(i in 1:G){
	tmp.chisq <- 0
	for(j in 1:length(Y[[i]])){
		#tmp.exp <- Yw[[j]]/sum(Yw[[j]]) * sum(Y[[i]][[j]])
		tmp.exp <- dbinom(0:(length(Y[[i]][[j]])-1),length(Y[[i]][[j]])-1,0.5)*sum(Y[[i]][[j]])
		more.than.1 <- which(!(tmp.exp <=1))
		not.more.than.1 <- which(tmp.exp <= 1)
		non.zero <- which(tmp.exp != 0) 
		if(i==1)df2 <- df2 + max(0,length(more.than.1)+1-1)
		#if(i==1)df2 <- df2 + max(0,length(more.than.1)+1-2)
		if(length(non.zero) > 1){
			tmp.chisq <- tmp.chisq + sum(((c(Y[[i]][[j]][more.than.1],sum(Y[[i]][[j]][not.more.than.1]))-c(tmp.exp[more.than.1],sum(tmp.exp[not.more.than.1])))^2)/(c(tmp.exp[more.than.1],sum(tmp.exp[not.more.than.1]))))

		}
	}
	Chisq[i] <- Chisq[i] + tmp.chisq
	for(j in 2:length(Y[[i]])){
		#print(Y[[i]][[j]])
		L.common <- lgamma(sum(Y[[i]][[j]])+1) -sum(lgamma(Y[[i]][[j]]+1))
		if(sum(Y[[i]][[j]]) !=0){
			tmp2 <- dbinom(0:(length(Y[[i]][[j]])-1),Y[[i]][[j]],prob = 0.5)
			tmp1 <- Y[[i]][[j]]/sum(Y[[i]][[j]])
			tmp3 <- Yw[[j]]/sum(Yw[[j]])
			tmp.p <- sum((0:(length(Y[[i]][[j]])-1)) * Yw[[j]])/(sum(Yw[[j]])*(length(Yw[[j]])-1))
			#print(tmp.p)
			if(tmp.p != 0){
				tmp4 <- dbinom(0:(length(Y[[i]][[j]])-1),sum(Y[[i]][[j]]),prob = tmp.p)
				non.zero <- which(tmp4!=0)
				Lw[i] <- Lw[i] + L.common + sum(Y[[i]][[j]][non.zero] * log(tmp4[non.zero]))
			}
			tmp.p1 <- sum((0:(length(Y[[i]][[j]])-1)) * Y[[i]][[j]])/(sum(Y[[i]][[j]])*(length(Y[[i]][[j]])-1))
			#print(tmp.p1)
			if(tmp.p1 !=0){
				tmp5 <- dbinom(0:(length(Y[[i]][[j]])-1),sum(Y[[i]][[j]]),prob = tmp.p1)
				non.zero <- which(tmp5!=0)
				Ls[i] <- Ls[i] + L.common + sum(Y[[i]][[j]][non.zero] * log(tmp5[non.zero]))

			}
			non.zero <- which(tmp2 != 0)
			Lnull[i] <- Lnull[i] + L.common + sum(Y[[i]][[j]][non.zero] * log(tmp2[non.zero]))
			non.zero <- which(tmp3 != 0)
			Lxw[i] <- Lxw[i] + L.common + sum(Y[[i]][[j]][non.zero] * log(tmp3[non.zero]))
			non.zero <- which(tmp1 != 0)
			Lxs[i] <- Lxs[i] + L.common + sum(Y[[i]][[j]][non.zero] * log(tmp1[non.zero]))
		}

	}
}
#df2 <- length(which(unlist(Yw)!=0))

P <- pchisq(Chisq,df2,lower.tail = FALSE)

par(mfcol=c(2,2))
plot(sort(Chisq))
plot(sort(P))
plot(L,Chisq)
plot(L,P)
par(mfcol=c(1,1))