コルモゴロフ=スミルノフ統計量その１(0に概収束する)

• まず、Rのks.test()関数の中身をぱくって、２標本の場合のks.test()統計量の算出のところだけを抜き出した関数を作っておこう

my.ks.stat <- function(x,y,type=c("less","greater","two.sided")){
	n.x <- length(x)
	n.y <- length(y)
	w <- c(x, y)
	z <- cumsum(ifelse(order(w) <= n.x, 1/n.x, -1/n.y))
	type <- match.arg(type)
	KS.stat <- switch(type, two.sided = max(abs(z)), greater = max(z), less = -min(z))
	KS.stat
}

• 同じ分布からの２標本(それぞれ値の個数をnとする)を作ってやる。同じ分布からだから、「帰無仮説」が成り立っている。この場合にks統計量がどういう値を取るかをシミュレーションしてみる
• 値の個数が大きくなるにつれ、0に近づくという(almost surely : a.s. : 概収束する(実は概収束の話は、こちらとか、それを受けてのこちらやこちらの話題)のだが、その様子を見るために、と変化させ、それぞれのnの値に対して、帰無仮説下での統計量をn.iter回出してみて、それを並べてプロットしてみよう

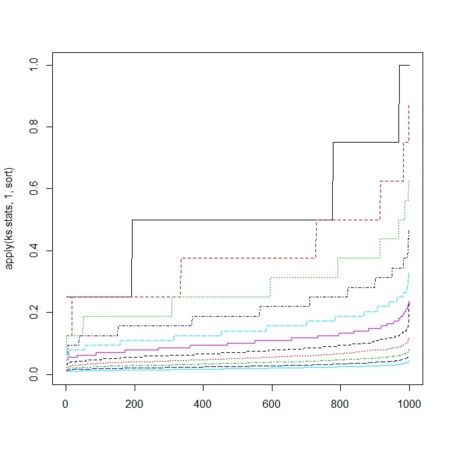
• • グラフは階段状である(nの値が有限だから)
  • だんだんグラフが下へ移動している(0に近くなっている)
  • nが大きくなると0に近づくというのは、ある値nでのks統計量の期待値が0に近づいている、ということ
  • ks統計量(の累積ぷrと)は、この図で示されるような「初めに0から立ち上がって、少し増加のペースが落ちて、その後、増加ペースが上がる」という形をしている

# 試行回数
n.iter <- 1000
# 値の数をだんだん増やす
ns <- 2^(2:12)
# 母集団の分布はきれいな分布関数でなくしたいので、次の値rを使って、正規分布と指数分布の混成としてみる
r = 0.3
# n.iter * length(ns) の行列にks統計量を納める
#ks.stats <- rep(NA,n.iter)
ks.stats <- matrix(NA,length(ns),n.iter)
for(i in 1:n.iter){
	for(j in seq(ns)){
		n <- ns[j]
		x <- x2 <- rep(NA,n)
		s <- sample(1:2,n,replace=TRUE,prob=c(r,1-r))
		s2 <- sample(1:2,n,replace=TRUE,prob=c(r,1-r))

		x.norm <- rnorm(n)
		x.exp <- rexp(n)
		x.norm2 <- rnorm(n)
		x.exp2 <- rexp(n)
		
		x[which(s==1)] <- x.norm[which(s==1)]
		x[which(s==2)] <- x.exp[which(s==2)]
		x2[which(s2==1)] <- x.norm2[which(s2==1)]
		x2[which(s2==2)] <- x.exp2[which(s2==2)]

		ks.stats[j,i] <- my.ks.stat(x,x2,type="two.sided")
	}
	

}

matplot(apply(ks.stats,1,sort),type="l")