ベルヌーイ分布の分散を推定する

• 前の記事では母分布が正規分布だった
• 母分布がベルヌーイ分布のときはどうなるだろうか
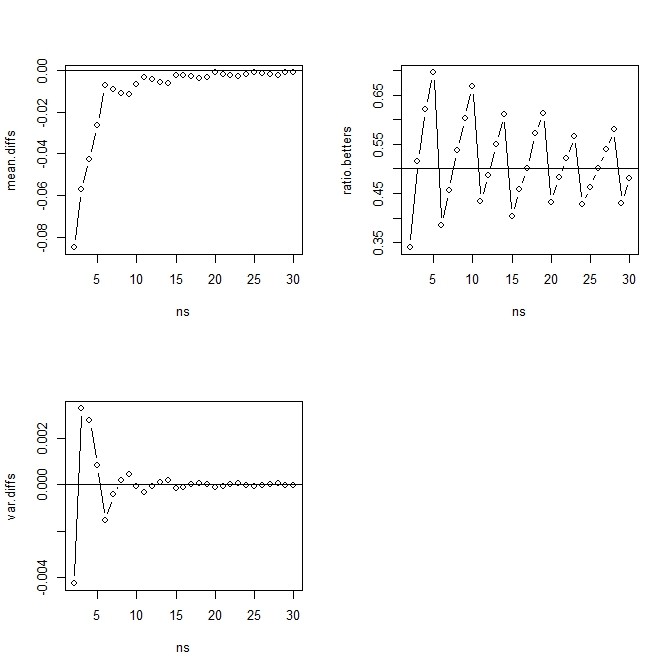
• ベルヌーイ分布の場合には、n数の影響が離散的に大きく効くので、n数を変化させながら、母分布の分散とのずれの平均値・分散、母分布の分散に近いのは２方法(標本分散と標本からの不偏分散)のうち標本分散の方が近い割合をプロットしてみる

m <- pi/4
s2 <- m*(1-m)
ns <- 2:30

mean.diffs <- var.diffs <- ratio.betters <- rep(0,length(ns))

for(nn in 1:length(ns)){
n <- ns[nn]
n.trial <- 10000
sample.mean <- sample.var <- sample.ub.var <- rep(0,n.trial)
for(i in 1:n.trial){
	X <- sample(0:1,n,replace=TRUE,prob=c(1-m,m))
	#X <- rnorm(n,m,sqrt(s2))
	sample.mean[i] <- mean(X)
	sample.var[i] <- sum((X-sample.mean[i])^2)/n
	sample.ub.var[i] <- var(X)
}
mean(sample.mean)
m
mean(sample.var)
mean(sample.ub.var)
s2
matplot(cbind(sort(sample.var),sort(sample.ub.var)),type="l",cex=0.1)
abline(h=s2)
diff.s.v <- abs(sample.var-s2)
diff.s.uv <- abs(sample.ub.var-s2)
mean(diff.s.v)
mean(diff.s.uv)
mean.diffs[nn] <- mean(diff.s.v)-mean(diff.s.uv)
var(diff.s.v)
var(diff.s.uv)
var.diffs[nn] <- var(diff.s.v)-var(diff.s.uv)

plot(diff.s.v,diff.s.uv)
abline(0,1,col=2)
abline(h=0,col=3)
abline(v=0,col=3)

ratio.betters[nn] <- length(which(diff.s.v<diff.s.uv)) / length(diff.s.v)
matplot(cbind(sort(diff.s.v),sort(diff.s.uv)),type="l",cex=0.1)
}

par(mfcol=c(2,2))
plot(ns,mean.diffs,type="b")
abline(h=0)
plot(ns,var.diffs,type="b")
abline(h=0)
plot(ns,ratio.betters,type="b")
abline(h=0.5)
par(mfcol=c(1,1))

• 正規分布のときと同じで、
• サンプリングを繰り返すと、標本平均のその平均は母分布の平均に近く、標本分散のその平均は母分布の分散からずれていて、標本から計算した不偏分散のその平均は母分布の分散に近いことが確かめられる
• サンプリングを繰り返せればよいけれど、一度の標本だったとしたら、標本分散と標本からの不偏分散とでは、どちらが母分布の分散に近いのだろう
  • 差の平均は標本分散の方が小さく、差の分散は周期的に変化する
• 標本分散と標本からの不偏分散とで母分散に近いのが標本分散である割合も周期的な変化をする

• 以下は一例(n=20の場合)

> mean(sample.mean)
[1] 0.78777
> m
[1] 0.7853982
> mean(sample.var)
[1] 0.1587795
> mean(sample.ub.var)
[1] 0.1671363
> s2
[1] 0.1685479

> mean(diff.s.v)
[1] 0.04212726
> mean(diff.s.uv)
[1] 0.0430174
> var(diff.s.v)
[1] 0.000993081
> var(diff.s.uv)
[1] 0.001112568

> length(which(diff.s.v<diff.s.uv)) / length(diff.s.v)
[1] 0.4252