第1章 確率、グラフ、因果モデル入門 ぱらぱらめくる『統計的因果推論』
- この章を読むときに:日頃から因果推論ばかりをやっている(臨床医とか)にはとっつきにくい文章かもしれない。「因果モデル」を中心に頭が回っているから。その場合は、「確率・統計」の部分は復習するつもりで読み、「因果」の部分は眼を閉じておいて、先に進む方が返ってよいかも…
- 確率、条件付き確率、事前確率、事後確率、事前オッズx尤度比=事後オッズ、確率変数、期待値、条件付き平均、分散、誤差最小と最良推定値、共分散、相関係数、条件付き相関係数、条件付き独立性、グラフォイド原理(対称性、分解性、弱結合性、縮約性、交差性)、連鎖講式(
)
- ノード、辺、隣接、有向グラフ、無向グラフ、連結、切断、非巡回的有向グラフ、親・子・子孫・先祖・配偶者、ルート、シンク、ツリーDAG、連鎖経路、完全、ベイジアンネットワーク
- ベイジアンネットワークはn個の
値確率変数が作る
個のセルを持つ表に同時確率を書き込む手間を省いたグラフ表現である
- 同時確率表現としてのネットワークに2種類
- 無向:マルコフネットワーク:対称かつ空間的な関係
- 有向DAG:ベイジアンネットワーク:因果的・時間的な関係
- その他(エッジが無向・有向の両方の場合があるもの、巡回ありの有向グラフ)
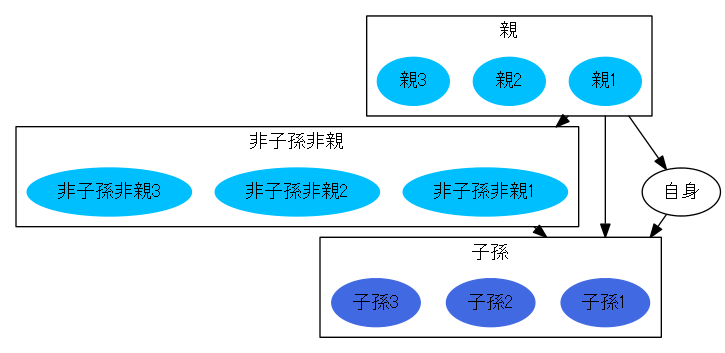
- DAGでは、あるノードに対して、「自身」「子孫」「非子孫」に分けられる
- 「子孫」は到達可能なノード
- 「非子孫」は到達不可能なノード
- 「非子孫」の亜集合である「親」
- 「親」は「非子孫」ノードの中で、上で言うところの「自身」に到達可能なノード
- 「非親である非子孫」は「非子孫」ノードの中で、上で言うところの「自身」に到達不可能なノード
、ただし
は
の親ノード集合
strict digraph G{
graph [compound=true];
graph [charset="UTF-8",fontname="MS UI Gothic"];
node[charset="UTF-8",fontname="MS UI Gothic"];
edge[charset="UTF-8",fontname="MS UI Gothic"];
subgraph cluster_sub_oya {
node [style=filled,color="#00BFFF"];
oya1 oya2 oya3;
label = "親";
}
subgraph cluster_sub_non_oya_non_sison {
node [style=filled,color="#00BFFF"];
nons1 nons2 nons3;
label = "非子孫非親";
}
subgraph cluster_sub_sison {
node [style=filled,color="#4169E1"];
c1 c2 c3;
label = "子孫";
}
oya1[label="親1"]
oya2[label="親2"]
oya3[label="親3"]
nons1[label="非子孫非親1"]
nons2[label="非子孫非親2"]
nons3[label="非子孫非親3"]
s[label="自身"]
c1[label="子孫1"]
c2[label="子孫2"]
c3[label="子孫3"]
oya1 -> s [ltail=cluster_sub_oya];
oya1 -> nons1 [ltail=cluster_sub_oya,lhead=cluster_sub_non_oya_non_sison];
oya1 -> c1 [ltail=cluster_sub_oya,lhead=cluster_sub_sison];
nons1 -> c1 [ltail=cluster_sub_non_oya_non_sison,lhead=cluster_sub_sison];
s -> c1 [lhead=cluster_sub_sison];
}dot -Kdot -Tpng ベイジアンネットワーク.txt -o ベイジアンネットワーク.png