ぱらぱらめくる『Nonparametric Regression』 - ryamadaの遺伝学・遺伝統計学メモ

資料はこちらの"Nonparametric Regression〜Appendix to An R an S-PLUS Comparison to Applied Regression"
1. Nonparametric Regression Models
- 一般型から始めよう
- k次元空間での回帰を考える
- パラメトリックな回帰モデルでは、 $y=f(\mathbf{\beta},\mathbf{x}=(x_1,...,x_k)$ という関数があると想定し、観察 $(\mathbf{x_i}=(x_{i1},...,x_{ik}),y_i)$ という組が $i=1,2,...,n$ 組あったときに、観察誤差を考慮して適切な $\mathbf{\beta}$ を推定しよう、という形である
- ノンパラにすると、 $\mathbf{\beta}$ の推定(これがパラメタ)はなくなる。その代わりに $\mathbf{x}$ という座標ごとに $y$ の値が何かしらのルールで推定できるようにしないといけない。 $y_i=f(\mathbf{x})$ の $f(.)$ がほしい。結局、関数を推定するわけでパラメトリックと変わりないようだが、関数がどんなものかは指定がないし、場所によって関数が違っていてもよいし(全体にわたる関数がないようなもの)、違うとみる
- このノンパラを１次元の $\mathbf{x}=(x_1)$ の場合に考えれば、散布図に「いい感じの(曲)線」を定める作業と同じ
- 多次元の場合に少し楽を仕様と思ったら $y=f(\mathbf{x})$ と考える代わりに、 $y=\alpha+\sum_{i=1}^k f_i(x_i)$ としてやることもできる。次元について単純な関数に制約していることになる。additive regression modelと呼ばれる
- 余談になるけれど、一般化線形回帰は、回帰のあてはめのところは線形回帰を使いつつ、それによって推定される値を引数とする関数によって $y$ を表させることでフレキシビリティを上げているが、additive regerssion modelから一般化線形回帰的に拡張することもできて、それによって、カバーできるモデルの範囲が広がるが、それは、何でもアリの一般型ほどには広くない
2. Estimation
- どうやってこれを実現するか
- 大きく２つの流れがあって、「近場の観察情報を使って」各所の推定をする方法(Local polynomial regressionが含まれる)と、「スムーズにする」ためにペナルティを入れる方法(スプライン関数推定)とに分けてもよさそうだ
- スプラインの方が関数の推定と言う意味でかっこいいが、多次元化するのが難しい面もあり、local polynomial regressionには捨てがたい面がある
- R(S)にはそのような関数がいくつもある
  - 「近場主義」
    - polynomial regression法:近場情報利用して、知りたい場所ごとに指定次の多項式近似を行う。lowess()とその一般次元化(？)したloess():Rでは基本関数
    - locfitパッケージのlocfit():(多分)polynomial regressionと同じように多項式近似を局所・近場で行うが、最適の選択において尤度を用いる
    - Generalized additive model: 前述の「次元ごとに局所多項式」をすることを原則とするが、それだとadditive regressionモデルに過ぎないので、そこに「一般化」を入れて、推定自体はadditive regressionだが、それをかぶせる関数を使って多様性を出している:mgcvパッケージのgam()
  - その他にもあるが…
  - 「スプライン関数」
    - smooth.spline():Rの基本セット
2'. やってみよう
- 一次元のデータ(折れ線もあったりする背景関数とその観測データ)

n <- 1000
t <- seq(from=-4,to=4,length=n)
y1 <- (1-t^2)*exp(-t^2/2)
plot(t,y1)
y2 <- abs((t-2)/3)
y3 <- 5/(t+5)
y4 <- y1-2*y2+y3
plot(t,y4,type="l")

x <- t+rnorm(length(t),0,0.1)
plot(x,y4)

Local Polynomial Regressionをlowess()で

# lowess
lowess.out <- lowess(x,y4,f=0.5,iter=0)
plot(x,y4)
lines(lowess.out,col=2)

- このlowess()は、(x,y4)から、任意のx軸上の真のy値を推定している。fは、あるxの値におけるyの値を推定するにあたって、xの左右に全レコード数のfの割合のレコードが含まれるような範囲を指定して、その値を使え、というパラメタ。iterは推定したあとに、その結果をチューニングする「やり直し」回数
- 推定にあたっては、fで選んだ範囲のxの幅が2hだったとして、その範囲のレコードになる重みをつけて、p次多項式近似をする、というルールになっている。重みづけ関数はこのtricube関数であってもほかの何かであってもよいのだが、lowess()では重みづけ関数を選ばせるオプションが無いようなので、このtribcube関数が使われているものと思われる。また、p次多項式を使うのがLocal Polynomial Regressionだが、この次数の指定方法もないので、p=1なのかと思われる
  - このtricube関数はこんなもの

t <- seq(from=-2,to=2,length=1000)
z <- rep(0,length(t))
s <- which(abs(t)<1)
z[s] <- (1-abs(t[s])^3)^3
plot(t,z,type="l")

- 実際、lowess()の一般次元化関数であるloess()では同じようなことをつぎのようにすることができる
  - 回帰式 $y4~x$ としたうえで、Localの範囲指定がfではなくspanとなっている。こちらでは多項式の次数をdegreeで指定している(逆に言えばlowess()の方は１次多項式近似していることがわかる)。また、重みづけ関数の指定はない(weightsなる引数があるが、これは、そもそものデータ点に重みをつけるもののようであって、Local範囲の点の重みづけ関数のことではないようだ)。predict()はloess()の出力と座標から、指定した座標の推定値を計算して返す関数

loess.out <- loess(y4~x,span=0.5,degree=1)
plot(x,y4)
lines(lowess.out,col=2)
lines(cbind(t,predict(loess.out,t)),col=3)
# 重なり過ぎてわかりにくいのでy軸方向に少し平行移動した線も描く
lines(cbind(t,predict(loess.out,t)+0.1),col=4)

- lowess()がloess()に含まれる(らしい)ことがわかったので、以下、loess()の挙動を確認する
- まずは近所の範囲指定を変えてみる

plot(x,y4,col=gray(0.9))
spans <- seq(from=0.1,to=0.9,by=0.1)
for(i in 1:length(spans)){
	loess.out <- loess(y4~x,span=spans[i],degree=1)
	lines(cbind(t,predict(loess.out,t)),col=i+1)

}
legend(0,-0.3, c(paste("f = ", spans)), lty = 1, col = 1+(1:length(spans)))

- 次にデータのばらつきを変えてみる

par(mfcol=c(3,3))
sds <- seq(from=0.1,to=0.9,by=0.1)
for(i in 1:length(sds)){
	x <- t+rnorm(length(t),0,sds[i])
	plot(x,y4,cex=0.1,pch=20)
	loess.out <- loess(y4~x,span=0.5,degree=2)
	lines(cbind(t,predict(loess.out,t)),col=2)
}
par(mfcol=c(1,1))

- - 推定線を重ねてみよう

plot(t,y4,type="l")
sds <- seq(from=0.1,to=0.9,by=0.1)
for(i in 1:length(sds)){
	x <- t+rnorm(length(t),0,sds[i])
	#plot(x,y4,cex=0.1,pch=20)
	loess.out <- loess(y4~x,span=0.5,degree=2)
	lines(cbind(t,predict(loess.out,t)),col=i+1)
}

- loess()の近似式には、「どれくらい複雑」にしたか、と言う情報がある。自由度(のようなもの)のこと。loess.out$enpで出る。線を表すのに必要とするパラメタの数に相当する値
- 一方、スプラインの方は、この自由度を指定して関数を得ることもできる
  - スプライン法では、すべての点を通る折れ線をベースにして、「それじゃあ、折れ曲がりがきつすぎる」から、そこを滑らかにする、という戦略。x軸に沿って隣り合う２点に多項式を作る。作るにあたって、隣り合う多項式は、つながること(０次微分が同じ)、傾きも同じ(１次微分が同じ)を条件に、２次微分が小さくなるように選ぶ
  - こうするとたくさんのパラメタを使うことになるが、そのパラメタの数が何個分か、に相当する(らしい)
  - 自由に引かせれば

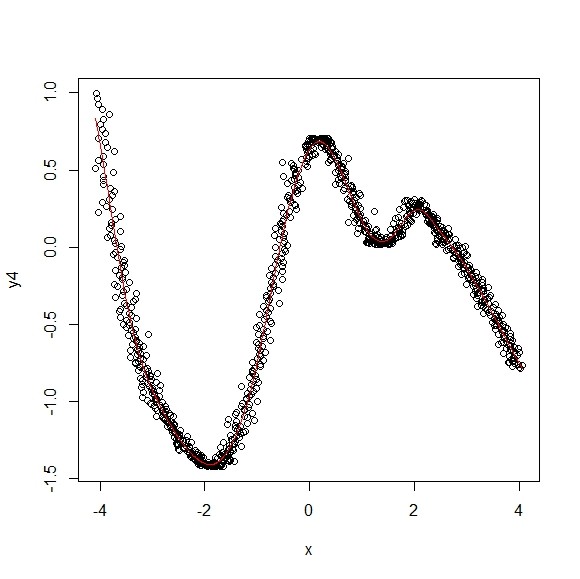
x <- t+rnorm(length(t),0,0.1)
plot(x,y4)
spline.out <- smooth.spline(x,y4)
lines(spline.out,col=2)

- - loess()の出力の自由度相当値を見て、それを指定してスプラインを引くこともできる
    - そうするとスプラインとloess()の結果が相当近くなる

x <- t+rnorm(length(t),0,0.1)
plot(x,y4)
loess.out <- loess(y4~x,span=0.5,degree=2)
# 自由度相当値
loess.out$enp
spline.out <- smooth.spline(x,y4)
spline.out.2 <- smooth.spline(x,y4,df=loess.out$enp)
plot(x,y4)
lines(spline.out,col=2)
lines(spline.out.2,col=3)
lines(cbind(t,predict(loess.out,t)),col=4)

- Additive Nonparametric Regressionのmgcvパッケージのgam()を使ってやってみる
  - この関数では、推定がレコードのxに対しては出るけれど、そうでない値に対しては出ない。その点について留意して以下のソースを確認
  - もちろんこの方法は、多変量のためにあるので、詰まらない結果になるが…

library(mgcv)
# xについてlocal処理をするにはy~s(x)。これをy~xとするとただの線形回帰になる
gam.out <- gam(y4~s(x))
gam.out.lin <- gam(y4~x)
plot(x,y4)
lines(cbind(x,predict(gam.out,data.frame(x))),col=2)
lines(cbind(x,predict(gam.out.lin,data.frame(x))),col=3)

- 多次元データにしよう
  - 視覚化して意味がわかるのは２次元なので、実行は２次元
  - スプラインは多次元化が難しいので、lowess()とgam()との比較をする
  - 面を作ってみよう

n <- 100
t <- seq(from=-3,to=3,length=n)

XY <- expand.grid(t,t)
R <- sqrt(apply(XY^2,1,sum))
z1 <- (1-R^2)*exp(-R^2/2)
z2 <- abs((R-2)/3)
z3 <- 5/(R+5)
z4 <- sin(XY[,2]/3)
z5 <- abs(z1-2*z2+z3-z4)
persp(t,t,matrix(z5,length(t),length(t)),shade=0.5,theta=70,phi=70)

library(rgl)
plot3d(cbind(XY,z5))

- - データにばらつきを入れる。表示の都合上、Z値をばらつかせることしかできないpersp表示と、XY座標をばらつかせられるplot3d()があるが、推定ではXYもバラバラしている方がよいのでそちらを使う

Z <- z5 + rnorm(length(z5),0,0.05)
persp(t,t,matrix(Z,length(t),length(t)),shade=0.5,theta=70,phi=70)

library(rgl)
XY.2 <- XY + rnorm(length(unlist(XY)),0,0.05)
plot3d(cbind(XY.2,z5))

- - loessで推定してみよう

n <- 100
t <- seq(from=-3,to=3,length=n)

XY <- expand.grid(t,t)
R <- sqrt(apply(XY^2,1,sum))
z1 <- (1-R^2)*exp(-R^2/2)
z2 <- abs((R-2)/3)
z3 <- 5/(R+5)
z4 <- sin(XY[,2]/3)
z5 <- abs(z1-2*z2+z3-z4)
persp(t,t,matrix(z5,length(t),length(t)),shade=0.5,theta=70,phi=70)

Z <- z5 + rnorm(length(z5),0,0.05)
persp(t,t,matrix(Z,length(t),length(t)),shade=0.5,theta=70,phi=70)

library(rgl)
XY.2 <- XY + rnorm(length(unlist(XY)),0,0.05)
plot3d(cbind(XY.2,z5))

my.data <- data.frame(z=z5,x=XY[,1],y=XY[,2])
loess.out <- loess(z~x+y,data=my.data,span=0.5,degree=1)
TT <- expand.grid(x=t,y=t)
predict.loess <- predict(loess.out,TT)
persp(t,t,matrix(predict.loess,length(t),length(t)),theta=70,phi=70,shade=0.5)

- - 次数を上げて、近場の範囲を減らしてみる

loess.out <- loess(z~x+y,data=my.data,span=0.1,degree=2)
TT <- expand.grid(x=t,y=t)
predict.loess <- predict(loess.out,TT)
persp(t,t,matrix(predict.loess,length(t),length(t)),theta=70,phi=70,shade=0.5)

- - Addtive nonparametricでやると、x,yの２軸に関して、の評価はされているがそれらが直交に寄与しているだけである様子が見て取れる

gam.out <- gam(z~s(x)+s(y),data=my.data)
predict.gam <- predict(gam.out,TT)
persp(t,t,matrix(predict.gam,length(t),length(t)),theta=70,phi=70,shade=0.5)

- - Additive nonparametricではある変数はlocalに別の変数はいわゆる線形回帰で推定できる
    - z~s(x)+yとすれば、yの寄与は線形