2014-01-23

診断尤度比、ROC、ロジスティック回帰

２群の値分布が正規分布に従い、その正規分布の分散が等しい場合。２群は黒群が少なめ
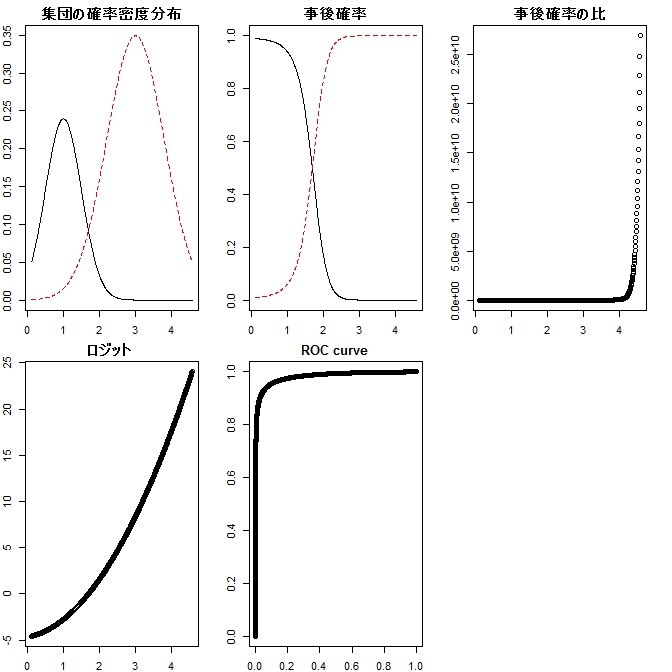
- 左上の図は、２群の確率密度分布。カーブ下面積は、群の比率になる
- 中上の図は、値ごとに２群の比率考慮の確率密度から、赤・黒それぞれの相対確率(相対尤度)を計算してプロット
- 右上の図は、その比
- 左下の図は、さらにその対数
- 中下の図は、２群の確率密度分布に基づく感度特異度が作るROCカーブ
- ロジットが直線になっていることから、 $\log{\frac{p}{1-p}}=b_0 + b_1 x$ という直線に乗っていることがわかり、これはロジスティック回帰直線。したがって、２群があって、分散が等しい正規分布になっているときに、ロジスティック回帰直線を引くことは、理にかなっている。

# ms は２群の値の平均
# sdsは２群の値の標準偏差
# rは２群のうちの第１群の割合
# thresはプロットするときの範囲を制限するための変数
my.ROC.logit.norm <- function(ms,sds,r,thres=0.05){
	# xは計算する値のベクトル
	x <- seq(from = min(ms)-max(sds)*3,to=max(ms)+max(sds)*3,length=1000)
	# 平均・標準偏差を入れ直して
	m1 <- ms[1];m2 <- ms[2]
	s1 <- sds[1];s2 <- sds[2]
	# 群の占める割合を加味した確率密度分布(正規分布を仮定している)
	d1 <- dnorm(x,m1,s1)*r
	d2 <- dnorm(x,m2,s2)*(1-r)
	# 値ごとの２群のそれぞれの相対確率
	q1 <- d1/(d1+d2)
	q2 <- d2/(d1+d2)
	# 群ごとの累積分布
	p1 <- pnorm(x,m1,s1)
	p2 <- pnorm(x,m2,s2)
	# snは感度、spは特異度。感度特異度は、群ごとの累積分布で決まる
	sn <- 1-p1
	sp <- p2
	# 値ごとの、群2である確率Qに関するQ/(1-Q)
	lg <- q2/q1
	# プロット範囲を定める(２群の割合がまあまあある範囲に限定)
	X <- which(d1+d2>thres)
	
	my.par <- par(mfrow=c(2,3),mar=rep(2,4));on.exit(my.par)
	matplot(x[X],cbind(d1,d2)[X,],type="l",main="集団の確率密度分布")
	matplot(x[X],cbind(q1,q2)[X,],type="l",main="事後確率")
	plot(x[X],lg[X],main="事後確率の比")
	plot(x[X],log(lg[X]),main="ロジット")
	plot(sn,1-sp,main="ROC curve")
}

m1 <- 1
m2 <- 3
s1 <- 0.5
s2 <- 0.5

r <- 0.3

my.ROC.logit.norm(c(m1,m2),c(s1,s2),r)

２群の分散を変えてみる

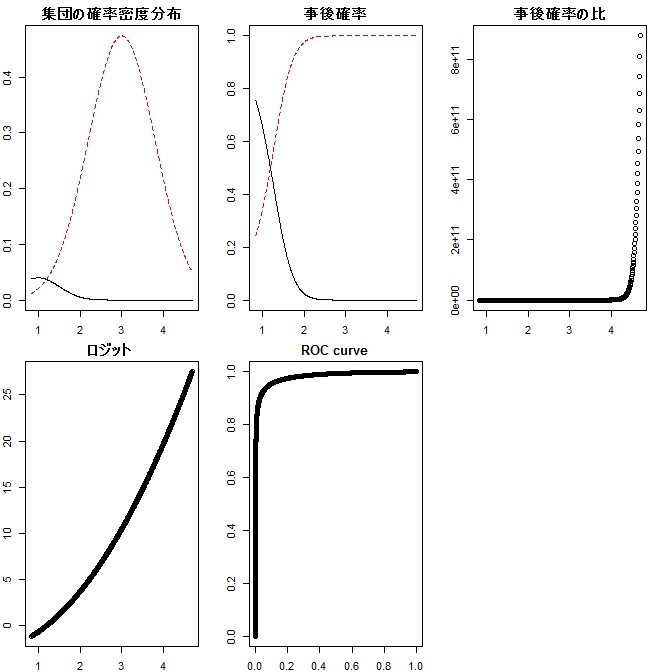
- 左下のロジットが直線ではなくなった→、ロジスティック直線回帰にはずれがあることがわかる

m1 <- 1
m2 <- 3
s1 <- 0.5
s2 <- 0.8 # 変えた！
r <- 0.3
my.ROC.logit.norm(c(m1,m2),c(s1,s2),r)

ROCカーブとロジット・事後確率比との関係
- カットオフの値を増やして行くと、ROCカーブは右上から、左下に向かって進む。
- 事後確率比は、ROCカーブの傾き。ROCカーブの右上のとき(カットオフが小さい値のとき)には、ROCカーブの傾きは0であり、確かに、右上の図の左端で事後確率の比が0付近にある。ROCカーブが左下のとき(カットオフが大きい値のとき)には、ROCカーブの傾きは無限大であり、確かに、右上の図の右端で事後確率の比が無限大に発散している
診断尤度比は、この「事後確率の比」のこと
- ２群の相対比を変化させてプロットしてみる

- 何が変わったのかわかりづらいかもしれないが、左上の図は、黒・赤の高さが変わっており、これが２群の比率の変化に相当する。中上の図も交叉点が左にずれることで変わっている。これは、赤と判断するべき値がより左の値のときにずれていることを表している。右上の図は形は同じだが、縦軸のスケールが違うことに注意する。左下の図も形は同じだが、縦軸のスケールが大きくなっている(赤と判断するべき、とシフトしている)。中下のROCカーブは２群の比によらず、群ごとの分布によるカーブなので、変化していない。

m1 <- 1
m2 <- 3
s1 <- 0.5
s2 <- 0.8

r <- 0.05 # 変えた!

my.ROC.logit.norm(c(m1,m2),c(s1,s2),r)

少し変なことをしてみよう
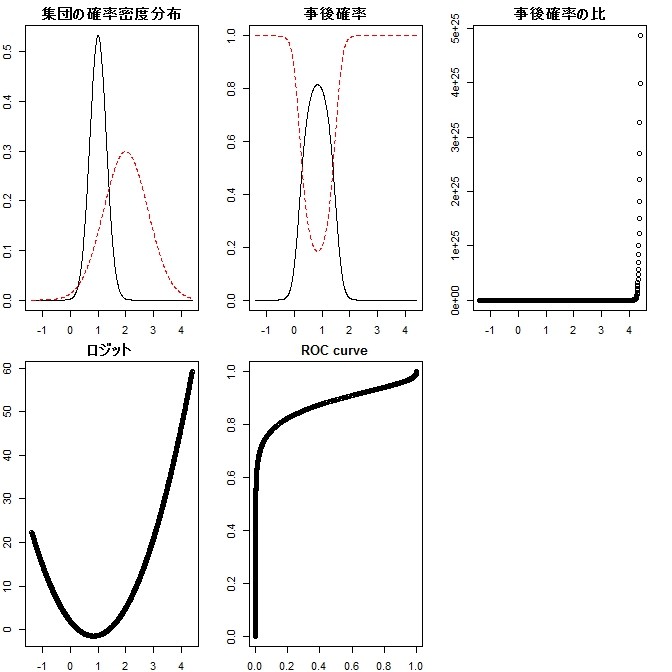
- ２群の比はまあまあ均等、２群の平均はまあまあ離れているが、２群の分散にかなり違いがあるとする
- こうすると、中上の事後確率では、値が小さいときと大きいときの両方で赤らしさが高まる。値が大きいときの赤らしさは「本物」で、値が小さいときの赤らしさは、嘘ではないけれど、母数が少ないときに相当する。
- これに対応して、ロジットも単調増加ではなくなっている
- ROCカーブの傾きは、事後確率の比であるのだが、それを反映して、中下のROCカーブの右上端に向かって(カットオフを小さくしていくに従って)、傾きが単調に減少するのではなく、減少から増加に転じていることがわかる。
- 逆に言えば、ROCカーブが単調増で凸であるということは、事後確率の比が単調増であることで、ROCカーブに変曲点が入るのは、事後確率の比・ロジットが単調でないことに対応していることがわかる。

m1 <- 1
m2 <- 2
s1 <- 0.3
s2 <- 0.8

r <- 0.4

my.ROC.logit.norm(c(m1,m2),c(s1,s2),r,thres=0)