二次形式なLoss fucntion - ryamadaの遺伝学・遺伝統計学メモ

こちらでGaussian Sequence Modelをなぞっている
遅々として進まないのだが、まあそれはよいとして、今は、Loss functionとして二次形式なもので正定値な行列を挟んだものを使うと、Bayesian estimatorは観測値に基づく真値の事後分布の期待値になるよ、それはどんな正定値行列を用いた二次形式なLoss functionでもそうだよ、というベイジアンな式変形のところで時間がかかっている
まず、正定値行列を使った二次形式云々についてはこちらで確認
正定値二次形式になっているときに、それを最小化する推定値を求めるのは、こちらの「行列の微分と導関数」というスライドを眺めると「はは〜」とわかる
なので、読んでいるPDFで $E(\theta|y)$ を推定値にすると最小化するよ、というところまでは追える。それが正定値行列を含んでいないから、Loss functionの取り方によらない(正定値行列を使った二次形式でありさえすれば)ということもわかる
でも、やっぱり、納得行かないので、Rでやってみる

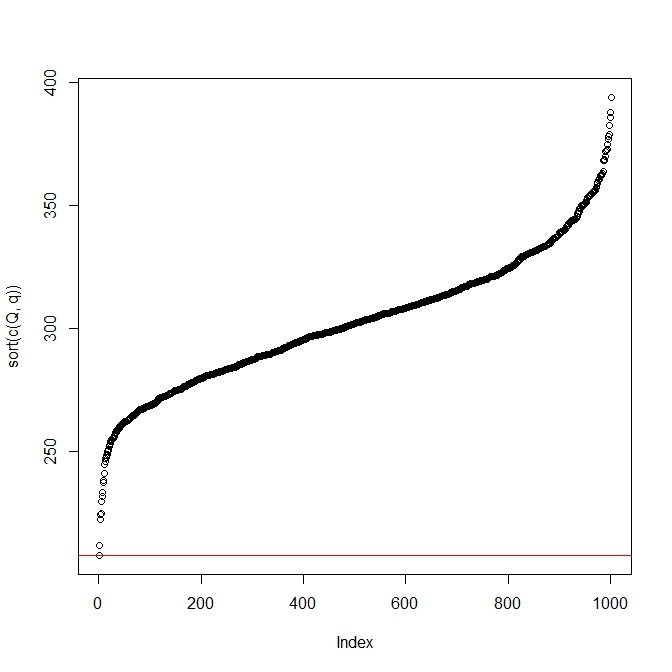
期待値がわかっているとしたら、それを用いたLoss functionの値(赤い水平線)が、ランダムに調べた推定値の場合のLoss function値と比べて最小であることがわかる

# 観測対象数
n <- 100
# その真値は適当(正規分布などとは似ても似つかない)
theta <- rexp(n)
# 真値があったときに、どのような観測値が得られるか、というのは
# たいていの場合、真値を中心にした正規分布を取るわけだけれど
# この議論はそんな「普通の場合」だけでなく、「どんな場合でも、いつでも」成り立つ
# ということを言っているので、次のようにする
# yの値によらず適当にしかも平均しても0にならないような
# ずれが生じるという背景があり、それをzとする
z <- rnorm(1,0.2,2)
# その上で、そのsystematic なずれに加えて乱雑項も入れておく
# ただし、この乱雑項は0を中心とした正規分布としておく
# そうしておけば、yを見たときの真値の期待値はy-zと「わかって」いるから
# 実際のデータを扱うときには、これが「わかって」いないので苦労するけれど
# 今は、「わかって」いたとしたら…という話

# これが観察値
y <- theta + z + rnorm(n,0,2)

# さて、適当に正定値行列を作って、それに基づく二次形式Loss functionを定めよう

library(GPArotation)

n <- n
d <- rnorm(n)
d <- runif(n)
R <- Random.Start(n)
M <- R %*% diag(d) %*% t(R)

# 観察値付近をランダムに探索して、それを「推定値」としたときの
# 真値からのLoss functionの値を計算して格納する
n.iter <- 1000
q <- rep(0,n.iter)
L <- q
for(i in 1:n.iter){
	tmp <- y + rnorm(n)
	q[i] <- t(tmp-theta) %*% M %*% (tmp-theta)
	L[i] <- sum((tmp-theta)^2)
}
# 「期待値y-z」が「わかって」いるとすれば、そのときのLoss fucntionの値も計算できる
Q <- t(y-z-theta) %*% M %*% (y-z-theta)

plot(sort(c(Q,q)))
abline(h=Q,col=2)