2014-07-02

医学を作るシミュレーション

R 医学

医学を単純化するとどうなるかやってみる(こちらの『知識ゼロからの診療』のための模擬設定)
生物が必要
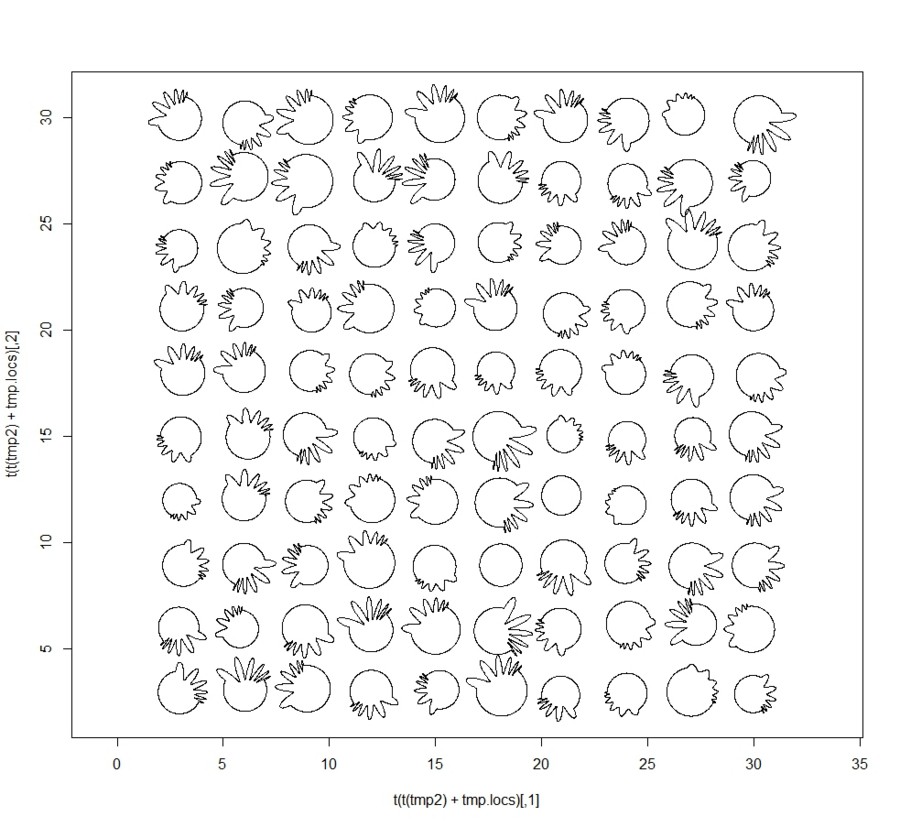
生物に多様性を持たせることが必要
病気が必要
病気の定義が必要
- 構造障害・機能障害(解剖・生理)
因果推論が必要
治療が必要
まずは生物の構造を設定

解剖学を学ぼう！
- 「丸っこい部分」と「突起が並んだ部分」に分かれます
  - 名前をつけよう。『丸領域』『突起域』
    - どうして名前をつける？
  - 突起は５本ある。時計回りに手前からだんだん小さくなる。順番をつけて呼ぶことにしよう。『第１突起』『第２突起』…『第５突起』
  - ２つの突起の谷間にも名前をつけよう。『第１谷』『第２谷』…『第４谷』
生理学を学ぼう！
- この生物は反時計回りに回ります
- 回る速さは個体によって違いますが、速すぎず、遅すぎずです
- どんな風に観測しましょうか
- 速さを表現する方法が必要なので、単位時間あたり何度回るかで表すことにしましょう
症候学を学ぼう！
- 症状
  - 「おなかが張るんです」
  - 「くらくらするんです」
- 徴候
  - たしかにおなか(丸領域)が出っ張っている：「丸領域突出」
  - 動きが滑らかではない：「非平滑回転」
病気の原因を突き止めよう、病理学を学ぼう！
- 「丸領域突出」の原因は、内部にたまった物質だった
  - それには２種類あった
- 「非平滑回転」の原因は、体内に入った、虫だった
- 本当にそれは「原因」だったのか？
  - どうやって、「本当の原因」と確信する？
病名をつける
- 「丸領域突出病」
- 「回転がたがた病」
- どうして病名をつける？
治療法を編み出そう！
- 「原因を取り除こう」
- 「調子を整えよう」
- 本当に効いているのかを確かめる

t <- seq(from=0,to=1,length=1000)*2*pi
r <- rep(1,length(t))
x <- cos(t)
y <- sin(t)

n.ind <- 25
par(mfcol=c(5,5))
for(i in 1:n.ind){
k<-11
k2 <- 3
k3 <- 0.2 + rnorm(1)*0.08
k4 <- 2.5 + rnorm(1)*0.05
k5 <- rnorm(1,1,0.1)
R <- sin(k*t) * (1+sin(t/k2))

rR <- r
rR[1:(length(t)/2)] <- rR[1:(length(t)/2)] + R[1:(length(t)/2)] * k3

X <- rR * x
Y <- rR * y

XY <- cbind(X,Y)
theta <- pi/3
R <- matrix(c(cos(theta),sin(theta),-sin(theta),cos(theta)),2,2)

XY. <- R %*% t(XY)
X <- XY.[1,]
Y <- XY.[2,]
#plot(X,Y,type="l")

K <- X + 1i * Y
K.mod <- Mod(K)
K.arg <- Arg(K)
K.arg[which(K.arg < 0)] <- K.arg[which(K.arg < 0)] + 2*pi

#plot(K.arg)

K.arg.2 <- (K.arg/(2*pi))^k4 * 2*pi

X.2 <- K.mod * cos(K.arg.2)
Y.2 <- K.mod * sin(K.arg.2)
X.2 <- X.2 * k5
Y.2 <- Y.2 * k5
plot(X.2,Y.2,type="l",frame.plot=FALSE,axes=FALSE,asp=TRUE,xlab="",ylab="")

}
par(mfcol=c(1,1))


n.ind <- 100

aerians <- list()
for(i in 1:n.ind){
k<-11
k2 <- 3
k3 <- 0.2 + rnorm(1)*0.08
k4 <- 2.5 + rnorm(1)*0.05
k5 <- rnorm(1,1,0.1)

R <- sin(k*t) * (1+sin(t/k2))

rR <- r
rR[1:(length(t)/2)] <- rR[1:(length(t)/2)] + R[1:(length(t)/2)] * k3

X <- rR * x
Y <- rR * y

XY <- cbind(X,Y)
theta <- pi/3
R <- matrix(c(cos(theta),sin(theta),-sin(theta),cos(theta)),2,2)

XY. <- R %*% t(XY)
X <- XY.[1,]
Y <- XY.[2,]
#plot(X,Y,type="l")

K <- X + 1i * Y
K.mod <- Mod(K)
K.arg <- Arg(K)
K.arg[which(K.arg < 0)] <- K.arg[which(K.arg < 0)] + 2*pi

#plot(K.arg)

K.arg.2 <- (K.arg/(2*pi))^k4 * 2*pi

X.2 <- K.mod * cos(K.arg.2)
Y.2 <- K.mod * sin(K.arg.2)
X.2 <- X.2 * k5
Y.2 <- Y.2 * k5

aerians[[i]] <- cbind(X.2,Y.2)

}

locs <- as.matrix(expand.grid(1:10,1:10))*3
my.rot <- function(p,X){
	R <- matrix(c(cos(p),sin(p),-sin(p),cos(p)),2,2)
	t(R %*% t(X))
}

p <- runif(n.ind)*2*pi
q <- runif(n.ind)*0.1

too.quick <- sample(1:n.ind,1)
#q[too.quick] <- pi

random.locs <- matrix(rnorm(n.ind*2),ncol=2)*0.1
n.time <- 100
Z <- list()
for(j in 1:n.time){
	tmp.full <- matrix(0,0,2)

for(i in 1:n.ind){
	if(i==1){
		tmp <- aerians[[i]]
		tmp2 <- my.rot(p[i]+j*q[i],tmp)
		tmp.locs <- locs[i,]
		tmp.locs <- tmp.locs + random.locs[i,]
		if(j==1){
		xlim=c(min(locs)-1,max(locs)+1)
		ylim=c(min(locs)-1,max(locs)+1)
		}
		#plot(t(t(tmp2)+tmp.locs),type="l",xlim=xlim,ylim=ylim,asp=TRUE)
		tmp.full <- rbind(tmp.full,t(t(tmp2)+tmp.locs))
	}else{
		tmp <- aerians[[i]]
		tmp2 <- my.rot(p[i]+j*q[i],tmp)
		tmp.locs <- locs[i,]
		tmp.locs <- tmp.locs + random.locs[i,]

		#points(t(t(tmp2)+tmp.locs),type="l")
		tmp.full <- rbind(tmp.full,t(t(tmp2)+tmp.locs))

	}
	
}
Z[[j]] <- tmp.full
#plot(tmp.full,xlim=xlim,ylim=ylim,pch=20,cex=0.2,frame.plot=FALSE,axes=FALSE,asp=TRUE,xlab="",ylab="")
#Sys.sleep(0.001)
}

for(i in 1:n.time){
	plot(Z[[i]],xlim=xlim,ylim=ylim,pch=20,cex=0.2,frame.plot=FALSE,axes=FALSE,asp=TRUE,xlab="",ylab="")
}


k<-11
k2 <- 3
k3 <- 0.2 
k4 <- 2.5 
k5 <- 1
R <- sin(k*t) * (1+sin(t/k2))

rR <- r
rR[1:(length(t)/2)] <- rR[1:(length(t)/2)] + R[1:(length(t)/2)] * k3

# 丸部突出病
k6 <- 0.2
R2 <- rep(1,length(t))
R2[which(abs(x)<k6)] <- R2[which(abs(x)<k6)] * (1+2*(k6-abs(x[which(abs(x)<k6)])))
rR[(length(t)/2+1):length(t)] <- rR[(length(t)/2+1):length(t)] * R2[(length(t)/2+1):length(t)]


X <- rR * x
Y <- rR * y

XY <- cbind(X,Y)
theta <- pi/3
R <- matrix(c(cos(theta),sin(theta),-sin(theta),cos(theta)),2,2)

XY. <- R %*% t(XY)
X <- XY.[1,]
Y <- XY.[2,]
plot(X,Y,type="l")

K <- X + 1i * Y
K.mod <- Mod(K)
K.arg <- Arg(K)
K.arg[which(K.arg < 0)] <- K.arg[which(K.arg < 0)] + 2*pi

#plot(K.arg)

K.arg.2 <- (K.arg/(2*pi))^k4 * 2*pi

X.2 <- K.mod * cos(K.arg.2)
Y.2 <- K.mod * sin(K.arg.2)
X.2 <- X.2 * k5
Y.2 <- Y.2 * k5
plot(X.2,Y.2,type="l",frame.plot=FALSE,axes=FALSE,asp=TRUE,xlab="",ylab="")

ss <- which(abs(x)<k6 & t > t[length(t)/2])
minss <- min(ss)
maxss <- max(ss)
centerss <- mean(c(minss,maxss))

my.centralize <- function(X,r){
	ctr <- apply(X,2,mean)
	t((t(X)-ctr) * r +ctr)
}



ctr <- apply(xxyy,2,mean)

xx <- X.2[c(minss,centerss,maxss)]
yy <- Y.2[c(minss,centerss,maxss)]
xxyy <- cbind(xx,yy)
xxyy.2 <- my.centralize(xxyy,0.9)

polygon(xxyy.2[,1],xxyy.2[,2],col="red")

くらくら病：赤

col <- rep(1,length(Z[[1]][,1]))
col[((too.quick-1)*length(t)+1):(too.quick*length(t))] <- 2
for(i in 1:n.time){
	if(i == too.quick)col=3
	plot(Z[[i]],xlim=xlim,ylim=ylim,pch=20,cex=0.2,frame.plot=FALSE,axes=FALSE,asp=TRUE,xlab="",ylab="",col=col)
}
library(animation)
saveGIF({

for(i in 1:n.time){
	plot(Z[[i]],xlim=xlim,ylim=ylim,pch=20,cex=0.2,frame.plot=FALSE,axes=FALSE,asp=TRUE,xlab="",ylab="",col=col)
}
},interval=0.05)

gif->swf "GIF2SWF Converter" フリーアプリで