2014-04-22

Non-negative Matrix Factorization

こちらの論文で腫瘍のシークエンスデータを用いて、変異の入った遺伝子とそうでない遺伝子との情報を行列化し、それにNon-negative Matrix Factorizationを使って腫瘍のクラスタリング、特性(治療反応性とか)予測、特性に影響しているパスウェイ検出などを行っている
そのNon-negative Matrix Factorizationについて
まず、非負の行列を使う。遺伝子発現データとか、分子反応系ネットワークとかは、この世にあるもの(正のもの)同士の相互作用なので、「非負」で扱いたい、というような背景があるらしい。今回の変異があるかどうかについてもその延長線上として非負行列を使う
$A\times B$ 行列があったとき、それを $A\times C$ 行列と $C\times B$ 行列の積に分解する
元の行列には $A\times B$ の要素があり、分解した後の行列には $A\times C+B\times C=(A+B)\times C$ の要素がある。 $C$ が大きな数でないと、断然 $(A+B)\times C$ という要素数は少ない。したがって、分解する前の行列を、分解すると、少ない要素数で説明しなくてはならなくなる。うまく分解できたとしても『近似』になっている。どういう風に分解して、元の情報を劣化させない基準をどうするか、という「気持ち」が背景に動いた上で分解されるが、いずれにしろ「近似結果」が得られる
また、 $A$ がサンプル数、 $B$ が観測マーカー数であるとすると、分解後には $A\times C$ の行列が片方に得られていて、これは、 $A$ 個のサンプルを $C$ 次元空間の点に対応づけていることになっている。その $C$ 次元空間の点への対応づけは、「分解〜近似」を支える、もう片方の $C\times B$ 行列の方に、「こういう視点で眺めれば」という情報が入っている
以上のような方法である
やってみよう
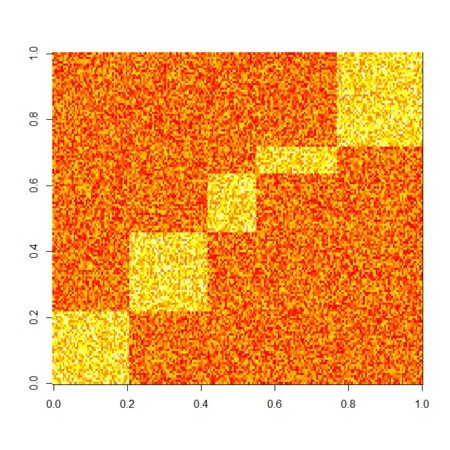
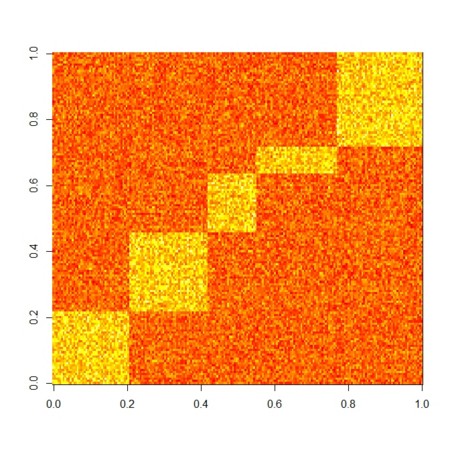
まず、n群に分かれるデータを適当に作って、乱雑項を入れる

n <- 5
v1 <- sample(10:50,n)
v2 <- sample(10:50,n)
col <- c()
for(i in 1:n){
	col <- c(col,rep(i,v1[i]))
}
M <- sum(v1)
N <- sum(v2)
X <- matrix(0,M,N)
m1 <- m2 <- 1
for(i in 1:n){
	X[m1:(m1+v1[i]-1),m2:(m2+v2[i]-1)] <- 0.5
	m1 <- m1+v1[i]
	m2 <- m2+v2[i]
}
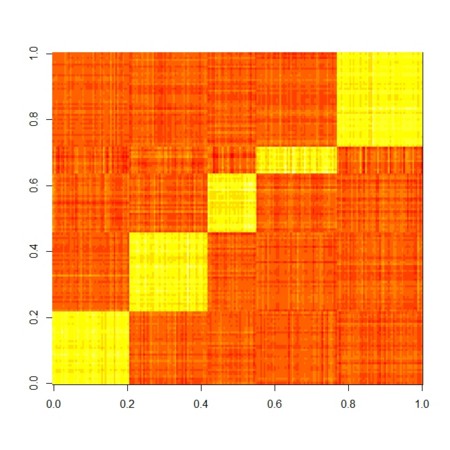
X. <- X + runif(length(X))
image(X.)

次に、これをRのNMFNパッケージのnnmf()関数でNon-negative matrix factorizationする。手法選択引数があるが、ここはデフォルトで回すこととし、 $(A\times C),(C\times B)$ の $C$ の値を1,2,3,4,5,6,10,100と変化させてみる
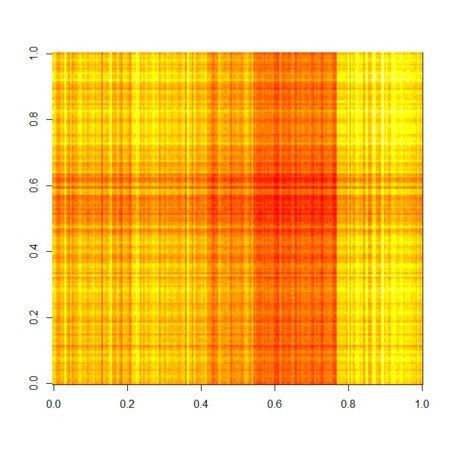
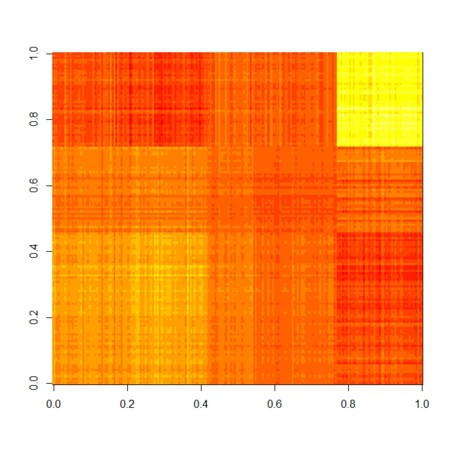
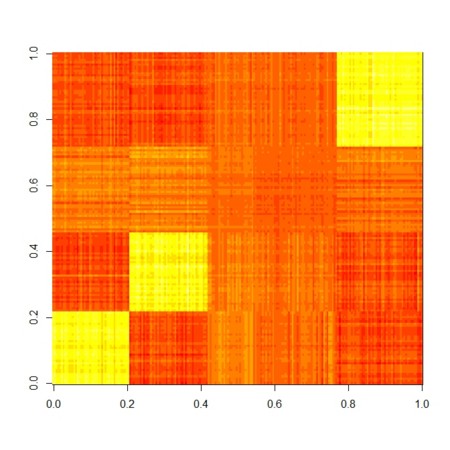
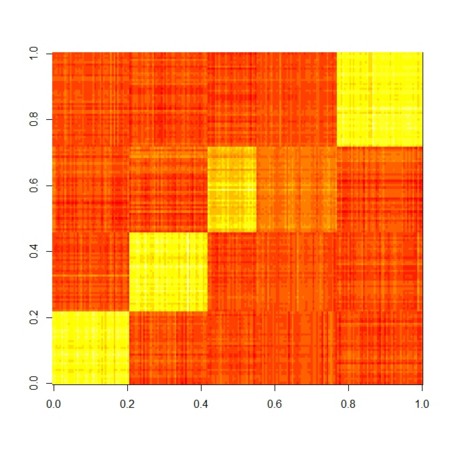
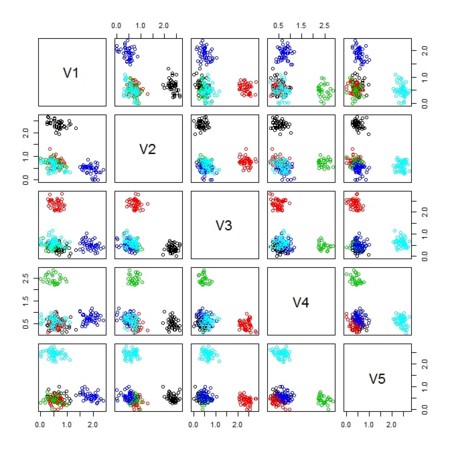
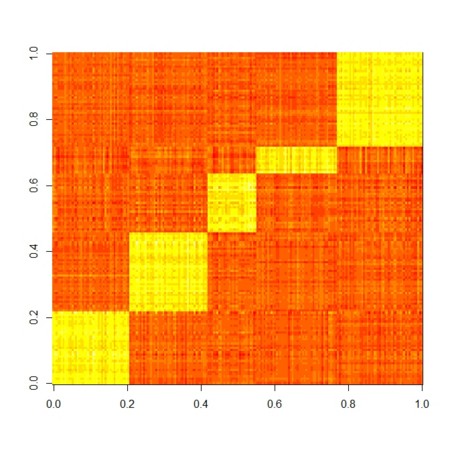
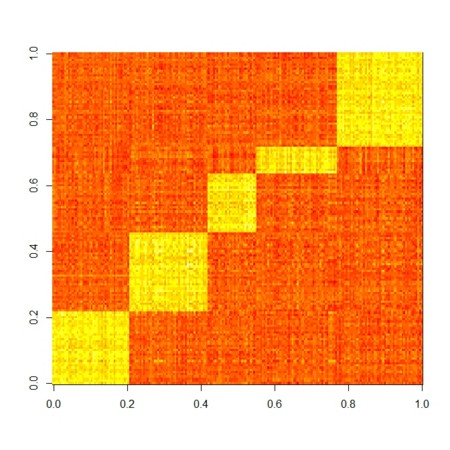
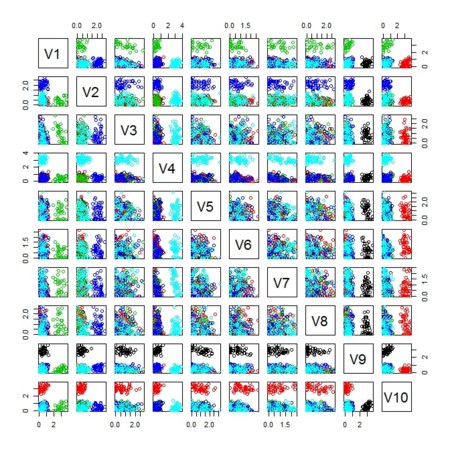
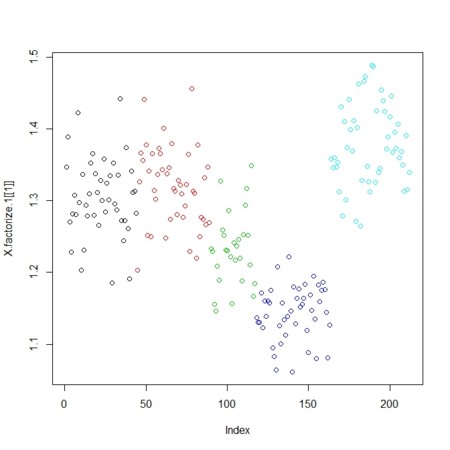
nnmf()後には、分解〜近似結果が得られるので、どのくらいに近似されたかを図示とともに、という行列に現れる「クラスタリングの様子」を同じく図示す
- X.factorize.k1に $A\times C$ 行列が、X.factorize.k2に $C\times B$ 行列が返っている
- $C=1$

- $C=2$

- $C=3$

- $C=4$

- $C=5$

- $C=6$

- $C=10$

- $C=100$

library(rgl)
library(NMFN)
X.factorize.1 <- nnmf(X.,1)
image(X.factorize.1[[1]]%*%X.factorize.1[[2]])
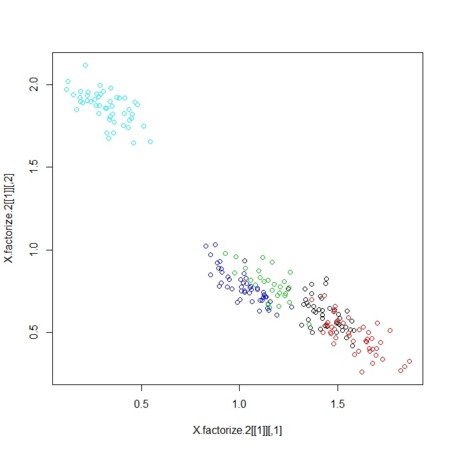
plot(X.factorize.1[[1]],col=col)

X.factorize.2 <- nnmf(X.,2)
image(X.factorize.2[[1]]%*%X.factorize.2[[2]])
plot(X.factorize.2[[1]],col=col)

X.factorize.3 <- nnmf(X.,3)
image(X.factorize.3[[1]]%*%X.factorize.3[[2]])
plot3d(X.factorize.3[[1]],col=col)
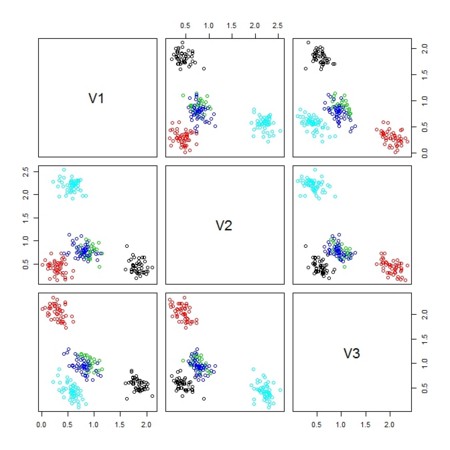
plot(as.data.frame(X.factorize.3[[1]]),col=col)

X.factorize.4 <- nnmf(X.,4)
image(X.factorize.4[[1]]%*%X.factorize.4[[2]])
plot(as.data.frame(X.factorize.4[[1]]),col=col)

X.factorize.5 <- nnmf(X.,5)
image(X.factorize.5[[1]]%*%X.factorize.5[[2]])
plot(as.data.frame(X.factorize.5[[1]]),col=col)

X.factorize.6 <- nnmf(X.,6)
image(X.factorize.6[[1]]%*%X.factorize.6[[2]])
plot(as.data.frame(X.factorize.6[[1]]),col=col)

X.factorize.10 <- nnmf(X.,10)
image(X.factorize.10[[1]]%*%X.factorize.10[[2]])
plot(as.data.frame(X.factorize.10[[1]]),col=col)

X.factorize.100 <- nnmf(X.,100)
image(X.factorize.100[[1]]%*%X.factorize.100[[2]])