2014-06-22

Dirichlet diffusion trees

先日の記事の続き
昨日の木はDirichlet diffusion treeの分岐プロセスをグラフオブジェクトに乗せて作る話だった
昨日の記事では、分岐確率を時刻の関数とし、さらに、各エッジで同道している「先行者」の数で重みづけすることを述べたが実装は面倒なので省略した
今日は、その面倒を実装
まず、時刻tの関数として、分岐確率関数が $a(t)$ で与えられているとする
いつ分岐するか、というと、 $A(t)=\int_0^t a(u) du$ で「時刻tに分岐する」とは「分岐関数 $a(t)$ に照らして、時刻tの直前までは分岐しない」ということなので、積分が効いていることを表している
今、そんな $A(t)$ に関して、いつごろ分岐する？というのを乱数で発生しようとすると $A^{-1}(u)$ なる関数( $A(t)$ の逆関数)を考えて、乱数発生のところは $e ~ Exp$ のように指数乱数を与えるとよい
「同道者」の数がmいるなら、 $A^{-1}(m\times e)$ のようにして得られる
また、セグメントで考えるときには、ある時刻 $t_k$ から $t_{k+1}$ の間に分岐が起きてほしいのだが、時刻 $t_k$ までに起きる分は関係なく、 $a(t_k)$ から分岐確率を積分しその逆関数を考えたくなるのだが、それは $A^{-1}(A(t_k) + m \times e)$ で乱数発生させればよい
また、この $A(t_k)$ というのは、時刻0なら $A(0)=\int_0^0 a(u) du=0$ だし、それ以外の時刻であれば、分岐を生成するときに $A(t_{k'})+m \times e$ を指数乱数 $e$ を使って生成し、そこから $A^{-1}()$ を計算したわけであるから、この $A(t_{k'})+m \times e$ がこの $A(t_k)$ に相当している
したがって、モデルを考えるときに、 $a(t)$ が大事だが、計算上、用いるのは $A^{-1}(e)$ だけ
ちなみに、 $a(t) = \frac{c}{1-t}$ というような関数の場合 $A^{-1}(e) = 1-exp(-e/c)$ である(単純に、積分して逆をとる)。この $a(t)$ は時刻とともにどんどん確率が大きくなって、時刻1で無限大に発散するような関数。このような関数は、「無限大」に発散しているから、 $A(t)$ も無限大に発散するし、「必ずいつか分岐する」という関数
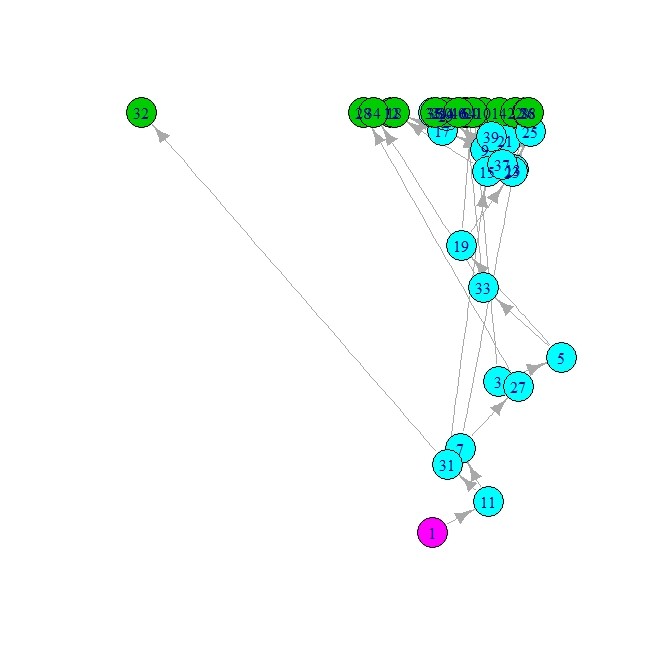
以下の例では、c=1でこれを試している

library(igraph)
# a(t) = c/(1-t)なる分岐確率関数のA^{-1}(e)関数。xに指数乱数(を修飾した値)を与える
fx <- function(x){
	k <- 1
	1-exp(-x/k)
}
# 20個の軌跡を作る
n.pt <- 20
# 最初の1個。原点を表すノードID１と最初の葉ノードになるIDの２をエッジリストで与える
el <- matrix(c(1,2),nrow=1)
Leaves <- c(2)
Root <- c(1)
g <- graph.edgelist(el)
# この１本のエッジの長さは1
E(g)$weight <- c(1)
plot(g)
g.hx <- list()
g.hx[[1]] <- g
# ノードの「時刻」情報(原点は０、葉ノードは１、分岐点は(0,1)の値
t <- c(0,1)
# 分岐に関してA(t)を記録(分岐プロセスでA^{-1}(A(t)+m e)を計算するため
At <- c(0,Inf)
# 2個目以降の繰り返し
for(i in 2:n.pt){
# 親を選ぶ
	tmp.leave <- Leaves[sample(1:length(Leaves),1)]
# ルートから親である葉ノードへのパス
	tmp.path <- get.shortest.paths(g, Root, to=tmp.leave, mode = c("out"), weights = NULL, output=c("epath"))
	el.now <- get.edgelist(g)
	vnum <- vcount(g)
	e.weight <- E(g)$weight
# パスのエッジを一つずつ処理。それぞれ、分岐するならここ、という時刻をランダム発生し、
# それが「エッジの存在時間内」なら採用する。原点に近い方から最初に条件を満足したら、それが分岐点	
	tmp.d.t <- rep(0,length(tmp.path$epath[[1]]))
	path.edge.len <- e.weight[tmp.path$epath[[1]]]
	cumsum.path.edge.len <- cumsum(path.edge.len)
	for(j in 1:length(tmp.d.t)){
# 処理エッジ
		tmp.edge <- tmp.path$epath[[1]][j]
# 処理エッジの始点終点ノードＩＤ
		tmp.edge.stend <- el.now[tmp.edge,]
# 同道者数は、終点ノードから到達可能な葉ノード数
		tmp.path2 <- get.shortest.paths(g,tmp.edge.stend[2],to=Leaves)
		n.reachable.leaves <- length(which(lapply(tmp.path2$vpath,length)>0))
# 終点ノードが葉ノードであるエッジの場合、以下をして数合わせ
		if(tmp.edge.stend[2] %in% Leaves){
			n.reachable.leaves <- n.reachable.leaves+1
		}
		tmp.At <- At[tmp.edge.stend[1]]+n.reachable.leaves*rexp(1)
		tmp.d.t[j] <- fx(tmp.At)
# 分岐時刻がエッジの存在時間内かどうかの判定
		if(tmp.d.t[j] >= t[tmp.edge.stend[1]] & tmp.d.t[j] <= t[tmp.edge.stend[2]]){
			t <- c(t,tmp.d.t[j],1)
			At <- c(At,tmp.At,Inf)
			edge.len.3 <- c(tmp.d.t[j]-t[tmp.edge.stend[1]],t[tmp.edge.stend[2]]-tmp.d.t[j],1-tmp.d.t[j])
			break
		}
		
	}
# 昨日と同じ。分岐エッジが決まり、その時刻も決まったので、それに合わせて、分断されるエッジを除き、分断してできた2エッジと、分岐点から新しい葉ノードまでのエッジとを加える	
	#tmp.edge <- tmp.path$epath[[1]][sample(1:length(tmp.path$epath[[1]]),1)]
	#tmp.edge.stend <- el.now[tmp.edge,]
	el.next <- el.now[-tmp.edge,]
	el.next <- rbind(el.next,matrix(c(tmp.edge.stend[1],vnum+1,vnum+1,tmp.edge.stend[2],vnum+1,vnum+2),byrow=TRUE,ncol=2))
	Leaves <- c(Leaves,vnum+2)
	g <- graph.edgelist(el.next)
	weight.now <- e.weight[tmp.edge]
	e.weight.next <- e.weight[-tmp.edge]
	#r <- runif(1)
	#e.weight.next <- c(e.weight.next, weight.now * c(r,1-r),1)
	e.weight.next <- c(e.weight.next,edge.len.3)
	print(e.weight.next)
	E(g)$weight <- e.weight.next
	tmp.path <- get.shortest.paths(g, Root, to=vnum+2, mode = c("out"), weights = NULL, output=c("epath"))
	tmp.path.weight <- e.weight.next[tmp.path$epath[[1]]]
	last.weight <- 1-sum(tmp.path.weight[-length(tmp.path.weight)])
	e.weight.next[length(e.weight.next)] <- last.weight
	E(g)$weight <- e.weight.next
	g.hx[[i]] <- g
	
	col <- rep(5,vnum+2)
	col[Leaves] <- 3
	col[1] <- 6
	dist.from.Root <- shortest.paths(g,1)
# エッジの長さに応じて酔歩して動く距離を計算	
	tmp.dist <- rep(0,length(e.weight.next))
	for(j in 1:length(tmp.dist)){
		tmp.dist[j] <- rnorm(1,0,sqrt(e.weight.next[j]))
	}
# ノードの空間移動距離をグラフで計算するために、すべての値を正にしておく(あとで補正する)
	tmp.g <- graph.edgelist(el.next)
	E(tmp.g)$weight <- tmp.dist-min(tmp.dist)
	dist.random <- shortest.paths(tmp.g,1)
	#mean.dist.random <- mean(dist.random)
	#dist.random <- dist.random -mean.dist.random
# 空間移動をすべて正にしたが、それはすべてのエッジについて定数の下駄をはかせるやり方だったので
# 原点からの到達するのにたどったエッジの数に応じて、下駄を脱がせる
	num.seg <- unlist(lapply(get.shortest.paths(g,Root,weight=NULL)$vpath,length))
	num.seg <- num.seg-1
	num.seg[1] <- 0
	dist.random <- dist.random + min(tmp.dist)*num.seg
	coords <- matrix(c(dist.random,dist.from.Root),ncol=2)
	plot(g.hx[[i]],layout=coords,vertex.color = col)
}
par(mfcol=c(1,1))