私の今後は？潜伏期・再発

• 曝露からの時間の関数で発病率が決まるとする
• 最終的に発病しないこともあるとする
• 曝露からある時刻まで発病していないときに、その後、発病するであろう確率を知りたいことがある
  • いわゆる感染症で曝露がわかっているとき
  • 癌の術後再発
  • 遺伝性疾患で浸透率が１でないとき
• 曝露後、２回、発病しやすくなる時期があるが、それを越えると「大丈夫」だとする
  • ２つのガンマ分布の和としてシミュレーションしてみる
• ハザード関数についてはこちらも。

# 曝露からの時間
t <- 0:100
# ガンマ分布であると仮定する
# 一つ目のガンマ分布のパラメタ
a <- 50
b <- 1
# 一つ目の分布に従って発病する割合
k <- 0.4
# 二つ目のそれ
a2 <- 70
b2 <- 3
k2 <- 0.2 # トータルではk+k2の割合の人が最終的に発病する

# 確率分布と累積分布を計算
p.gamma <- k * pgamma(t,a,b) + k2 * pgamma(t,a2,b2)
d.gamma <- k * dgamma(t,a,b) + k2 * dgamma(t,a2,b2)
par(mfcol=c(1,2))
plot(t,d.gamma,type="l",main="発病確率")
plot(t,p.gamma,type="l",main="累積確率")
par(mfcol=c(1,1))
# ハザード関数(その時点で未発病の人に限局したとして発病率を計算)
h.gamma <- d.gamma/(1-p.gamma)
matplot(t,cbind(d.gamma,h.gamma),type="l")
legend("topleft", legend = c("発病確率", "未発病者に限った発病確率"),lty = 1:2,col=1:2)
# 累積ハザード関数
# 未発病の人が今後発病する確率の総和
H.gamma <- (k+k2-p.gamma)/(1-p.gamma)
# プロット
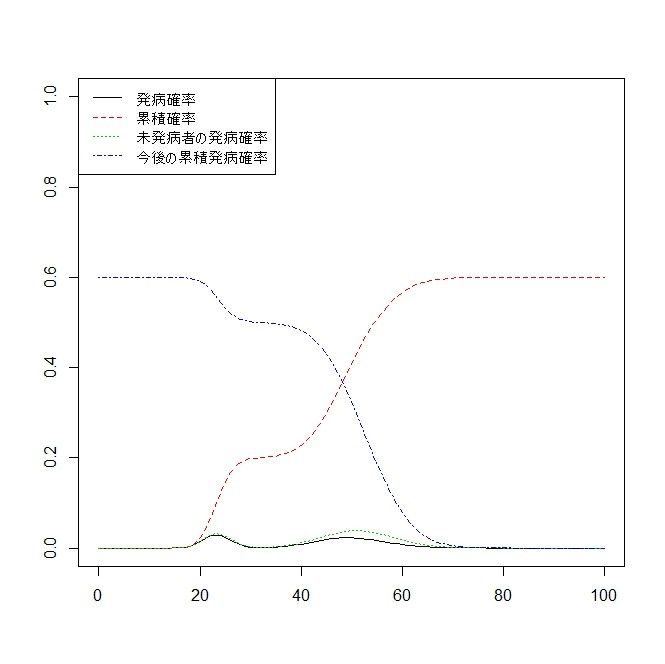
matplot(t,cbind(d.gamma,p.gamma,h.gamma,H.gamma),type="l",xlab="",ylab="",ylim=c(0,1))
legend("topleft", legend = c("発病確率", "累積確率","未発病者の発病確率","今後の累積発病確率"),lty = 1:4,col=1:4)