2014-09-13

曲線の一致を確認する

空間内にある２曲線が一致することは、２曲線上の対応する点ペアがわかっていれば、「回転」して「平行移動」させたときにすべての点が重なることで確認できる
曲線上の点の「速度ベクトル」とその微分とその微分と、さらにその微分と…、でできる複数のベクトルの列の相互関係は、回転と平行移動によって変わらない
したがってそれを比較したい
n個のベクトルがあったとき、外積代数で考えれば、 $2^n$ 個の要素の線形和を考えればよくて、そのうち、全ベクトルのウェッジ積はスカラーに戻るから、その値を算出して比較すれば、座標系の取り方に依存しなくなる
そんなことをやってみよう
ちなみに、「回転」と平行移動は、回転行列を掛けて、平行移動分を加える、という操作でもできるが、次元を一つ上げて、そのうえで、一つの行列を掛けて、その同次座標を考えてもよい
３次元の場合は、平行移動が $(m1,m2,m3)$ で、回転行列が $R=\begin{pmatrix}r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{pmatrix}$ という３ｘ３行列なら
$\begin{pmatrix}1 & 0 & 0 & 0 \\ m1 & r_{11} & r_{12} & r_{13}\\ m2 & r_{21} & r_{22} & r_{23} \\ m3 & r_{31} & r_{32} & r_{33} \end{pmatrix}$ という行列を、３次元座標 $(x_1,x_2,x_3)$ を $(1,x_1,x_2,x_3)$ に変えた上で掛け、得られた４成分ベクトルの第2,3,4成分を取り出せばよい
３次元曲線を作る

# 曲線を作ろう
# 共系変換 http://d.hatena.ne.jp/ryamada/20140907 も使って変な曲線を作る
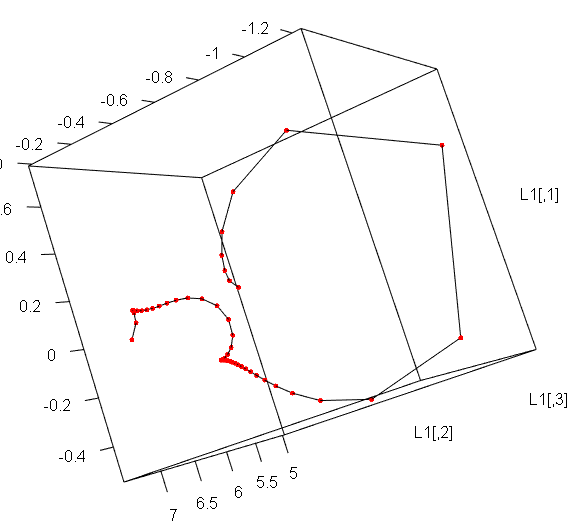
t <- seq(from=0,to=1,length=50)
ut <- (t^0.5+t^3)

L1 <- cbind(exp(0.1*ut)*cos(4*ut),exp(0.1*ut)*sin(t),exp(0.2*ut))*5
my.f <- function(X){
	z <- X[,1] + 1i*X[,2]
	new.z <- 1/z
	return(cbind(Re(new.z),Im(new.z)))
}
tmp <- my.f(L1[,1:2])
L1[,1:2] <- tmp
plot3d(L1,type="l")
points3d(L1,col=2,size=5)

回転して平行移動する

# 平行移動と回転
d <- 3 # 次元
# 回転行列
library(GPArotation)
R <- Random.Start(d)
R
# 平行移動
p.m <- rnorm(d) * (max(L1)-min(L1))*0.1
# 次元を変えずに回転して平行移動する
L2 <- t(R %*% t(L1) + p.m)
# 次元を一つ上げて１つの行列で座標変換する
M <- diag(rep(1,d+1))
M[2:(d+1),1] <- p.m
M[2:(d+1),2:(d+1)] <- R
tmp <- t(M %*% rbind(rep(1,length(t)),t(L1)))
L2.2 <- tmp[,2:(d+1)]
L2-L2.2 # ゼロ

２つの曲線を合わせてプロットしてみる

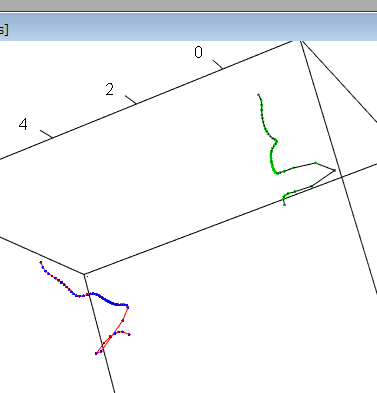
library(rgl)
L12 <- rbind(L1,L2)
L12 <- rbind(L12,rep(min(L12),3))
L12 <- rbind(L12,rep(max(L12),3))
plot3d(L12,size=0.01)
lines3d(L1,col=1)
points3d(L1,col=3,size=3)
lines3d(L2,col=2)
points3d(L2,col=4,size=3)

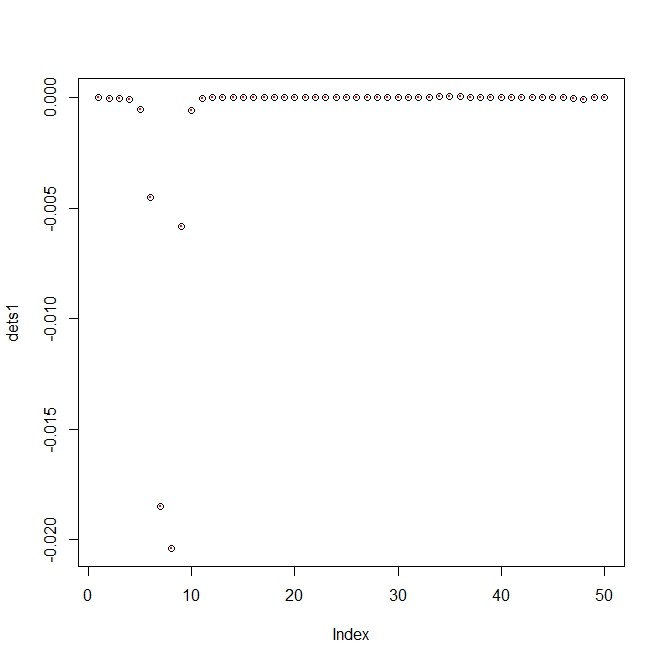
Moving Frameを計算したりして、そのうえで差分・差分の差分・・・・のベクトルのウェッジ積を計算する。ただし、それは行列の行列式にすぎない。ふたつの曲線のそれぞれの点でのその値は、すべての点のペアで一致していることをプロットして示す

mf1 <- my.Moving.Frame.2(L1) # この関数は、後に示す
mf2 <- my.Moving.Frame.2(L2)


dets2 <- dets1 <- c()
for(i in 1:length(mf1$diff.array[,1,1])){
	dets1 <- c(dets1,det(mf1$diff.array[i,,]))
	dets2 <- c(dets2,det(mf2$diff.array[i,,]))
}

plot(dets1,dets2)
abline(0,1,col=2)
plot(dets1)
points(dets2,col=2,pch=20,cex=0.5)

my.Moving.Frame.2()関数

my.Moving.Frame.2 <- function(X,k=length(X[1,])){
	n <- length(X[,1]) # No. points
	d <- length(X[1,]) # Dimension
	# inter-point distance
	L <- rep(0,n-1)
	for(i in 1:(n-1)){
		L[i] <- sqrt(sum((X[i,]-X[i+1,])^2))
	}
	diff.X <- list()
	#diff.X[[1]] <- X
	diff.X[[1]] <- apply(X,2,diff)
	diff.L <- list()
	diff.L[[1]] <- L
	for(i in 2:k){
		diff.X[[i]] <- apply(diff.X[[i-1]],2,diff)
		tmp.n.pt <- length(diff.X[[i]][,1])
		tmp.L <- rep(0,tmp.n.pt-1)
		for(j in 1:(tmp.n.pt-1)){
			tmp.L[j] <- sqrt(sum((diff.X[[i]][j,]-diff.X[[i]][j+1,])^2))
		}
		diff.L[[i]] <- tmp.L
	}
	mf <- list() # Moving Frame
	mf[[2]] <- diff.X[[2]]/sqrt(apply(diff.X[[2]]^2,1,sum))
	if(k>2){
		for(i in 3:k){
			n.pt <- length(diff.X[[i]][,1])
			ip <- apply(diff.X[[i]] * mf[[i-1]][1:n.pt,],1,sum)
			mf[[i]] <- diff.X[[i]] - ip * mf[[i-1]][1:n.pt,]
			mf[[i]] <- mf[[i]]/sqrt(apply(mf[[i]]^2,1,sum))
		}
	}
	n.pt <- length(diff.X[[k]][,1])
	mf[[1]] <- matrix(0,n.pt,d)
	for(i in 1:n.pt){
		tmp.mat <- matrix(0,d-1,d-1)
		tmp.vec <- rep(0,d-1)
		for(j in 2:d){
			tmp <- mf[[j]][i,]
			tmp.mat[j-1,] <- tmp[1:(d-1)]
			tmp.vec[j-1] <- tmp[d]
		}
		mf[[1]][i,] <- c(-solve(tmp.mat) %*% tmp.vec,1)
	}
	mf[[1]] <- mf[[1]]/sqrt(apply(mf[[1]]^2,1,sum))
	
	Cs <- matrix(0,d-1,length(diff.L[[1]]))
	for(i in 1:(d-1)){
		n.pt <- length(diff.L[[i+1]])
		Cs[i,1:n.pt] <- diff.L[[i+1]][1:n.pt]/L[1:n.pt]
	}
	mf.array <- diff.array <- array(0,c(n,k,k))
	for(i in 1:k){
		tmp.n <- length(mf[[i]][,1])
		delta.n <- n-tmp.n
		init.n <- ceiling(delta.n/2)
		if(init.n==0)init.n <- 1
		r.id <- init.n:(init.n+tmp.n-1)
		mf.array[r.id,i,] <- mf[[i]]
		
		tmp.n <- length(diff.X[[i]][,1])
		delta.n <- n-tmp.n
		init.n <- ceiling(delta.n/2)
		if(init.n==0)init.n <- 1
		r.id <- init.n:(init.n+tmp.n-1)
		diff.array[r.id,i,] <- diff.X[[i]]
	}
	
	return(list(L=L,mf=mf,mf.array=mf.array,diff.X=diff.X,diff.array=diff.array,diff.L=diff.L,Cs=Cs))
}