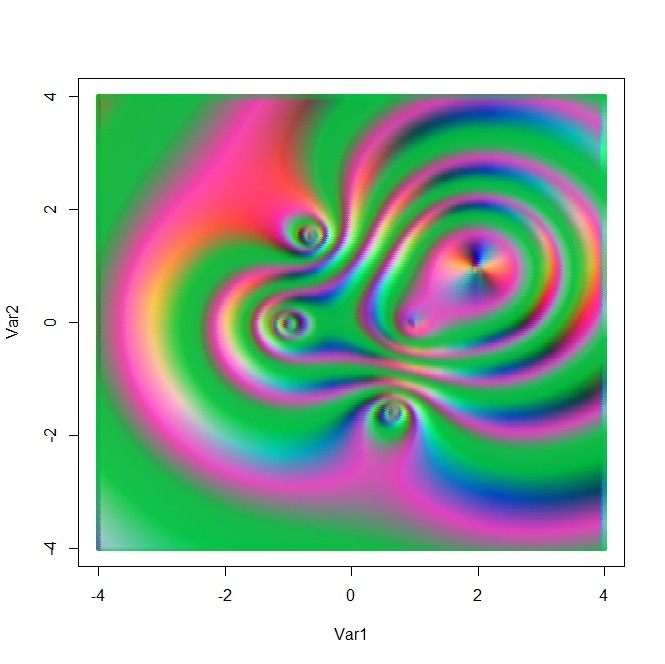
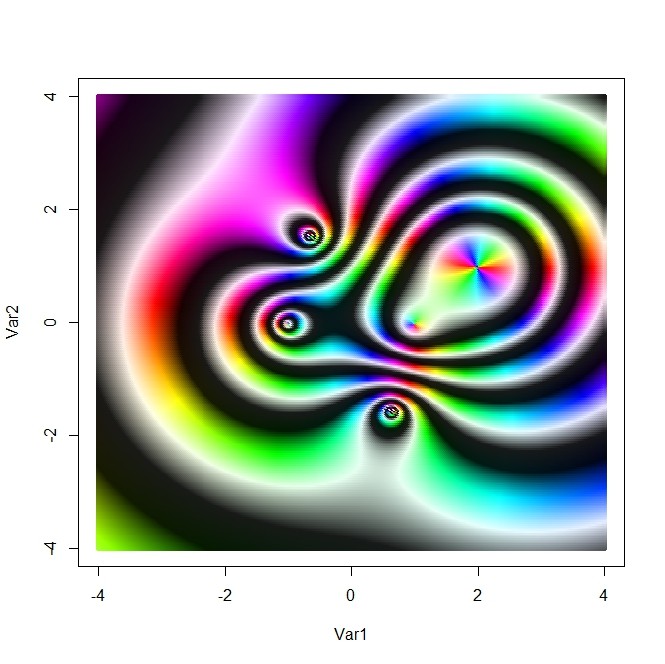
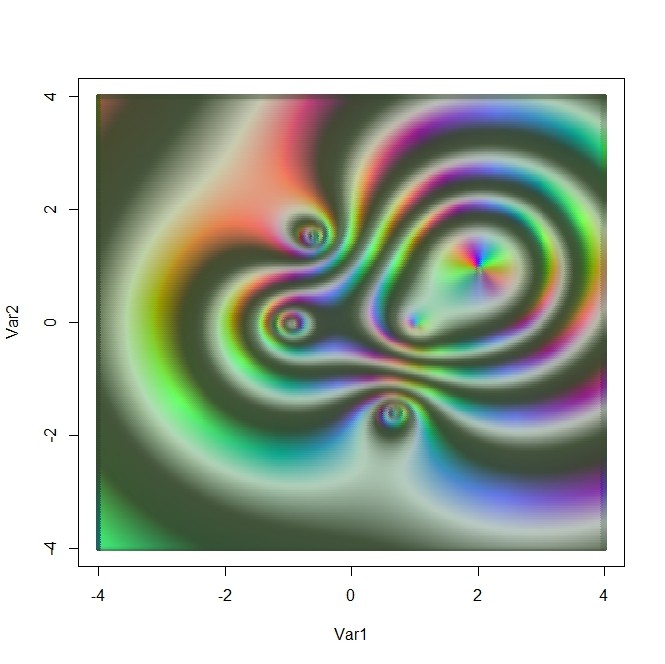
- 黒が目立つ方が原図、そうでない方が畳み込んだ図
- 原図は平面上に複素数値を与える関数を作って、複素数を三原色に対応させて描いたもの
- これに
 を左から、その共役行列フィルタを右からかけたもの(係数補正1/6もしている)
を左から、その共役行列フィルタを右からかけたもの(係数補正1/6もしている)
- アレイフィルタについてはこちらに書いたようにすることができるが、Rのonionパッケージの四元数は、Rでは一般的にベクトルや行列・アレイの要素として扱えないので、少し工夫する
- 四元数計算はベクトル的に行い、それをアレイの対応番地とともにハンドリングする
my.array.address <- function(a){
d <- dim(a)
L <- list()
L[[1]] <- 1:d[1]
for(i in 2:length(d)){
L[[i]] <- 1:d[i]
}
as.matrix(expand.grid(L))
}
a <- array(0,c(2,3,4))
my.array.address(a)
my.array.loc <- function(ad,d){
d. <- c(1,cumprod(d)[1:(length(d)-1)])
apply((t(ad)-1) * d.,2,sum)+1
}
my.array.expansion <- function(a,d1,d2=d1){
D <- dim(a)
ad <- my.array.address(a)
ad.new <- t(t(ad) + d1)
D.new <- D + d1 + d2
ret <- array(0,D.new)
tmp <- ad.new > 0
tmp2 <-t(t(ad.new) - D.new) <=0
s <- which(apply(tmp*tmp2,1,prod)==1)
loc.new <- my.array.loc(ad.new[s,],D.new)
ret[loc.new] <- a[s]
ret
}
d <- c(2,3,4)
a <- array(1:prod(d),d)
d1 <- rep(2,length(d))
d2 <- rep(3,length(d))
d1 <- c(1,1,1)
d2 <- c(2,4,2)
my.array.expansion(a,d1,d2)
my.array.filter <- function(a,f,ctr=(dim(f)+1)/2){
d.a <- dim(a)
d.f <- dim(f)
diff.d1 <- ctr-1
diff.d2 <- d.f-ctr
ad.f <- my.array.address(f)
ad.f. <- ad.f - ctr
ad.a <- my.array.address(a)
D.new <- d.a + diff.d1 + diff.d2
a.big <- array(0,D.new)
max.loc <- prod(D.new)
for(i in 1:length(ad.f.[,1])){
tmp.ad <- t(t(ad.a) + (-1)*ad.f.[i,]+diff.d1)
tmp.v <- a * f[i]
tmp.loc <- my.array.loc(tmp.ad,D.new)
s <- which(tmp.loc>0 & tmp.loc<max.loc)
a.big[tmp.loc[s]] <- a.big[tmp.loc[s]] + tmp.v[s]
}
my.array.expansion(a.big,-diff.d1,-diff.d2)
}
d <- c(2,3,4)
a <- array(1:prod(d),d)
f <- array(1,rep(3,length(d)))
a. <- my.array.filter(a,f)
a. - a
my.array.filter.q <- function(a,f,a.v = c(a),f.v = c(f),ctr=(dim(f)+1)/2,LR="L"){
d.a <- dim(a)
d.f <- dim(f)
diff.d1 <- ctr-1
diff.d2 <- d.f-ctr
ad.f <- my.array.address(f)
ad.f. <- ad.f - ctr
ad.a <- my.array.address(a)
D.new <- d.a + diff.d1 + diff.d2
a.big <- array(1:prod(D.new),D.new)
a.big.v <- quaternion(length(a.big))
max.loc <- prod(D.new)
for(i in 1:length(ad.f.[,1])){
tmp.ad <- t(t(ad.a) + (-1)*ad.f.[i,]+diff.d1)
if(LR=="L"){
tmp.v <- f.v[i] * a.v
}else if(LR=="R"){
tmp.v <- a.v * f.v[i]
}
tmp.loc <- my.array.loc(tmp.ad,D.new)
s <- which(tmp.loc>0 & tmp.loc<max.loc)
a.big.v[tmp.loc[s]] <- a.big.v[tmp.loc[s]] + tmp.v[s]
}
tmp.ad <- my.array.expansion(a.big,-diff.d1,-diff.d2)
a.big.v[c(tmp.ad)]
}
my.hsv <- function(z,int0=0.6,sat0=0.3,int1=1,sat1=1){
arg <- Arg(z)
s <- which(arg<0)
arg[s] <- arg[s]+2*pi
r <- Mod(z)
s <- which(r>1)
r[s] <- log(r[s])
r. <- 4*(r%%1)
k <- floor(r.)
r. <- r.-k
inten <- sat <- rep(0,length(r))
s <- which(k==0)
inten[s] <- int1
sat[s] <- sat1-(sat1-sat0)*r.[s]
s <- which(k==1)
inten[s] <- int1-(int1-int0)*r.[s]
sat[s] <- sat0
s <- which(k==2)
inten[s] <- int0
sat[s] <- sat1-(sat1-sat0)*(1-r.[s])
s <- which(k==3)
inten[s] <- int1-(int1-int0)*(1-r.[s])
sat[s] <- sat1
return(cbind(arg,inten,sat))
}
my.hsv2rgb <- function(h,s,v){
hi <- floor(h/(2*pi)*6)
hi[which(hi==6)] <- 0
f <- (h/(2*pi)*6) %%1
p <- v*(1-s)
q <- v *(1-f*s)
t <- v *(1-(1-f)*s)
r <- g <- b <- rep(0,length(h))
s <- which(hi==0)
r[s] <- v[s];g[s] <- t[s]; b[s] = p[s];
s <- which(hi==1)
r[s] <- q[s];g[s] <- v[s]; b[s] = p[s];
s <- which(hi==2)
r[s] <- p[s];g[s] <- v[s]; b[s] = t[s];
s <- which(hi==3)
r[s] <- p[s];g[s] <- q[s]; b[s] = v[s];
s <- which(hi==4)
r[s] <- t[s];g[s] <- p[s]; b[s] = v[s];
s <- which(hi==5)
r[s] <- v[s];g[s] <- p[s]; b[s] = q[s];
return(cbind(r,g,b))
}
x <- seq(from=-4,to=4,len=2^8)
xx <- expand.grid(x,x)
z <- xx[,1]+1i * xx[,2]
my.f <- function(z){
(z^2-1)*(z-2-1i)^2/(z^2+2+2*1i)
}
w <- my.f(z)
hsv <- my.hsv(w,int0=0.1,sat0=0.1,int1=1,sat1=1)
col <- my.hsv2rgb(hsv[,1],hsv[,3],hsv[,2])
plot(xx,pch=20,col=rgb(col[,1],col[,2],col[,3]))
col.q <- quaternion(length(col[,1]))
i(col.q) <- col[,1]
j(col.q) <- col[,2]
k(col.q) <- col[,3]
a.q <- col.q
q <- Hi
f.q <- quaternion(9)
Re(f.q) <- rep(c(1,0,Re(q)),3)
i(f.q) <- rep(c(0,0,i(q)),3)
j(f.q) <- rep(c(0,0,j(q)),3)
k(f.q) <- rep(c(0,0,k(q)),3)
f.q. <- Conj(f.q)
a=matrix(0,length(x),length(x))
f=matrix(0,3,3)
out <- my.array.filter.q(a,f,a.v = a.q,f.v = f.q,ctr=(dim(f)+1)/2,LR="L")
out2 <- my.array.filter.q(a,f,a.v = out,f.v = f.q.,ctr=(dim(f)+1)/2,LR="R")
out2 <- out2/6
R <- i(out2)
G <- j(out2)
B <- k(out2)
R <- (R-min(R))/(max(R)-min(R))
G <- (G-min(G))/(max(G)-min(G))
B <- (B-min(B))/(max(B)-min(B))
plot(xx,pch=20,col=rgb(R,G,B))
dev.new()
plot(xx,pch=20,col=rgb(col[,1],col[,2],col[,3]))
- 四元数変換のqの値をHi,Hj,Hk,(Hi+Hj+Hk)/3に変えてみると・・・
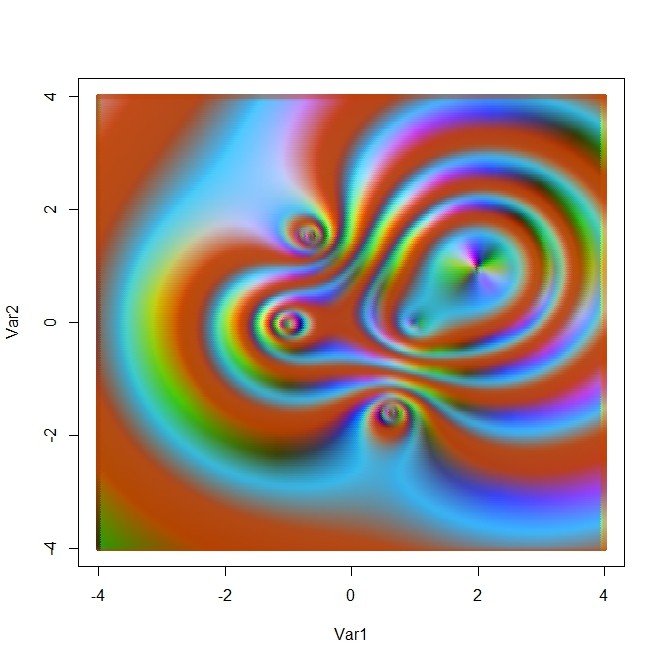
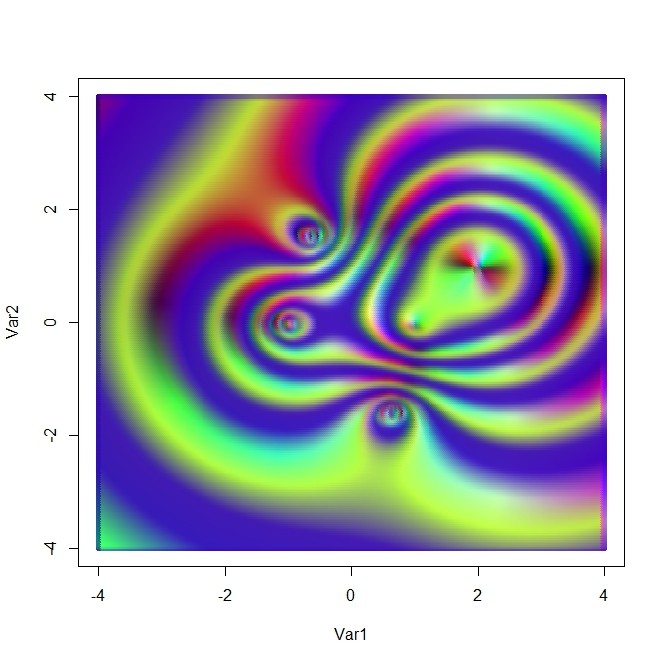
を左から、その共役行列フィルタを右からかけたもの(係数補正1/6もしている)




