ブートストラップのためのbootパッケージ - ryamadaの遺伝学・遺伝統計学メモ

信頼区間は知りたいが、計算式でだせるような単純なものでないとき、サンプルからリサンプリングすることで母集団の統計量の分布を推定するというやり方がある
Rではbootパッケージがいろいろな関数を用意している
まず、データセットがある。標本数がnで、p>=1個の測定項目がある
このnxp個の値から、色々な統計量を計算することができる
- たとえば、各測定項目の平均であったり、分散であったり、第一項目を独立変数として第二項目を従属変数とした線形回帰の係数であったり、と言ったもののことである
これらの標本データセットから計算して求める統計量は、「標本の統計量」であるが、今、知りたいのは、「母集団の統計量」である。その「母集団の統計量」の推定を分布として取り出すにあたり、標本の測定値を利用して、同じ標本数のデータセットをR回モンテカルロ発生させて、R通りの「標本統計量」を取り出すことで、それを「母集団の統計量の推定分布」としようと言うものである
データセットのモンテカルロ発生法は大きく２つに分けられる
- ノンパラメトリック法
- パラメトリック法
ノンパラメトリック法
- 基本的には、n個の標本から、n個をreplace=TRUEにてリサンプリングする。この方法をboot()関数ではオプションsim="ordinary"として指定する(デフォルト値である)
- それ以外のsimの値には"balanced", "permutation", "antithetic"があり、sim="permutation"はreplace=FALSEでのリサンプリングである。そのほかの２つについて、理解していない。"permutation"の場合には、p=1項目の単純なデータセットの場合には何も変わらないが、おそらく、第１項目はリサンプリングして、第２項目はリサンプリングしない、というようにすれば、いわゆるモンテカルロ・パーミュテーション法による統計量分布が出せる、ということだろう。boot()関数のExamplesなどにその例がないので、想像の域を出ない
- ノンパラメトリック法によるリサンプリングのやり方のバリエーションにimportance samplingがある。これは、特定の標本は多めに、特定の標本は少な目にリサンプリングし、そのうえで母集団の統計量推定を効率的に行う方法である。boot()関数で実行する場合は、sim="ordinary"とsim="balanced"の場合に対応してあり、weightsオプションで、標本の重みを指定することで実行する
- いずれにせよ、ノンパラメトリック法では、n個の標本から新たなn個の標本が作製されるが、どれが何個リサンプリングされたか、の情報の保持の仕方をboot()関数では、３通り提供している(３通りに本質的な違いはない、と思うが、１点、要確認。以下のiとfとはfの値が0以上の整数である限り、実質的に同じでしかありえないが、wの場合は、0以上のn個の実数であって、その和が1であるようなn個の実数の撮り方はi,fの方式で実現できる場合ばかりではないことに留意)
  - ３通り提供するその理由は、知りたい統計量を計算する関数をstatisticsオプションとしてboot()関数に渡さなくてはならないのだが、その関数を書く便宜上の理由と思ってよい
  - その３通りはi=indices, f=frequency, w=weightsの３つであり、それをstype=c("i","f","w")オプションで指定する。Statistics-TYPEということと思われる
  - iは、1:nの値から取り出された長さnの整数ベクトル
  - fは、長さnの整数ベクトルで、n個の標本のどれを何個取り出しているかを表す。したがって、fの和はnになる
  - wは、長さnの実数ベクトルで、n個の標本がどのくらいの割合で取り出されているかを表す。したがって、wの和は1になる
- 統計量を算出する関数(statisticsオプションに渡す関数)は、i,f,wのいずれかを引数として受け取り、それを計算に用いることで、リサンプリングごとの統計量を算出する
パラメトリック法は、パラメタによって規定される関数から乱数を発生させることでn個の標本を新たに作る。そのときのパラメタの値をn個の観測標本から指定する
- パラメトリック法の実行をする場合は、sim="parametric"とする。この場合stypeオプションは関係ない。その変わり、ran.genオプションを指定する。このran.genオプションが、パラメタで規定される乱数生成(ランダムな標本の生成)の関数である。また、mleオプションにパラメタ値を指定し、それをran.genの関数の中で使うように書く
boot()関数によって得られる統計量
- 標本観測値からp個の統計量が計算される。それがt0
- R通りのリサンプリング結果からR通りのp個の統計量が計算される。それがt
boot()関数の結果の利用
- R通りの統計量tが分布を作っているので、それがきちんとした分布になっているかを念のために確認した上で、信頼区間を出す、と言うのが、使い方の基本
- もう１つの使い方としては、t0の値がtの値のどのあたりにあるかを調べることで、仮説検定をすることもできる
boot.ci()関数による信頼区間
- R個の値から信頼区間を取り出すのに、5つの方法がある
- boot.ci()関数では、typeオプションで指定する
- typeオプションには、c("norm","basic", "stud", "perc", "bca")の5つのいずれかを指定するか、"all"を指定して５通りのすべてを返させるか、のいずれかを実施する
- 詳細をちょっと理解しきっていないが、"norm","basic","perc"の３つは、漸近的には同じもの。"norm"が得られたR個の値の分布が正規分布であることを仮定して信頼区間を決めるのに対し、"perc"はパーセンタイルベースで決める(らしい)
- 他方、"stud"と"bca"は計算量負荷を大きくしつつ、"norm","basic","perc"の３つよりも「良い感じの(その良さについての理解が不十分)」信頼区間になるようにする(らしい)。"stud"では、信頼区間を計算するに当たり、統計量自体のR通りの値と、その統計量の分散をR通り算出しておき、それを用いて統計量本体の信頼区間決定に利用する方法である
- ごく大雑把にいえば、計算負荷をかけてでも信頼区間を狭くしたくて、かつ、boot()関数での統計量計算で知りたい統計量とその分散の両方を計算するという面倒くささを避けたいなら、type="bca"とするのがよい、ということになるようだ
さて、やってみよう

library(boot)
# 適当に標本を作る
x <- rexp(100)
# 興味があるのは平均値
mean.x <- mean(x)
# boot.ci()のtype="stud"を求めるには、興味のある統計量の分散も
# ブートストラップで求める必要が必要がある
var.x <- var(x)
# stype="i" (index)の統計量関数の例
my.statistic.i <- function(x,i){
	m <- mean(x[i])
	v <- var(x[i])
	return(c(m,v))
}

out.i <- boot(data=x,statistic=my.statistic.i,R=999,stype="i")
out.i
# index=1により平均の、index=2により分散のブートストラップ結果をプロットで確認
plot(out.i,index=1)
plot(out.i,index=2)
# indexごとに信頼区間を出す
# type="stud"では第２の統計量として第１統計量の分散がないといけないので
# index=1,or 2とするとstud法が出せないとエラーが出ている
boot.ci(out.i,type="all",index=1)
boot.ci(out.i,type="all",index=2)
# ２つの統計量があり、そのindexを指定しないと、第１統計量の信頼区間が出る
# stud法の場合には第２統計量を使って第１統計量の信頼区間を出す
boot.ci(out.i,type="all")

> out.i

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = x, statistic = my.statistic.i, R = 999, stype = "i")


Bootstrap Statistics :
     original       bias    std. error
t1* 0.9874034 -0.004557424  0.09209183
t2* 0.8212310 -0.015279826  0.13755861
> plot(out.i,index=1)
> plot(out.i,index=2)
> boot.ci(out.i,type="all",index=1)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates

CALL : 
boot.ci(boot.out = out.i, type = "all", index = 1)

Intervals : 
Level      Normal              Basic         
95%   ( 0.8115,  1.1725 )   ( 0.7995,  1.1565 )  

Level     Percentile            BCa          
95%   ( 0.8183,  1.1753 )   ( 0.8255,  1.1959 )  
Calculations and Intervals on Original Scale
 警告メッセージ: 
 boot.ci(out.i, type = "all", index = 1) で: 
  bootstrap variances needed for studentized intervals
> boot.ci(out.i,type="all",index=2)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates

CALL : 
boot.ci(boot.out = out.i, type = "all", index = 2)

Intervals : 
Level      Normal              Basic         
95%   ( 0.5669,  1.1061 )   ( 0.5560,  1.0914 )  

Level     Percentile            BCa          
95%   ( 0.5511,  1.0865 )   ( 0.6017,  1.1729 )  
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable
 警告メッセージ: 
 boot.ci(out.i, type = "all", index = 2) で: 
  bootstrap variances needed for studentized intervals
> boot.ci(out.i,type="all")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates

CALL : 
boot.ci(boot.out = out.i, type = "all")

Intervals : 
Level      Normal              Basic             Studentized     
95%   ( 0.8115,  1.1725 )   ( 0.7995,  1.1565 )   ( 0.8138,  1.1830 )  

Level     Percentile            BCa          
95%   ( 0.8183,  1.1753 )   ( 0.8255,  1.1959 )  
Calculations and Intervals on Original Scale

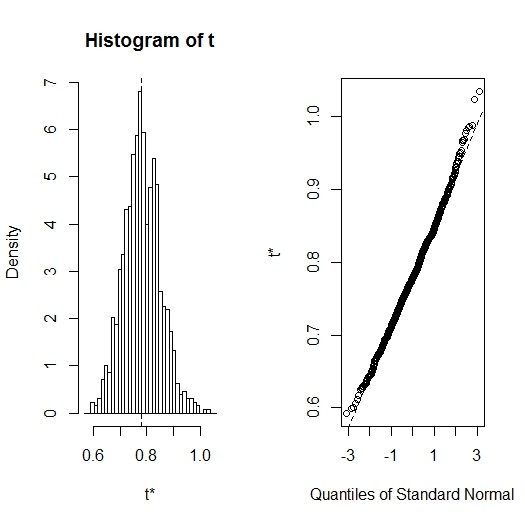
stype="f"でやってみる。ただし興味ある統計量として平均をとるが、fを使ってその分散を計算するのは面倒くさいので省略…

my.statistic.f <- function(x,f){
	m <- sum(x*f)/length(f)
	return(m)
}

out.f <- boot(data=x,statistic=my.statistic.f,R=999,stype="f")
out.f
plot(out.f)
boot.ci(out.f,type="all")

> out.f

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = x, statistic = my.statistic.f, R = 999, stype = "f")


Bootstrap Statistics :
     original        bias    std. error
t1* 0.9874034 -0.0008091503  0.09015626
> plot(out.f)
> boot.ci(out.f,type="all")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates

CALL : 
boot.ci(boot.out = out.f, type = "all")

Intervals : 
Level      Normal              Basic         
95%   ( 0.8115,  1.1649 )   ( 0.8014,  1.1636 )  

Level     Percentile            BCa          
95%   ( 0.8112,  1.1734 )   ( 0.8176,  1.1845 )  
Calculations and Intervals on Original Scale
 警告メッセージ: 
 boot.ci(out.f, type = "all") で: 
  bootstrap variances needed for studentized intervals

stype="w"でやってみる

my.statistic.w <- function(x,w){
	m <- sum(x*w)
	return(m)
}

out.w <- boot(data=x,statistic=my.statistic.w,R=999,stype="w")
out.w
plot(out.w)
boot.ci(out.w,type="all")

> out.w

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = x, statistic = my.statistic.w, R = 999, stype = "w")


Bootstrap Statistics :
     original       bias    std. error
t1* 0.9874034 0.0007187872  0.09212494
> plot(out.w)
> boot.ci(out.w,type="all")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates

CALL : 
boot.ci(boot.out = out.w, type = "all")

Intervals : 
Level      Normal              Basic         
95%   ( 0.8061,  1.1672 )   ( 0.7947,  1.1552 )  

Level     Percentile            BCa          
95%   ( 0.8196,  1.1802 )   ( 0.8289,  1.1923 )  
Calculations and Intervals on Original Scale
 警告メッセージ: 
 boot.ci(out.w, type = "all") で: 
  bootstrap variances needed for studentized intervals

あとは、boot(),boot.ci()関数のExamplesをなぞればよいだろう
bootパッケージではここで書いたboot(),boot.ci()の他、時系列データやセンサスデータに対応するブートストラップ関数もある。以下の参考資料のRnew記事などにも記載はある。Quick-Rは扱っていないし、ノンパラ法のみ
参考資料
ノンパラ法(Quick-R記事)