単調増加の検出と比較（１）
- 単調増加の検出と比較の目次
- 序
- こちらでpava()関数について書いた
- そもそも、一様増加(減少)を(発現解析のために)検出することが発端だった(こちら)
- isotonic regressionと、全順序・半順序のこと、isotonic regressionと不等式制約のこと、それが２次計画問題であること、pool adjacent violators algorithm (PAVA)は全順序の場合に限定したアルゴリズムであること、など、引用記事に頼っていたので、少し整理したい。その上で、Rのquadratic programming パッケージquadprogとその関数solve.QP()についても言及したい(こちらを参照)
- 確認事項目次
単調増加の検出と比較（２）Rのパッケージに入る前に、問題を整理しよう
- 単調増加の検出と比較の目次
- こちらが発端
- 容量反応曲線を扱っている
- 複数のデータ点があって、それが、単調減少しているかどうかの判定がしたい
- 実際には、２本の容量反応曲線があって、２本が単調減少しており、１本はもう１本の上側には来ない(等しいか下側に来る)というような関係を検出したい
単調増加の検出と比較（３）単調減少関数２本と順序・半順序について
- 単調増加の検出と比較の目次
- ある１本の容量反応曲線では、
のように
個の容量において、
と
- 単調減少である、とは[tex:\forall i,j y_i \ge y_j, x_i
- 順序と半順序(Wikiはこちら)
- １つの単調減少(増加)関係では、要素は順序を成して並んでいる
- 今、ある
の要素のすべてのペアについて大小が決まっている。このように、すべてのペアについて大小が決まって(相互に矛盾がない)とき、これを順序(または半順序と区別する意味で全順序)と言う
- 今、ある
- 半順序は？
- ２つの単調減少(増加)関係があるとする
- ２つの容量反応曲線のように
- このとき同じ
については
の大小関係が決まるが、
については、その大小関係が決まらない
を考えるとき、大小関係が決まらない値のペアがあるとき(決まらないペアはあるが、決まったペア同士に関しては矛盾がない)、半順序という
- したがって、２つの容量反応曲線があって、その関係が、片方はもう片方の下に来る、というような場合には、２本の曲線上の点全体に関して言えば、半順序を守っているが、全順序を守っているとは限らないことがわかる
- １つの単調減少(増加)関係では、要素は順序を成して並んでいる
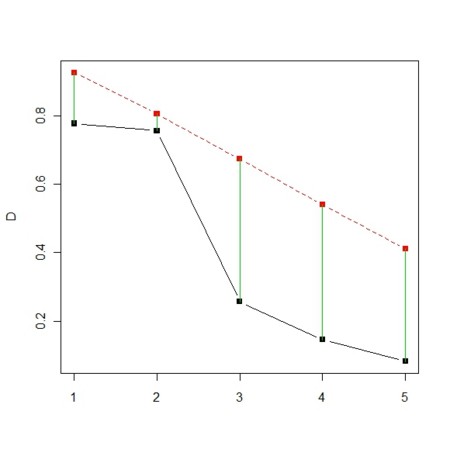
- ２本の容量反応曲線は全順序で、２本の曲線のx値を等しくする２点の大小も決まっているので、そこに辺を渡すと、これが、半順序関係
N<-5 M<-2 X<-1:N D<-matrix(runif(N*M),N,M) D<-apply(D,2,sort)[N:1,] D D<-t(apply(D,1,sort)) matplot(D,type="b",pch=15) sleep<-0.5 for(i in 1:N){ segments(i,D[i,1],i,D[i,2],col=3) Sys.sleep(sleep) }
- ここで、容量反応曲線が２本ではなくてもっとたくさんある場合も考えよう
- 例えば、ある基準となる容量反応曲線が１本あって、それとの関係を上記で作ったように満足する曲線が複数あるとする。この複数の追加曲線同士には、取り立てて関係がないとすると、次のようになる(これは、基準曲線があって、それより下にする因子が複数あり、それらの働き方が独立ならば、このようになる
- 影響を与える因子が複合的に影響量を定めるばあいについては、こちらも参考
- いずれにしても、順序・半順序が定める関係をどれとどれの間に決めるかで確定する
N<-20 M<-4 sleep<-0.2 D<-matrix(0,N,M) D[,1]<-sort(runif(N),decreasing=TRUE)+1 for(i in 2:M){ k<-0.2 D[1,i]<-D[1,1]*(runif(1)*k+(1-k)) for(j in 2:N){ D[j,i]<-min(D[j-1,i],D[j,1])*(runif(1)*k+(1-k)) } } matplot(D,type="b",pch=15) for(i in 1:N){ for(j in 2:M){ segments(i,D[i,1],i,D[i,j],col=1+j) Sys.sleep(sleep) } }
単調増加の検出と比較（４）順序・半順序と有向グラフについて
- 単調増加の検出と比較の目次
- 順序・半順序は、ペアワイズに関係が定められるかのルール
- この関係は、対称的ではない。
- 対称的ではないペアワイズな関係は、有向グラフになる
- 今、
であるときに、
から
へと向かう辺があるとすると、
をノードとする有向グラフを作ることができる
- M+1個の容量反応曲線の点を
と
とすればそれらはそれぞれ全順序関係にあるので、鎖状になる。M個の曲線は基準となる曲線と容量が相等しい点同士で結ばれる(はしごのように)。
- これをグラフオブジェクトや隣接行列で表現してみると次のようになる
N<-5 M<-3 D<-matrix(0,N,M) D[,1]<-sort(runif(N),decreasing=TRUE)+1 for(i in 2:M){ k<-0.2 D[1,i]<-D[1,1]*(runif(1)*k+(1-k)) for(j in 2:N){ D[j,i]<-min(D[j-1,i],D[j,1])*(runif(1)*k+(1-k)) } } #matplot(D,type="b",pch=15) # 隣接行列を作ってみる A<-matrix(0,(N*M),(N*M)) for(i in 1:M){ for(j in 1:(N-1)){ st<-(i-1)*N+j end<-st+1 A[st,end]<-1 } } for(i in 2:M){ st<-1:N end<-st+N*(i-1) for(j in 1:length(st)){ A[st[j],end[j]]<-1 } } A library(igraph) G<-graph.adjacency(A) plot(G,layout=layout.reingold.tilford)
単調増加の検出と比較（５）Isotonic programmingと順序・半順序について
- 単調増加の検出と比較の目次
- Isotonic regressionのWikiはこちら
- 順序・半順序にあるN個の要素に、実数
- N個の要素には順序・半順序があり、
はこの順序・半順序を満足することとする
- 実際には、N個のそれぞれの要素には、観測値が
あって、その平均が
となっていて、
- その探索の条件として
が最小になるようにする
- 順序・半順序を「サイクルのない有向グラフ」で表すこととすれば
- グラフ
はN個のノードVと、「順序・半順序」に対応する辺Eとからなるものとし
なるN個の実数集合
を見つけることである
- グラフ
- この
単調増加の検出と比較（６）Isotonic programmingとquadratic programming(２次計画)について
- 単調増加の検出と比較の目次
- ２次計画問題は、最適化問題(こちら)のうちの一つで、目的関数が2次式で定義され、制約条件の集合が一次等式と一次不等式とを合わせたものによって定義されているもの
- isotonic programming は前の記事で書いたように
- ２次計画問題であることがわかる
- ちなみに、半順序ではなく、全順序であるときには、制約がきつくなるので、より速く最適化をする方法が知られており、それ(その一つ)が pool adjacent violators algorithm (PAVA)である。
- 最小化したいのは
を最小化することに同じ
- ただし
は
を対角成分とする対角行列で、
- ただし
- これは、二次計画問題の最小化するべき関数の「一般表現
になっている
は
なので
なる連立不等式が満足されるべきであり、ここで言う
は
に対して
となるような行列
- 全順序の場合には
N<-5 Q<-matrix(0,N-1,N) for(i in 1:(N-1)){ Q[i,i]<-1 Q[i,i+1]<--1 } Q
> Q [,1] [,2] [,3] [,4] [,5] [1,] 1 -1 0 0 0 [2,] 0 1 -1 0 0 [3,] 0 0 1 -1 0 [4,] 0 0 0 1 -1
- 基準曲線が１つあって、それより下に来る曲線が複数あるときの制約条件行列は
N<-4 M<-3 D<-matrix(0,N,M) D[,1]<-sort(runif(N),decreasing=TRUE)+1 for(i in 2:M){ k<-0.2 D[1,i]<-D[1,1]*(runif(1)*k+(1-k)) for(j in 2:N){ D[j,i]<-min(D[j-1,i],D[j,1])*(runif(1)*k+(1-k)) } } matplot(D,type="b",pch=15) for(i in 1:N){ for(j in 2:M){ segments(i,D[i,1],i,D[i,j],col=1+j) } } Q<-NULL for(j in 1:M){ for(i in 1:(N-1)){ st<-(j-1)*N + i end<-st+1 tmp<-rep(0,N*M) tmp[st]<--1 tmp[end]<-1 Q<-rbind(Q,tmp) } } for(i in 2:M){ for(j in 1:N){ st<-j end<-N*(i-1)+j tmp<-rep(0,N*M) tmp[st]<--1 tmp[end]<-1 Q<-rbind(Q,tmp) } } Q
> Q [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] tmp -1 1 0 0 0 0 0 0 0 0 0 0 tmp 0 -1 1 0 0 0 0 0 0 0 0 0 tmp 0 0 -1 1 0 0 0 0 0 0 0 0 tmp 0 0 0 0 -1 1 0 0 0 0 0 0 tmp 0 0 0 0 0 -1 1 0 0 0 0 0 tmp 0 0 0 0 0 0 -1 1 0 0 0 0 tmp 0 0 0 0 0 0 0 0 -1 1 0 0 tmp 0 0 0 0 0 0 0 0 0 -1 1 0 tmp 0 0 0 0 0 0 0 0 0 0 -1 1 tmp -1 0 0 0 1 0 0 0 0 0 0 0 tmp 0 -1 0 0 0 1 0 0 0 0 0 0 tmp 0 0 -1 0 0 0 1 0 0 0 0 0 tmp 0 0 0 -1 0 0 0 1 0 0 0 0 tmp -1 0 0 0 0 0 0 0 1 0 0 0 tmp 0 -1 0 0 0 0 0 0 0 1 0 0 tmp 0 0 -1 0 0 0 0 0 0 0 1 0 tmp 0 0 0 -1 0 0 0 0 0 0 0 1
単調増加の検出と比較（７）Isotonic programming のためのRのパッケージ・関数(IsoGene,pava()とquadprog,solve.QP())について
- 単調増加の検出と比較の目次
- さて、実際にRに実装されているパッケージ・関数でやってみよう
- 最小化されるべき関数を
とする
- 制約は、
に関する等式と不等式とで表される
- 等式で表される制約meと不等式で表される制約mとがあって、併せてM=me+mとする
- 今回の例では、me=0
- 変数n、制約の個数M=mについて、M x n 行列 Amat2があって、
が制約となる
- 以降で用いるquadprogパッケージのsolve.QP()関数の場合には、等式制約と不等式制約とを両方合わせて M x n 行列にしたうえで、どれが等式制約でどれが不等式制約であるのかをプログラムに引数指定する仕組みを取っている
- データを作って
library(IsoGene) library(quadprog) # 観測用量点の数N N<-10 # M本の用量反応曲線 M<-4 # データを作ろう D<-matrix(0,N,M) D[,1]<-sort(runif(N),decreasing=TRUE)+1 for(i in 2:M){ k<-0.2 D[1,i]<-D[1,1]*(runif(1)*k+(1-k)) for(j in 2:N){ D[j,i]<-min(D[j-1,i],D[j,1])*(runif(1)*k+(1-k)) } } # データをばらつかせよう # ばらつきの係数 r<-0.3 D2<-D+rnorm(N*M,sd=sqrt(var(D))*r)
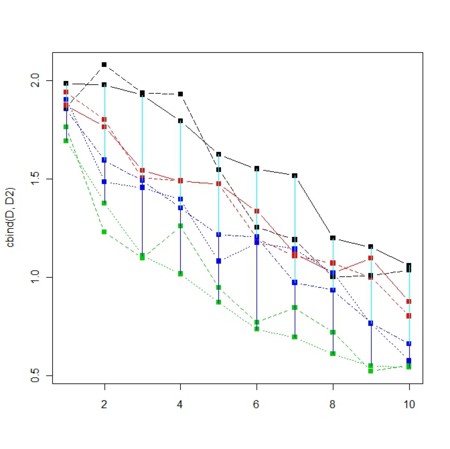
- プロットしてみる
# ばらつきを入れる前の値とばらつかせた後の値とをプロットする matplot(cbind(D,D2),type="b",pch=15,col=c(rep(1:M,2))) for(i in 1:N){ for(j in 2:M){ segments(i,D[i,1],i,D[i,j],col=1+j) } }
- Dmatはnxn正方行列で、今回の場合、
はiによらず一定なので
# Dmat # すべてtriplicateとする ws<-rep(3,N*M) Dmat<-diag(ws)
- dvecの方がデータを反映する。きれいなデータとばらつかせたデータで異なるdvec
# dvec dvec<-ws*c(D) dvec2<-ws*c(D2)
- 制約条件行列を作ろう
# Amat Q<-NULL for(j in 1:M){ for(i in 1:(N-1)){ st<-(j-1)*N + i end<-st+1 tmp<-rep(0,N*M) tmp[st]<-1 tmp[end]<--1 Q<-rbind(Q,tmp) } } for(i in 2:M){ for(j in 1:N){ st<-j end<-N*(i-1)+j tmp<-rep(0,N*M) tmp[st]<-1 tmp[end]<--1 Q<-rbind(Q,tmp) } } Q Amat2<-Q Amat<-t(Amat2)
- 制約条件のbvec
# bvec bvec<-rep(0,length(Amat[1,]))
- さて、解こう
# Dmat,dvec,Amat,bvecはそのまま # meqは制約条件のうち、等式である数。今回は0 out1<-solve.QP(Dmat,dvec,Amat,bvec=bvec,meq=0) out2<-solve.QP(Dmat,dvec2,Amat,bvec=bvec,meq=0)
- 結果
> out1 $solution [1] 1.7606338 1.5881934 1.5344888 1.4592201 1.3439146 1.2502945 1.1429360 1.0838089 1.0694384 1.0424076 [11] 1.7213358 1.5009083 1.4585956 1.4119514 1.1144510 0.9078028 0.7854388 0.6350420 0.6181277 0.6076870 [21] 1.4162341 1.2329624 1.1962830 1.1570695 1.0061177 0.8408625 0.8052883 0.6720841 0.5707691 0.4617527 [31] 1.4228720 1.2459309 1.1158810 1.0977527 0.9282307 0.8692899 0.7723391 0.7202274 0.5788950 0.4863466 $value [1] -25.17345 $unconstrained.solution [1] 1.7606338 1.5881934 1.5344888 1.4592201 1.3439146 1.2502945 1.1429360 1.0838089 1.0694384 1.0424076 [11] 1.7213358 1.5009083 1.4585956 1.4119514 1.1144510 0.9078028 0.7854388 0.6350420 0.6181277 0.6076870 [21] 1.4162341 1.2329624 1.1962830 1.1570695 1.0061177 0.8408625 0.8052883 0.6720841 0.5707691 0.4617527 [31] 1.4228720 1.2459309 1.1158810 1.0977527 0.9282307 0.8692899 0.7723391 0.7202274 0.5788950 0.4863466 $iterations [1] 1 0 $Lagrangian [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [52] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 $iact [1] 0 > > out2 $solution [1] 1.8479498 1.5062915 1.5062915 1.4910746 1.3453317 1.1982639 1.0845460 1.0845460 1.0845460 1.0845460 [11] 1.7073539 1.5062915 1.5062915 1.4519923 0.9273577 0.9273577 0.7169679 0.7169679 0.6646322 0.6646322 [21] 1.2745786 1.2606716 1.2606716 1.2606716 0.9175620 0.9175620 0.9175620 0.6482105 0.6482105 0.6482105 [31] 1.2877883 1.1185829 1.0685545 0.9041312 0.8946122 0.8946122 0.7074181 0.7074181 0.5164071 0.4327213 $value [1] -24.71127 $unconstrained.solution [1] 1.8479498 1.4801033 1.4579306 1.4910746 1.3453317 1.1982639 1.0813759 1.0341926 0.9415810 1.2810346 [11] 1.7073539 1.5149246 1.5722076 1.4519923 0.8326514 1.0220641 0.7111795 0.7227562 0.6261859 0.7030785 [21] 1.2745786 1.1908582 1.2852327 1.3059240 0.8881577 0.9410679 0.9234605 0.6031618 0.6830170 0.6584525 [31] 1.2877883 1.1185829 1.0685545 0.9041312 0.8199964 0.9692281 0.6990717 0.7157646 0.5164071 0.4327213 $iterations [1] 18 0 $Lagrangian [1] 0.000000000 0.017555148 0.000000000 0.000000000 0.000000000 0.000000000 0.003170138 0.053523534 [9] 0.196488559 0.000000000 0.000000000 0.000000000 0.000000000 0.094706353 0.000000000 0.005788359 [17] 0.000000000 0.038446317 0.000000000 0.069813443 0.045252374 0.000000000 0.029404307 0.005898483 [25] 0.000000000 0.045048638 0.010242070 0.000000000 0.000000000 0.000000000 0.000000000 0.074615838 [33] 0.000000000 0.008346482 0.000000000 0.000000000 0.000000000 0.008633070 0.065916062 0.000000000 [41] 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 [49] 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 [57] 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 [65] 0.000000000 0.000000000 $iact [1] 9 14 32 39 20 26 8 18 21 23 2 34 27 16 38 24 7
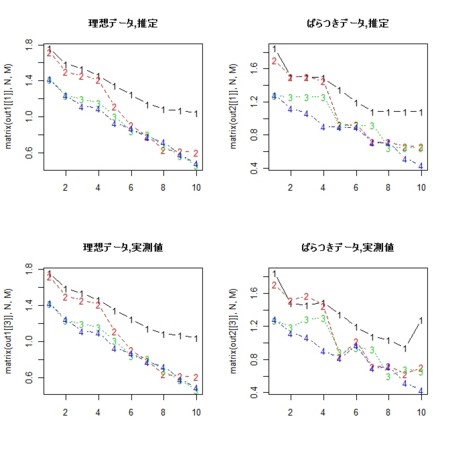
- それをプロット(ばらつきを入れる前のデータと入れた後のデータのそれぞれについて、推測グラフと実測値グラフ)
par(mfcol=c(2,2)) matplot(matrix(out1[[1]],N,M),type="b",main="理想データ,推定") matplot(matrix(out1[[3]],N,M),type="b",main="理想データ,実測値") matplot(matrix(out2[[1]],N,M),type="b",main="ばらつきデータ,推定") matplot(matrix(out2[[3]],N,M),type="b",main="ばらつきデータ,実測値") par(mfcol=c(1,1))
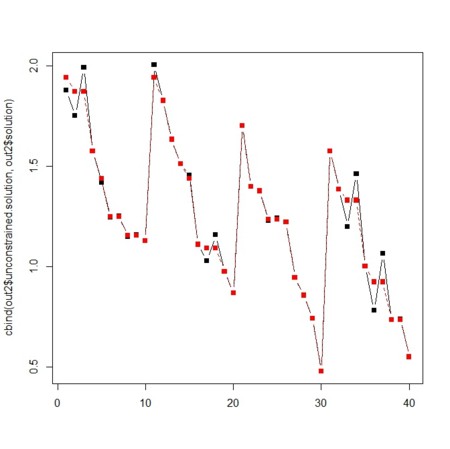
- 推定結果と実測値をプロットする
matplot(cbind(out1$unconstrained.solution,out1$solution),type="b",pch=15,col=c(rep(1:M,2))) matplot(cbind(out2$unconstrained.solution,out2$solution),type="b",pch=15,col=c(rep(1:M,2)))
単調増加の検出と比較（８）Isotonic programming回帰結果の評価について
- 単調増加の検出と比較の目次
- 前までの記事で、単調減少(増加)へのあてはめが、順序・半順序を問わずできるようになった
- さて、これを、多件数に実施して、それらを一塊として評価することを考えよう
- IsoGeneパッケージは、「順序」の場合のIsotonic programmingをした上で、その当て嵌まりの良さを評価し、多件数で実行する仕組みである
- IsoGene1()関数の中身を見る
library(IsoGene) IsoGene1
- とすれば中身が見える(日本語コメントは、この記事のために書き込んだもの)
> IsoGene1 function (x, y) { ordx <- order(x) x <- x[ordx] y <- y[ordx] unx <- unique(x) n.p <- table(x) n.g <- length(n.p) # 群ごとの平均 y.m <- tapply(y, as.factor(x), mean) y.m.tot <- rep(mean(y), length(unx)) y.is.u <- pava(y = y.m, w = n.p) y.is.d <- pava(y = y.m, w = n.p, decreasing = TRUE) # ここまでが、pava()関数を用いた、『Isotonic modelへの当て嵌め』 # 以降が、実測データと当て嵌め値とのずれを数値化する部分 # u,d, up/dnがup,downを表す # u/dの向きが決まっていれば、この区別は不要になる iso.u <- rep.iso.u <- rep.iso.d <- y.m.all <- NULL rep.iso.d <- rep(y.is.d, n.p) rep.iso.u <- rep(y.is.u, n.p) y.m.all <- rep(y.m, n.p) # 全レコードの平方和(すべてのレコードで同じ値が返ってくるとしたら…) SST0 <- sum((y - mean(y))^2) # up/downモデルからのずれの平方和 SSIS.u1 <- sum((rep.iso.u - y)^2) SSIS.d1 <- sum((rep.iso.d - y)^2) # 群ごとの平均とレコードとの作る平方和 SST <- sum((y - y.m.all)^2) direction <- if (SSIS.u1 <= SSIS.d1) "u" else "d" # 以下は５つの方法のそれぞれの流儀で値を算出 lambda1.up <- SSIS.u1/SST0 Esquare.up <- 1 - lambda1.up iso.u <- y.is.u w.up <- (y.is.u[n.g] - y.m[1])/sqrt(sum((y - y.m.all)^2)/(sum(n.p) - n.g) * (1/n.p[1] + 1/n.p[n.g])) w.c.up <- (y.is.u[n.g] - y.is.u[1])/sqrt(sum((y - y.m.all)^2)/(sum(n.p) - n.g) * (1/n.p[1] + 1/n.p[n.g])) m.up <- (y.is.u[n.g] - y.is.u[1])/sqrt(SSIS.u1/(sum(n.p) - n.g)) i.up <- (y.is.u[n.g] - y.is.u[1])/sqrt(SSIS.u1/(sum(n.p) - length(unique(y.is.u)))) lambda1.dn <- SSIS.d1/SST0 Esquare.dn <- 1 - lambda1.dn iso.u <- y.is.d w.dn <- (y.is.d[n.g] - y.m[1])/sqrt(sum((y - y.m.all)^2)/(sum(n.p) - n.g) * (1/n.p[1] + 1/n.p[n.g])) w.c.dn <- (y.is.d[n.g] - y.is.d[1])/sqrt(sum((y - y.m.all)^2)/(sum(n.p) - n.g) * (1/n.p[1] + 1/n.p[n.g])) m.dn <- (y.is.d[n.g] - y.is.d[1])/sqrt(SSIS.d1/(sum(n.p) - n.g)) i.dn <- (y.is.d[n.g] - y.is.d[1])/sqrt(SSIS.d1/(sum(n.p) - length(unique(y.is.d)))) res <- list(E2.up = Esquare.up, Williams.up = as.numeric(w.up), Marcus.up = as.numeric(w.c.up), M.up = as.numeric(m.up), ModM.up = as.numeric(i.up), E2.dn = Esquare.dn, Williams.dn = as.numeric(w.dn), Marcus.dn = as.numeric(w.c.dn), M.dn = as.numeric(m.dn), ModM.dn = as.numeric(i.dn), direction = direction) return(res) } <environment: namespace:IsoGene>
