修理する８ 「イベント・修理曲面」上に描く曲線

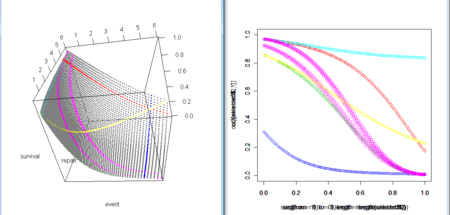
• イベントと修理が確率的に起きているとき、累積してフェノタイプに影響を与える確率が３次元空間中の曲面で表された
• ここで、イベント生起確率・修理確率に濃度依存的に影響を与える物質があり、その濃度-サバイバル関係を調べるということは、その物質が濃度別に、この曲面のどこにあたるかをとり、その軌跡を取り出すことになる

# 修復ありポアッソン


matrixA<-function(p,q,n,open=FALSE){
	k<-p
	h<-q
	N<-n
	M<-matrix(0,N,N)

	M[1,1]<--k
	M[1,2]<-h
	M[2,1]<-k
	M[2,2]<--(k+h)
	M[2,3]<-h

	for(i in 2:(N-1)){
		M[i,i-1]<-k
		M[i,i]<--(k+h)
		M[i,i+1]<-h
	}

	M[N,N-1]<-k
	if(open){
		M[N,N]<--(k+h)
	}else{
		M[N,N]<--h
	}
	
	M
}


my.ShokiChi<-function(A,v0,t){
	n<-length(v0)
	# 固有値分解
	eigen.out<-eigen(A)
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(eigen.out[[1]])
	# 計算する
	x<-t
	Ys<-matrix(0,length(x),n)
	# 初期値も適当に
	Ys0<-v0
	for(i in 1:(length(x))){
		Bex<-diag(exp(eigen.out[[1]]*x[i]))
		#Aex<-V%*%Bex%*%U
		#Ys[i,]<-Aex%*%Ys0
		Ys[i,]<-V%*%(Bex%*%(U%*%Ys0))
		#print(Ys[i,])
	}
	ReYs<-Re(Ys)
	ReYs[which(ReYs<0)]<-0
	#print(range(ReYs))
	ReYs
}


# pは単位時間あたりの平均イベント生起回数
# qは単位時間当たりの平均修復イベント生起回数

# pとqとを与えて、「得点」が閾値以下である確率を求める

Syufuku.Poisson<-function(p,q,n,maxk=NULL,t=1,open=FALSE){
	k<-0:n
	if(!is.null(maxk)){
		k<-0:maxk
	}
	ret<-rep(0,length(k))
	if(p==0){
		if(q==0){
			ret<-rep(-1,length(k))
			
		}else{
			ret[which(k>=0)]<-1
		}
	}else{
		if(q==0){
			ret<-ppois(k,p*t)
			#print((ret))
		}else{
			A<-matrixA(p=p,q=q,n=n,open=open)
			v0<-c(1,rep(0,n-1))
			my.out<-my.ShokiChi(A,v0,t)
			ret<-cumsum(my.out)
			#print(range(ret))
		}
	}
	ret
}

################

t<-1
#kq<-2^(seq(from=-1,to=1,length=20))
maxPQ<-6
#kq<-seq(from=1,to=maxPQ,by=0.1)
kq<-exp(seq(from=-log(maxPQ),to=log(maxPQ),length=100))
kp<-kq
q<-kq
p<-kp
n<-20
maxk<-10

pqt<-expand.grid(p,q,t)
#out<-rep(0,length(pqt[,1]))
out<-matrix(0,length(pqt[,1]),maxk)
for(i in 1:length(pqt[,1])){
	#A<-matrixA(pqt[i,1],pqt[i,2],n)
	#print(A)
	out[i,]<-Syufuku.Poisson(p=pqt[i,1],q=pqt[i,2],t=pqt[i,3],n=n)[1:maxk]
}

#plot(pqt)


library(rgl)
plot3d(log(pqt[,1]),log(pqt[,2]),out[,1],zlim=c(0,1))
plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1))
points3d(pqt[,1],pqt[,2],out[,2],col=2)

plot3d(log(pqt[,1]),log(pqt[,2]),out[,1],type="l",zlim=c(0,1))

plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1))

for(i in 2:maxk){
	points3d(pqt[,1],pqt[,2],out[,i],col=i)

}

# 出力を使っていくつか考える
col<-rep(gray(0.5),length(pqt[,1]))
# 修復力が大きいときに、濃度依存的にイベントが増える場合
selected1 <- which(pqt[,2]==q[length(q)-5])
# 修復力が小さいときに、濃度依存的にイベントが増える場合
selected2 <- which(pqt[,2]==q[5])
# イベント頻度が高いときに、濃度依存的に修復が弱まる場合
selected3 <- which(pqt[,1]==p[length(p)-5])
# イベント頻度が低いときに、濃度依存的に修復が弱まる場合
selected4 <- which(pqt[,1]==p[5])
# 濃度依存的にイベントが増え、修復が弱まる場合
#selected5 <- which(pqt[,1]+pqt[,2]==maxPQ/2)
selected5 <- which(abs(log(pqt[,1])+log(pqt[,2])-1)<0.05)
selected5.2 <- which(abs(log(pqt[,1])+log(pqt[,2]))<0.05)
# 濃度依存的にイベントが増え、修復が強まる場合
selected6 <- which(pqt[,1]==pqt[,2])

col[selected1]<-2
col[selected2]<-3
col[selected3]<-4
col[selected4]<-5
col[selected5]<-6
col[selected5.2]<-6
col[selected6]<-7

plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1),col=col,cex=0.01,xlab="event",ylab="repair",zlab="survival")


#plot(pqt[selected1,1],out[selected1,1],col=2,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=0,to=1,length=length(selected1)),out[selected1,1],col=2,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected2,1],out[selected2,1],col=3,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=0,to=1,length=length(selected2)),out[selected2,1],col=3,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected3[length(selected3):1],2],out[selected3,1],col=4,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=1,to=0,length=length(selected3)),out[selected3,1],col=4,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
plot(seq(from=1,to=0,length=length(selected4)),out[selected4,1],col=5,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected5,1],out[selected5,1],col=6,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=1,to=0,length=length(selected5)),out[selected5,1],col=6,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
plot(seq(from=1,to=0,length=length(selected5.2)),out[selected5.2,1],col=6,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected6,1],out[selected6,1],col=7,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=0,to=1,length=length(selected6)),out[selected6,1],col=7,xlim=c(0,1),ylim=c(0,1))

• 上のソースは濃度を指数関数的に変化させたもの
• 下のソースは濃度を等間隔で変化させたもの

# 修復ありポアッソン


matrixA<-function(p,q,n,open=FALSE){
	k<-p
	h<-q
	N<-n
	M<-matrix(0,N,N)

	M[1,1]<--k
	M[1,2]<-h
	M[2,1]<-k
	M[2,2]<--(k+h)
	M[2,3]<-h

	for(i in 2:(N-1)){
		M[i,i-1]<-k
		M[i,i]<--(k+h)
		M[i,i+1]<-h
	}

	M[N,N-1]<-k
	if(open){
		M[N,N]<--(k+h)
	}else{
		M[N,N]<--h
	}
	
	M
}


my.ShokiChi<-function(A,v0,t){
	n<-length(v0)
	# 固有値分解
	eigen.out<-eigen(A)
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(eigen.out[[1]])
	# 計算する
	x<-t
	Ys<-matrix(0,length(x),n)
	# 初期値も適当に
	Ys0<-v0
	for(i in 1:(length(x))){
		Bex<-diag(exp(eigen.out[[1]]*x[i]))
		#Aex<-V%*%Bex%*%U
		#Ys[i,]<-Aex%*%Ys0
		Ys[i,]<-V%*%(Bex%*%(U%*%Ys0))
		#print(Ys[i,])
	}
	ReYs<-Re(Ys)
	ReYs[which(ReYs<0)]<-0
	#print(range(ReYs))
	ReYs
}


# pは単位時間あたりの平均イベント生起回数
# qは単位時間当たりの平均修復イベント生起回数

# pとqとを与えて、「得点」が閾値以下である確率を求める

Syufuku.Poisson<-function(p,q,n,maxk=NULL,t=1,open=FALSE){
	k<-0:n
	if(!is.null(maxk)){
		k<-0:maxk
	}
	ret<-rep(0,length(k))
	if(p==0){
		if(q==0){
			ret<-rep(-1,length(k))
			
		}else{
			ret[which(k>=0)]<-1
		}
	}else{
		if(q==0){
			ret<-ppois(k,p*t)
			#print((ret))
		}else{
			A<-matrixA(p=p,q=q,n=n,open=open)
			v0<-c(1,rep(0,n-1))
			my.out<-my.ShokiChi(A,v0,t)
			ret<-cumsum(my.out)
			#print(range(ret))
		}
	}
	ret
}

################

t<-1
#kq<-2^(seq(from=-1,to=1,length=20))
maxPQ<-40
kq<-seq(from=1,to=maxPQ,by=0.1)
kp<-kq
q<-kq
p<-kp
n<-20
maxk<-10

pqt<-expand.grid(p,q,t)
#out<-rep(0,length(pqt[,1]))
out<-matrix(0,length(pqt[,1]),maxk)
for(i in 1:length(pqt[,1])){
	#A<-matrixA(pqt[i,1],pqt[i,2],n)
	#print(A)
	out[i,]<-Syufuku.Poisson(p=pqt[i,1],q=pqt[i,2],t=pqt[i,3],n=n)[1:maxk]
}

#plot(pqt)


library(rgl)
plot3d(log(pqt[,1]),log(pqt[,2]),out[,1],zlim=c(0,1))
plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1))
points3d(pqt[,1],pqt[,2],out[,2],col=2)

plot3d(log(pqt[,1]),log(pqt[,2]),out[,1],type="l",zlim=c(0,1))

plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1))

for(i in 2:maxk){
	points3d(pqt[,1],pqt[,2],out[,i],col=i)

}

# 出力を使っていくつか考える
col<-rep(gray(0.5),length(pqt[,1]))
# 修復力が大きいときに、濃度依存的にイベントが増える場合
selected1 <- which(pqt[,2]==q[length(q)-5])
# 修復力が小さいときに、濃度依存的にイベントが増える場合
selected2 <- which(pqt[,2]==q[5])
# イベント頻度が高いときに、濃度依存的に修復が弱まる場合
selected3 <- which(pqt[,1]==p[length(p)-5])
# イベント頻度が低いときに、濃度依存的に修復が弱まる場合
selected4 <- which(pqt[,1]==p[5])
# 濃度依存的にイベントが増え、修復が弱まる場合
selected5 <- which(pqt[,1]+pqt[,2]==maxPQ/2)
# 濃度依存的にイベントが増え、修復が強まる場合
selected6 <- which(pqt[,1]==pqt[,2])

col[selected1]<-2
col[selected2]<-3
col[selected3]<-4
col[selected4]<-5
col[selected5]<-6
col[selected6]<-7

plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1),col=col,cex=0.01,xlab="event",ylab="repair",zlab="survival")


plot(pqt[selected1,1],out[selected1,1],col=2,xlim=range(pqt[,1]),ylim=c(0,1))
par(new=TRUE)
plot(pqt[selected2,1],out[selected2,1],col=3,xlim=range(pqt[,1]),ylim=c(0,1))
par(new=TRUE)
plot(pqt[selected3[length(selected3):1],2],out[selected3,1],col=4,xlim=range(pqt[,1]),ylim=c(0,1))
par(new=TRUE)
plot(pqt[selected4[length(selected4):1],2],out[selected4,1],col=5,xlim=range(pqt[,1]),ylim=c(0,1))
par(new=TRUE)
plot(pqt[selected5,1],out[selected5,1],col=6,xlim=range(pqt[,1]),ylim=c(0,1))
par(new=TRUE)
plot(pqt[selected6,1],out[selected6,1],col=7,xlim=range(pqt[,1]),ylim=c(0,1))