１１ 定常状態

• 定常状態になっているとして、どういう分布になっているかを考えてみる
• 状態はのように、片方が閉じた離散的１次元空間
• そこに微分係数行列が
  • 
• 定常状態においては、状態に関してとなる。
• これを解いていく
  • 
  • 
  • 
  • ...
  • 第１式から、
  • 第２式をから、
  • ここから、が、この(無限)連立方程式の解であることが確かめられる
• ここでであるからとなる
• と置けば、が得られる
• のときとなって
  • 
• のときには
• のときには、収束せず、状態空間の値の大きい方へと発散する

Teijo<-function(p,q,n,N=NULL){
	S<-0
	ret<-rep(0,n+1)

	if(p<q){
		if(is.null(N)){
			S<-q/(q-p)
		}else{
			S<-q/(q-p)+(p/q)^N*p/(p-q)
		}
		ret<-(p/q)^(0:n)/S
	}else if(p==q){
		if(is.null(N)){
			
		}else{
			ret<-rep(1/(N+1),n+1)
		}
		
	}else{
		if(is.null(N)){
			
		}else{
			S<-q/(q-p)+(p/q)^N*p/(p-q)
			ret<-(p/q)^(0:n)/S
		}
	}
	ret
}

ps<-qs<-seq(from=0.5,to=2,by=0.02)
pq<-expand.grid(ps,qs)
n<-10
N<-20
out<-matrix(0,length(pq[,1]),n+1)
for(i in 1:length(pq[,1])){
	out[i,]<-Teijo(pq[i,1],pq[i,2],n,N)
}

library(rgl)
plot3d(pq[,1],pq[,2],apply(out[,1:10],1,sum))

for(i in 2:(n+1)){
	 plot3d(pq[,1],pq[,2],apply(out[,1:i],1,sum))
	Sys.sleep(1)
}

plot3d(pq[,1],pq[,2],apply(out[,1:2],1,sum))
plot3d(pq[,1],pq[,2],apply(out[,1:20],1,sum))

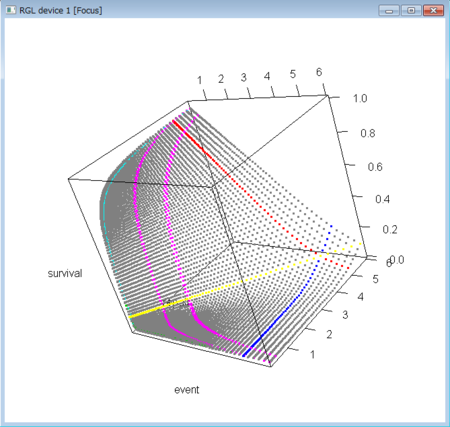
• この定常状態を用いても、固有値を求めて求めた値と同様のパターンを作れることがわかる

t<-1
#kq<-2^(seq(from=-1,to=1,length=20))
maxPQ<-6
#kq<-seq(from=1,to=maxPQ,by=0.1)
kq<-exp(seq(from=-log(maxPQ),to=log(maxPQ),length=100))
kp<-kq
q<-kq
p<-kp
n<-20
maxk<-10

pqt<-expand.grid(p,q,t)
#out<-rep(0,length(pqt[,1]))
out<-matrix(0,length(pqt[,1]),maxk)
for(i in 1:length(pqt[,1])){
	#A<-matrixA(pqt[i,1],pqt[i,2],n)
	#print(A)
	#out[i,]<-Syufuku.Poisson(p=pqt[i,1],q=pqt[i,2],t=pqt[i,3],n=n)[1:maxk]
	out[i,]<-cumsum(Teijo(p=pqt[i,1],q=pqt[i,2],n=n,N=maxk)[1:maxk])
}

#plot(pqt)


library(rgl)
plot3d(log(pqt[,1]),log(pqt[,2]),out[,1],zlim=c(0,1))
plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1))
points3d(pqt[,1],pqt[,2],out[,2],col=2)

plot3d(log(pqt[,1]),log(pqt[,2]),out[,1],type="l",zlim=c(0,1))

plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1))

for(i in 2:maxk){
	points3d(pqt[,1],pqt[,2],out[,i],col=i)

}

# 出力を使っていくつか考える
col<-rep(gray(0.5),length(pqt[,1]))
# 修復力が大きいときに、濃度依存的にイベントが増える場合
selected1 <- which(pqt[,2]==q[length(q)-5])
# 修復力が小さいときに、濃度依存的にイベントが増える場合
selected2 <- which(pqt[,2]==q[5])
# イベント頻度が高いときに、濃度依存的に修復が弱まる場合
selected3 <- which(pqt[,1]==p[length(p)-5])
# イベント頻度が低いときに、濃度依存的に修復が弱まる場合
selected4 <- which(pqt[,1]==p[5])
# 濃度依存的にイベントが増え、修復が弱まる場合
#selected5 <- which(pqt[,1]+pqt[,2]==maxPQ/2)
selected5 <- which(abs(log(pqt[,1])+log(pqt[,2])-1)<0.05)
selected5.2 <- which(abs(log(pqt[,1])+log(pqt[,2]))<0.05)
# 濃度依存的にイベントが増え、修復が強まる場合
selected6 <- which(pqt[,1]==pqt[,2])

col[selected1]<-2
col[selected2]<-3
col[selected3]<-4
col[selected4]<-5
col[selected5]<-6
col[selected5.2]<-6
col[selected6]<-7

plot3d(pqt[,1],pqt[,2],out[,1],zlim=c(0,1),col=col,cex=0.01,xlab="event",ylab="repair",zlab="survival")


#plot(pqt[selected1,1],out[selected1,1],col=2,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=0,to=1,length=length(selected1)),out[selected1,1],col=2,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected2,1],out[selected2,1],col=3,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=0,to=1,length=length(selected2)),out[selected2,1],col=3,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected3[length(selected3):1],2],out[selected3,1],col=4,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=1,to=0,length=length(selected3)),out[selected3,1],col=4,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
plot(seq(from=1,to=0,length=length(selected4)),out[selected4,1],col=5,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected5,1],out[selected5,1],col=6,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=1,to=0,length=length(selected5)),out[selected5,1],col=6,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
plot(seq(from=1,to=0,length=length(selected5.2)),out[selected5.2,1],col=6,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
#plot(pqt[selected6,1],out[selected6,1],col=7,xlim=range(pqt[,1]),ylim=c(0,1))
plot(seq(from=0,to=1,length=length(selected6)),out[selected6,1],col=7,xlim=c(0,1),ylim=c(0,1))