ばらばらなこと - ryamadaの遺伝学・遺伝統計学メモ

こちらで「ばらばらなこと」をかいつまんで伝える指標として、Rのcor()関数を使う話しをしている
「(スカラーな)指標」なので、全体の情報のある一面をかいつまんでいる
確かに「ばらばら」なことを表せるけれども、「一面」だから、「ある面でのばらばら」を表している
別の面のばらばらでないことは、表していない
別の面のばらばらを見落とさないための工夫が必要になる
ばらばらなような、ばらばらでないような２変数をいくつか見てみよう
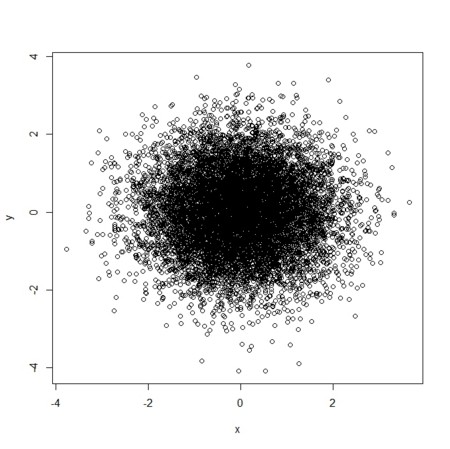
２変数がそれぞれ正規分布からの乱数のとき

N<-10000
x<-rnorm(N)
y<-rnorm(N)
plot(x,y)
cor(x,y)

> cor(x,y)
[1] -0.003402283

２変数がそれぞれ一様分布からの乱数のとき

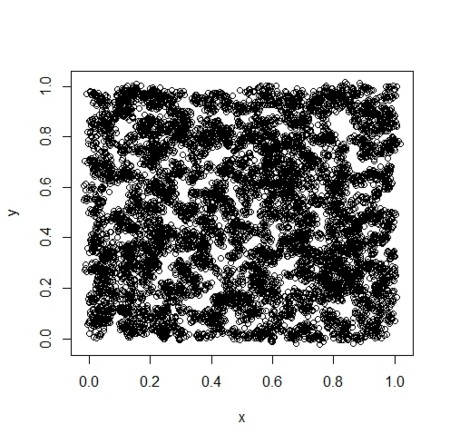
N<-10000
x<-runif(N)
y<-runif(N)
plot(x,y)
cor(x,y)

> cor(x,y)
[1] 0.01228287

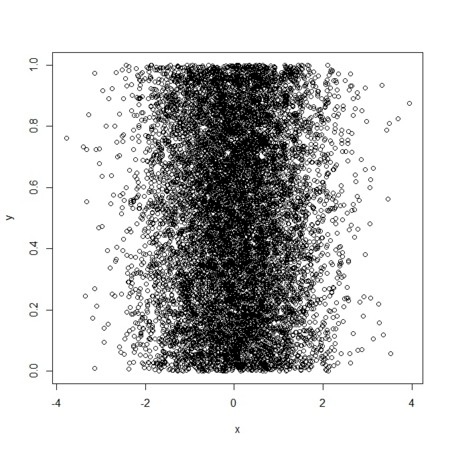
２変数の片方が正規分布から、もう片方が一様分布からの乱数のとき

N<-10000
x<-rnorm(N)
y<-runif(N)
plot(x,y)
cor(x,y)

> cor(x,y)
[1] 0.001475063

ばらばらかと思っても、ヒエラルキーがあるとき

N<-1000

xcore<-runif(N)
ycore<-runif(N)
x<-y<-c()
for(i in 1:N){
	x<-c(x,rnorm(10,sd=0.01)+xcore[i])
	y<-c(y,rnorm(10,sd=0.01)+ycore[i])
}
plot(x,y)
cor(x,y)

> cor(x,y)
[1] -0.003911722

２変数が相互作用があって周回関係にあるとき

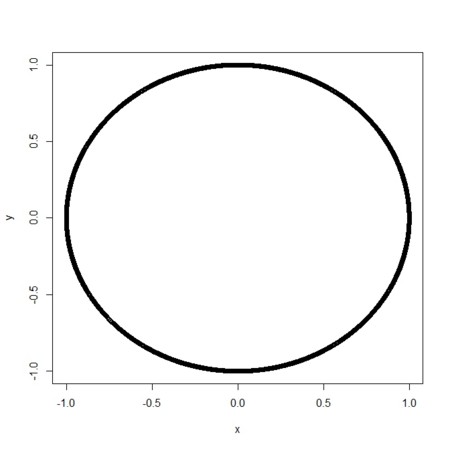
t<-runif(n)*2*pi
x<-sin(t)
y<-cos(t)
plot(x,y)
cor(x,y)

> cor(x,y)
[1] 0.002137791

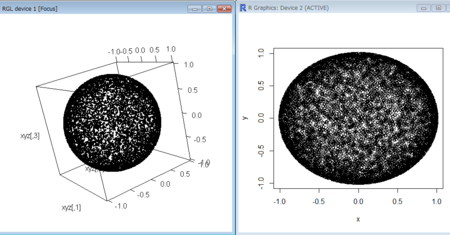
２変数が、３次元球面上のランダムな現象の２軸への射影であるとき

xyz<-matrix(rnorm(N*3),ncol=3)
xyz<-xyz/sqrt(apply(xyz^2,1,sum))
x<-xyz[,1]
y<-xyz[,2]
plot(x,y)
library(rgl)
plot3d(xyz)
cor(x,y)

> cor(x,y)
[1] -0.0006613149

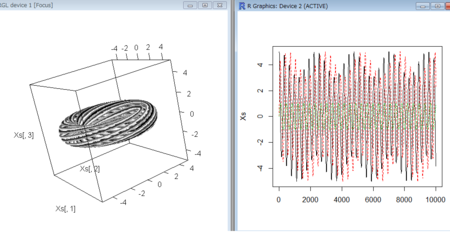
３変数の相互作用は球面とは限らなくて、トーラス上をアトラクタとした状態かもしれない。２変数がその３変数の関係の２つであるとき
- 「安定な状態」としてのアトラクタについてはこちら
- トーラス上の周回軌道を描くための関数MultDimTorus3()はこちら

# 普通にトーラス
incrRatio<-4
# 主要な輪は３回まわって元に戻る
# ２つの輪の周期が無理数だと、元に戻らないので、ぐるぐる回る
# 無理数としてpiとexpをとる
Ps<-c(pi,exp(1)) 
t<-seq(from=0,to=10,length.out=n)*2*pi

Xs<-matrix(0,length(t),k+1)
for(i in 1:length(t)){
	Xs[i,]<-MultDimTorus3(t[i]*Ps,incrRatio)
}
xlim<-ylim<-zlim<-c(min(Xs),max(Xs))

plot3d(Xs[,1],Xs[,2],Xs[,3],cex=0.1,col=gray((1:length(t))/length(t)),xlim=xlim,ylim=ylim,zlim=zlim)

plot(as.data.frame(Xs))
matplot(Xs,type="l")
cor(Xs[,1],Xs[,2])

> cor(Xs[,1],Xs[,2])
[1] 0.00333455